原文链接
问题描述
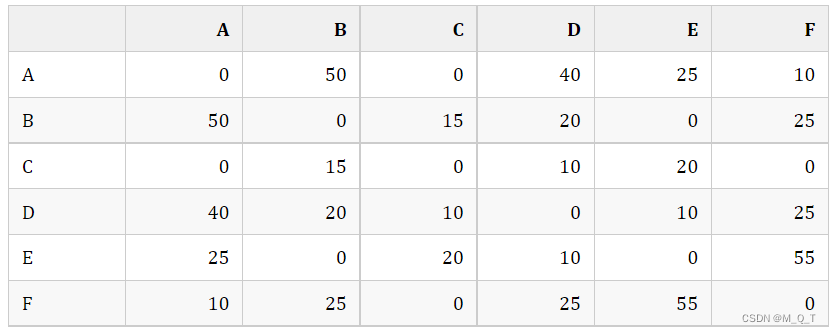
使用 Dijkstra 算法求图中的任意顶点到其它顶点的最短路径(求出需要经过那些点以及最短距离)。
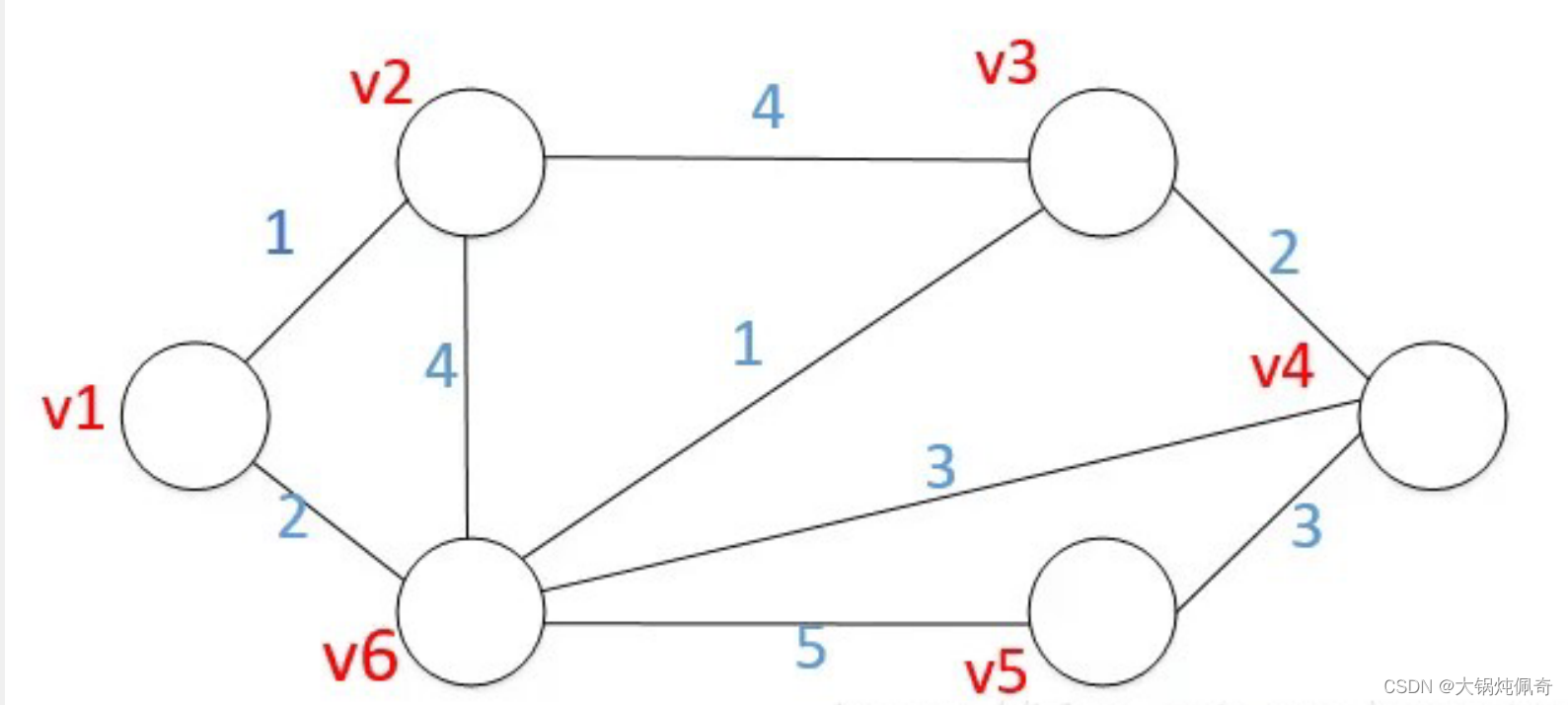
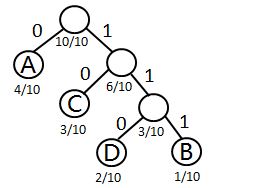
以下图为例:

算法思想
可以使用二维数组来存储顶点之间边的关系

首先需要用一个一维数组 dis 来存储 初始顶点到其余各个顶点的初始路程,以求 1 顶点到其它各个顶点为例:

将此时 dis 数组中的值称为最短路的“估计值”。
既然是求 1 号顶点到其余各个顶点的最短路程,那就先找一个离 1 号顶点最近的顶点。通过数组 dis 可知当前离 1 号顶点最近是 2 号顶点。当选择了 2 号顶点后,dis[2] 的值就已经从“估计值”变为了“确定值”,即 1 号顶点到 2 号顶点的最短路程就是当前 dis[2]值。为什么呢?因为目前离 1 号顶点最近的是 2 号顶点,并且这个图所有的边都是正数,那么肯定不可能通过第三个顶点中转,使得 1 号顶点到 2 号顶点的路程进一步缩短了。
既然选了 2 号顶点,接下来再来看 2 号顶点有哪些出边。有 2->3 和 2->4 这两条边。先讨论通过 2->3 这条边能否让 1 号顶点到 3 号顶点的路程变短。也就是说现在比较 dis[3] 和 dis[2] + G[2][3]的大小。其中 dis[3] 表示 1 号顶点到 3 号顶点的路程。dis[2] + G[2][3] 中 dis[2] 表示 1 号顶点到 2 号顶点的路程,G[2][3] 表示 2->3 这条边。所以 dis[2] + G[2][3] 就表示从 1 号顶点先到 2 号顶点,再通过 2->3 这条边,到达 3 号顶点的路程。
在本例中 dis[3] = 12,dis[2] + G[2][3] = 1 + 9 = 10,dis[3] > dis[2] + G[2][3],所以 dis[3] 要更新为 10。这个过程有个专业术语叫做“松弛”。即 1 号顶点到 3 号顶点的路程即 dis[3],通过 2->3 这条边松弛成功。这是 Dijkstra 算法的主要思想:通过“边”来松弛初始顶点到其余各个顶点的路程。
同理通过 2->4(G[2][4]),可以将 dis[4]的值从 ∞ 松弛为 4(dis[4] 初始为 ∞,dis[2] + G[2][4] = 1 + 3 = 4,dis[4] > dis[2] + G[2][4],所以 dis[4] 要更新为 4)。
刚才对 2 号顶点所有的出边进行了松弛。松弛完毕之后 dis 数组为:

接下来,继续在剩下的 3、4、5 和 6 号顶点中,选出离 1 号顶点最近的顶点。通过上面更新过 dis 数组,当前离 1 号顶点最近是 4 号顶点。此时,dis[4] 的值已经从“估计值”变为了“确定值”。下面继续对 4 号顶点的所有出边(4->3,4->5 和 4->6)用刚才的方法进行松弛。松弛完毕之后 dis 数组为:

继续在剩下的 3、5 和 6 号顶点中,选出离 1 号顶点最近的顶点,这次选择 3 号顶点。此时,dis[3] 的值已经从“估计值”变为了“确定值”。对 3 号顶点的所有出边(3->5)进行松弛。松弛完毕之后 dis 数组为:

继续在剩下的 5 和 6 号顶点中,选出离 1 号顶点最近的顶点,这次选择 5 号顶点。此时,dis[5] 的值已经从“估计值”变为了“确定值”。对5号顶点的所有出边(5->4)进行松弛。松弛完毕之后 dis 数组为:

最后对 6 号顶点所有点出边进行松弛。因为这个例子中 6 号顶点没有出边,因此不用处理。到此,dis 数组中所有的值都已经从“估计值”变为了“确定值”。
最终 dis 数组如下,这便是 1 号顶点到其余各个顶点的最短路径。

总结一下刚才的算法。算法的基本思想是:每次找到离源点(上面例子的源点就是 1 号顶点)最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。基本步骤如下:
将所有的顶点分为两部分:已知最短路程的顶点集合 P 和未知最短路径的顶点集合 Q。最开始,已知最短路径的顶点集合 P 中只有源点一个顶点。这里用一个 visited[ i ]数组来记录哪些点在集合 P 中。例如对于某个顶点 i,如果 visited[ i ]为 1 则表示这个顶点在集合 P 中,如果 visited[ i ]为 0 则表示这个顶点在集合 Q 中;
设置源点 s 到自己的最短路径为 0 即 dis = 0。若存在源点有能直接到达的顶点 i,则把 dis[ i ]设为 G[s][ i ]。同时把所有其它(源点不能直接到达的)顶点的最短路径为设为 ∞;
在集合 Q 的所有顶点中选择一个离源点 s 最近的顶点 u(即 dis[u] 最小)加入到集合 P。并考察所有以点 u 为起点的边,对每一条边进行松弛操作。例如存在一条从 u 到 v 的边,那么可以通过将边 u->v 添加到尾部来拓展一条从 s 到 v 的路径,这条路径的长度是 dis[u] + G[u][v]。如果这个值比目前已知的 dis[v] 的值要小,我们可以用新值来替代当前 dis[v] 中的值;
重复第 3 步,如果集合 Q 为空,算法结束。最终 dis 数组中的值就是源点到所有顶点的最短路径
注意
Dijkstra 算法不能应用于有负权重的图
Dijkstra 时间复杂度为 O(N2)
Python 实现
def Dijkstra(G, start):# 输入是从 0 开始,所以起始点减 1start = start - 1inf = float('inf')node_num = len(G)# visited 代表哪些顶点加入过visited = [0] * node_num# 初始顶点到其余顶点的距离dis = {node: G[start][node] for node in range(node_num)}# parents 代表最终求出最短路径后,每个顶点的上一个顶点是谁,初始化为 -1,代表无上一个顶点parents = {node: -1 for node in range(node_num)}# 起始点加入进 visited 数组visited[start] = 1# 最开始的上一个顶点为初始顶点last_point = startfor i in range(node_num - 1):# 求出 dis 中未加入 visited 数组的最短距离和顶点min_dis = inffor j in range(node_num):if visited[j] == 0 and dis[j] < min_dis:min_dis = dis[j]# 把该顶点做为下次遍历的上一个顶点last_point = j# 最短顶点假加入 visited 数组visited[last_point] = 1# 对首次循环做特殊处理,不然在首次循环时会没法求出该点的上一个顶点if i == 0:parents[last_point] = start + 1for k in range(node_num):if G[last_point][k] < inf and dis[k] > dis[last_point] + G[last_point][k]:# 如果有更短的路径,更新 dis 和 记录 parentsdis[k] = dis[last_point] + G[last_point][k]parents[k] = last_point + 1# 因为从 0 开始,最后把顶点都加 1return {key + 1: values for key, values in dis.items()}, {key + 1: values for key, values in parents.items()}if __name__ == '__main__':inf = float('inf')G = [[0, 1, 12, inf, inf, inf],[inf, 0, 9, 3, inf, inf],[inf, inf, 0, inf, 5, inf],[inf, inf, 4, 0, 13, 15],[inf, inf, inf, inf, 0, 4],[inf, inf, inf, inf, inf, 0]]dis, parents = Dijkstra(G, 1)print("dis: ", dis)print("parents: ", parents)
输出为
dis: {1: 0, 2: 1, 3: 8, 4: 4, 5: 13, 6: 17}
parents: {1: -1, 2: 1, 3: 4, 4: 2, 5: 3, 6: 5}
如果求 1 号顶点到 6 号顶点的最短距离,dis[6] = 17,所以最短距离为 17。
再看 parents[6] = 5,说明 6 号顶点的上一个顶点为 5,parents[5] = 3,说明 5 号顶点的上一个顶点为 3,以此类推,最终 1 号顶点到 6 号顶点的路径为 1->2->4->3->5->6。
优化思路
其中每次找到离 1 号顶点最近的顶点的时间复杂度是 O(N),可以用“堆”来优化,使得这一部分的时间复杂度降低到 O(logN);
另外对于边数 M 少于 N2 的稀疏图来说(把 M 远小于 N2 的图称为稀疏图,而 M 相对较大的图称为稠密图),可以用邻接表来代替邻接矩阵,使得整个时间复杂度优化到 O((M+N)logN)。注意,在最坏的情况下 M 就是 N2,这样的话 MlogN 要比 N2 还要大。但是大多数情况下并不会有那么多边,所以 (M+N)logN 要比 N2 小很多