本文总结了图的几种最短路径算法的实现:深度或广度优先搜索算法,费罗伊德算法,迪杰斯特拉算法,Bellman-Ford 算法。
1)深度或广度优先搜索算法(解决单源最短路径)
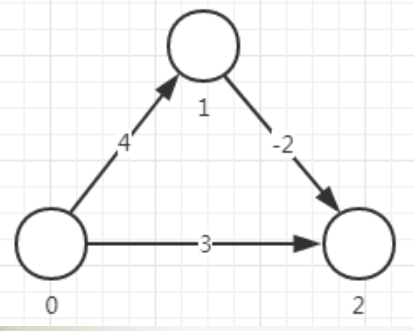
从起点开始访问所有深度遍历路径或广度优先路径,则到达终点节点的路径有多条,取其中路径权值最短的一条则为最短路径。
下面是核心代码:
void dfs(int cur,int dst){if(minpath<dst) return;//当前走过的路径大雨之前的最短路径,没有必要再走下去了if(cur==en){//临界条件,当走到终点nif(minpath>dst){minpath=dst;return;}}for(int i=1;i<=n;i++){if(mark[i]==0&&edge[cur][i]!=inf&&edge[cur][i]!=0){mark[i]=1;dfs(i,dst+edge[cur][i]);mark[i]=0;//需要在深度遍历返回时将访问标志置0}}return;
}例:先输入n个节点,m条边,之后输入有向图的m条边,边的前两个元素表示起点和终点,第三个值表示权值,输出1号城市到n号城市的最短距离。
#include<bits/stdc++.h>
using namespace std;
#define nmax 110
#define inf 999999999
int minpath,n,m,en,edge[nmax][nmax],mark[nmax];//最短路径,节点数,边数,终点,邻接矩阵,节点访问标记
void dfs(int cur,int dst){if(minpath<dst) return;//当前走过的路径大雨之前的最短路径,没有必要再走下去了if(cur==en){//临界条件,当走到终点nif(minpath>dst){minpath=dst;return;}}for(int i=1;i<=n;i++){if(mark[i]==0&&edge[cur][i]!=inf&&edge[cur][i]!=0){mark[i]=1;dfs(i,dst+edge[cur][i]);mark[i]=0;//需要在深度遍历返回时将访问标志置0}}return;
}
int main ()
{while(cin>>n>>m&&n!=0){//初始化邻接矩阵for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){edge[i][j]=inf;}edge[i][i]=0;}int a,b;while(m--){cin>>a>>b;cin>>edge[a][b];}minpath=inf;memset(mark,0,sizeof(mark));mark[1]=1;en=n;dfs(1,0);cout<<minpath<<endl;}
}
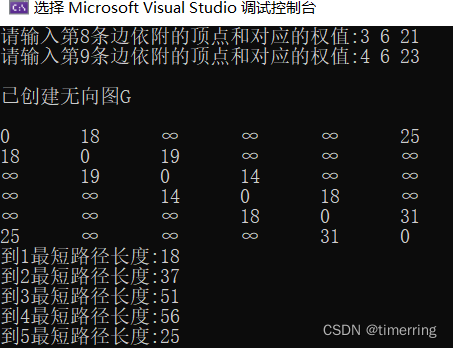
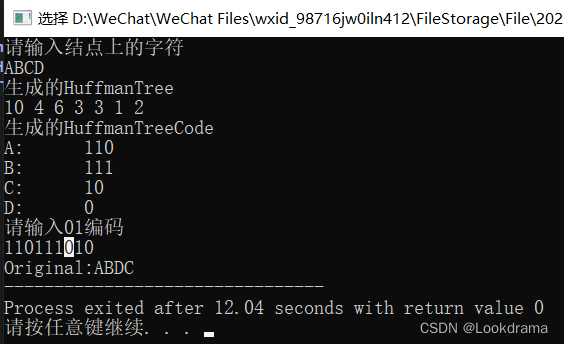
程序运行结果如下:
2)弗洛伊德算法(解决多源最短路径):时间复杂度o(n^3),空间复杂度o(n^2)
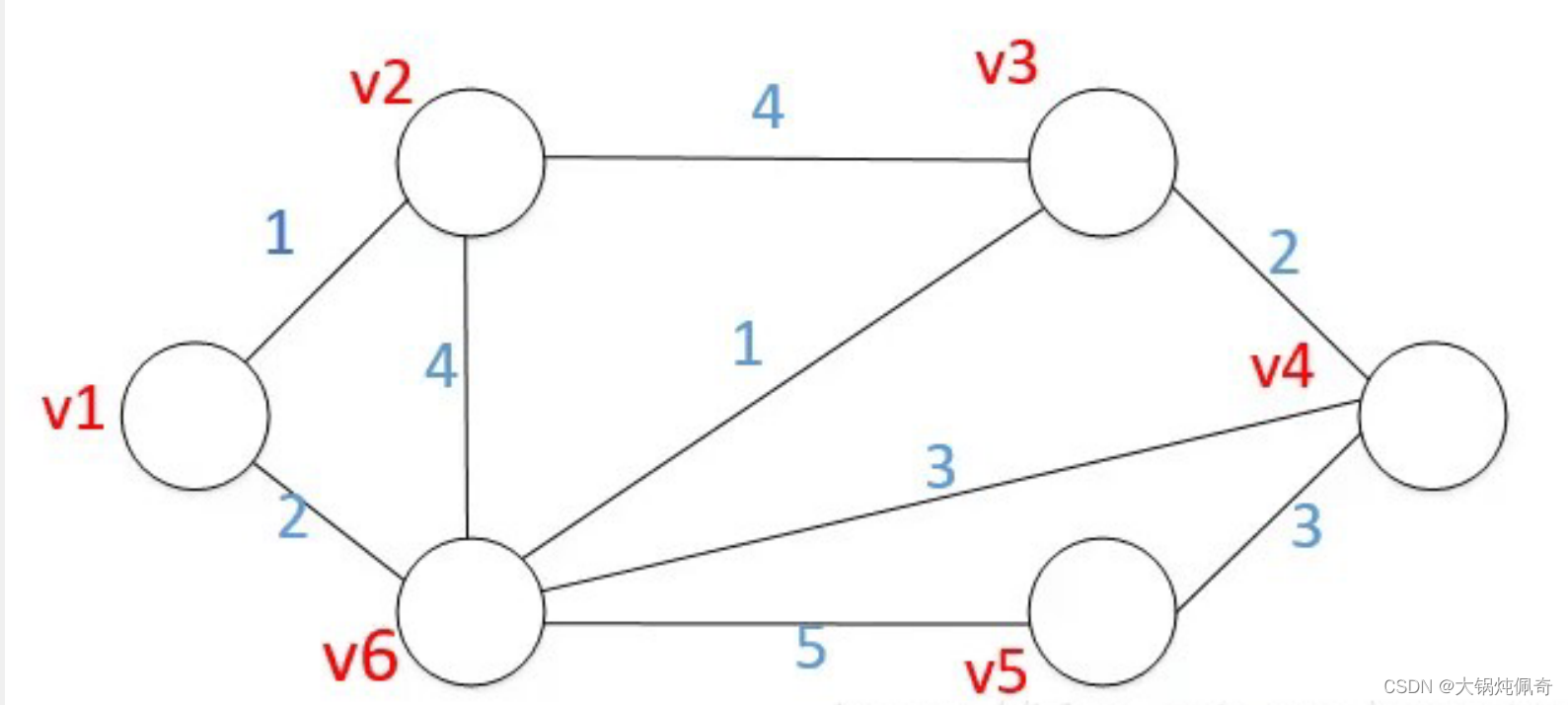
基本思想:最开始只允许经过1号顶点进行中转,接下来只允许经过1号和2号顶点进行中转.......允许经过1~n号所有顶点进行中转,来不断动态更新任意两点之间的最短距离。即求从i号顶点到j顶点只经过前k号点的最短距离。
分析如下:1,首先构建邻接矩阵