一 、目的：

1.掌握最短路径算法的基本原理及编程实现；

二 、环境：

operating system version：Win11
CPU instruction set:  x64
Integrated Development Environment：Viusal Studio 2022

三 、内容：

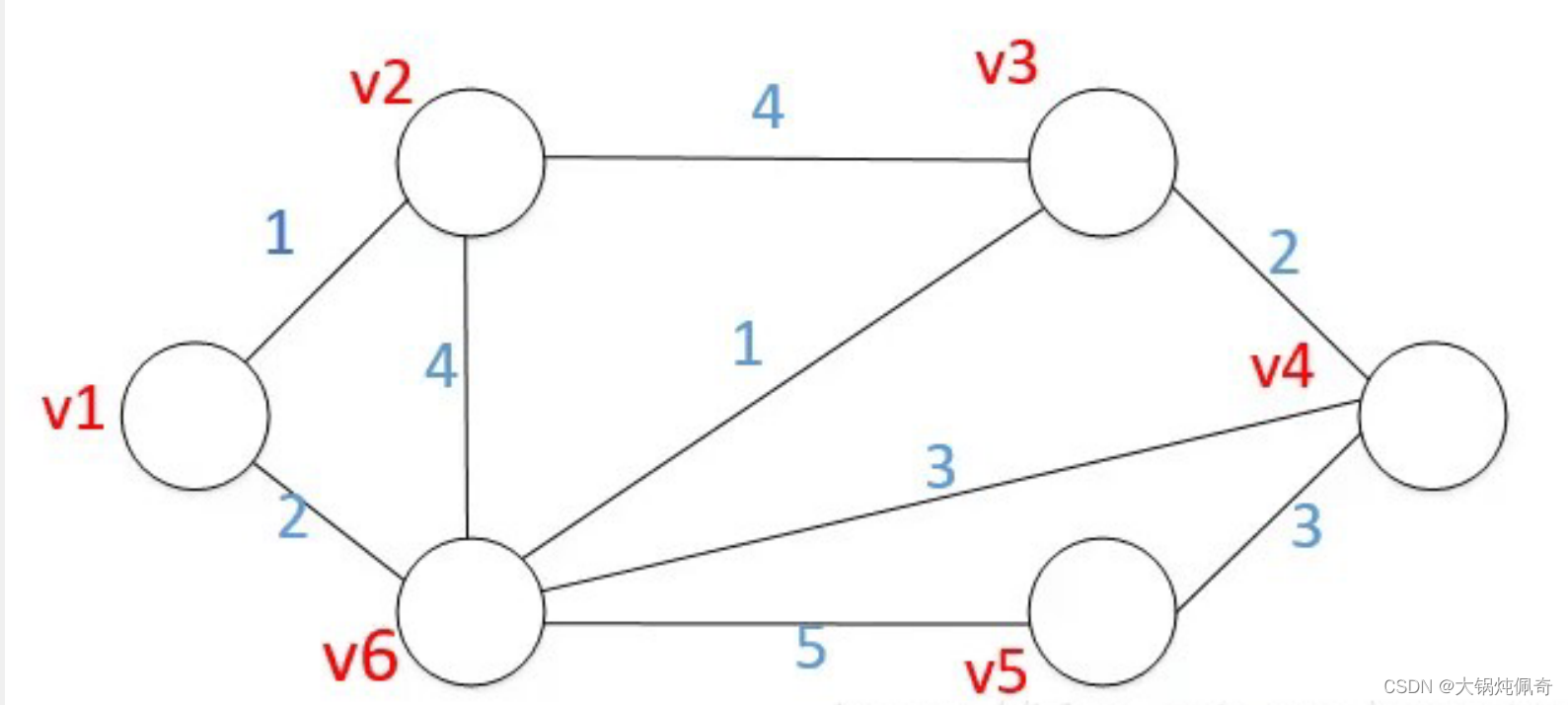
1)建立一张图，选择一种存储结构(邻接矩阵或邻接表)初始化该图；
2)用Dijkstra算法实现点与点之间的最短路径。

四 、要求：

1) 实现图的两种表示方法；
2) 实现Dijkstra算法；

五 、步骤：

1. 程序：
 

#include<iostream>  
#define MVNum 100  
#define MaxInt 32767 //极大值，即∞  
using namespace std;  
typedef int ArcType;  
typedef char VerTextType[20];  
int* D = new int[MVNum];  
bool* S = new bool[MVNum];   
int* Path = new int[MVNum];   
typedef struct ArcNode //边结点  
{  int adjver; //该边所指向的顶点位置  struct ArcNode* nextarc; //指向下一条边的指针  ArcType   weight;  
} ArcNode;  typedef struct VNode //顶点信息  
{  VerTextType data;  ArcNode* firstarc;  
} VNode, AdjList[MVNum];  typedef struct node  
{  AdjList vertices;  int     vexnum; //图的当前顶点数  int     arcnum; //图的当前边数  
} ALGraph;  //临接表存储方式最短路径（dijkstra）,复杂度O(n^2)  
void ShortestPath_DIJ2(ALGraph G, int v0, ArcType D[], int Path[])  
{  int ok[MVNum], i, j; // ok数组标记是否确定最短路径  for (i = 0; i < G.vexnum; i++) {  ok[i] = 0;  Path[i] = -1;  D[i] = MaxInt;  }  D[v0] = 0;  for (i = 0; i < G.vexnum; i++) {  int min_node = -1;  for (j = 0; j < G.vexnum; j++) {  if (ok[j] == 0 && (min_node == -1 || D[j] < D[min_node])) {  min_node = j;  }  }  if (min_node == -1) break;  ok[min_node] = 1;  ArcNode* cur = G.vertices[min_node].firstarc;  while (cur != NULL) {  if (ok[cur->adjver] == 0 && D[cur->adjver] > D[min_node] + cur->weight) {  D[cur->adjver] = D[min_node] + cur->weight;  Path[cur->adjver] = min_node;  }  cur = cur->nextarc;  }  }  }  //图的邻接矩阵  
typedef struct  
{  char vexs[MVNum];                        //顶点表   int arcs[MVNum][MVNum];                 //邻接矩阵  
}Graph;  void InitGraph(Graph& G, int vex)  
{  cout << "输入点的名称，如a" << endl;  for (int i = 0; i < vex; ++i) {  cout << "请输入第" << (i + 1) << "个点的名称:";  cin >> G.vexs[i];                                       }  cout << endl;  for (int i = 0; i < vex; ++i)  //初始化邻接矩阵，边的权值均置为极大值MaxInt   for (int j = 0; j < vex; ++j)  {  if (j != i)  G.arcs[i][j] = MaxInt;  else  G.arcs[i][j] = 0;  }  
}  //确定点v在G中的位置  
int LocateVex(Graph G, char v, int vex) {  for (int i = 0; i < vex; ++i)  if (G.vexs[i] == v)  return i;  return -1;  
}  //创建无向网G  
void CreateUDN(Graph& G, int vex, int arc)  
{  int i, j, k;  cout << "输入边依附的顶点(node1 node2 weight)" << endl;  for (k = 0; k < arc; ++k) {  //构造邻接矩阵   char v1, v2;  int o;  cout << "请输入第" << (k + 1) << "条边依附的顶点和对应的权值:";  cin >> v1 >> v2 >> o;                                       i = LocateVex(G, v1, vex);  j = LocateVex(G, v2, vex);            G.arcs[j][i] = G.arcs[i][j] = o;                          }  
}  void DisplayGraph(Graph G, int vex)  
{  int i, j;  for (i = 0; i < vex; ++i) {  for (j = 0; j < vex; ++j) {  if (G.arcs[i][j] != MaxInt)  cout << G.arcs[i][j] << "\t";  else  cout << "∞" << "\t";  }  cout << endl;  }  
}  //用Dijkstra算法求无向网G的v0顶点到其余顶点的最短路径   
void ShortestPath_DIJ(Graph G, int v0, int vex) {  int v, i, w, min;  int n = vex;   for (v = 0; v < n; ++v) {                                  S[v] = false;                                         D[v] = G.arcs[v0][v];                                 if (D[v] < MaxInt)  Path[v] = v0;                      else Path[v] = -1;                                    }  S[v0] = true;   D[v0] = 0;  for (i = 1; i < n; ++i) {                                      min = MaxInt;  for (w = 0; w < n; ++w)  if (!S[w] && D[w] < min) {                         v = w;  min = D[w];  }//if             S[v] = true;                                      for (w = 0; w < n; ++w)                              //更新从v0出发到集合V?S上所有顶点的最短路径长度   if (!S[w] && (D[v] + G.arcs[v][w] < D[w])) {  D[w] = D[v] + G.arcs[v][w];                 //更新D[w]   Path[w] = v;                                //更改w的前驱  }  }  for (int i = 0; i < vex; i++) {  if (D[i] != 0)  if (D[i] != MaxInt)  cout << "到" << G.vexs[i] << "最短路径长度:" << D[i] << endl;  else  {  cout << "到" << G.vexs[i] << "最短路径长度:" << "无法到达" << endl;  }  }  
}  int main()  
{  Graph G;  int vexnum, arcnum;   cout << "请分别输入总顶点数和总边数:";  cin >> vexnum >> arcnum;  cout << endl;  InitGraph(G, vexnum);  int v = 0;  CreateUDN(G, vexnum, arcnum);  cout << endl;  cout << "已创建无向图G" << endl << endl;  DisplayGraph(G, vexnum);  int v0 = LocateVex(G, '0', vexnum);  ShortestPath_DIJ(G, v0, vexnum);  
}

2.程序结果：

1）程序运行，我使用的测试数据如下所示：

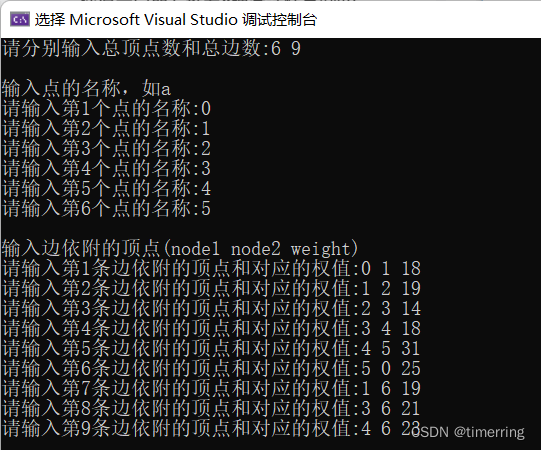
2）我采用邻接矩阵的方式实现最短路径的存储。创建的无向图G如下：

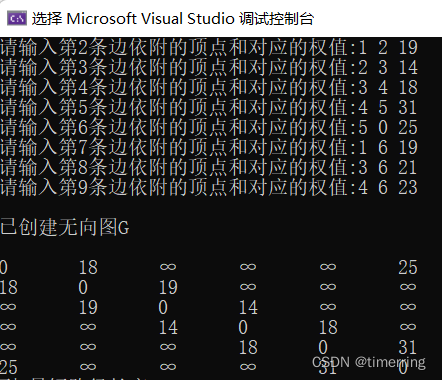
3）最终通过Dijkstra算法输出源点0到其余节点的最短路径如下：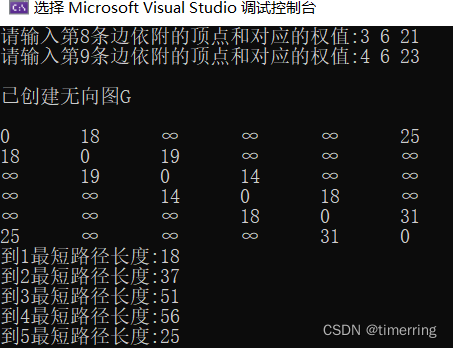

六 、小结：

       此次是关于Dijkstra最短路径算法的编程与实现。我先分别尝试了采用邻接矩阵以及邻接表的存储结构，比较了他们的优缺点：其中图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（邻接矩阵）存储图中的边或弧的信息。从这个矩阵中，可以较容易知道图中的信息。1）可以判断任意两顶点是否有边无边；2）可以知道某个顶点的度，其实就是这个顶点vi在邻接矩阵中第i行或（第i列）的元素之和；3）求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍，arc[i][j]为1就是邻接点；而邻接表则是将图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储。图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以，用单链表存储，无向图称为顶点vi的边表，有向图则称为顶点vi作为弧尾的出边表。

        最终我在构建图的时候选择了邻接矩阵的方式实现。通过邻接矩阵的Dijkstra时间复杂度是O(N2)。其中每次找到离1号顶点最近的顶点的时间复杂度是 O(N)。整个程序的基本思想是：设置两个顶点集S和T，集合S中存放已经找到最短路径的顶点，集合T中存放着当前还未找到最短路径的顶点；初始状态下，集合S中只包含源点V1，T中为除了源点以外的其他顶点，此时源点到各顶点的最短路径为两个顶点所连的边上的权值，若是源点V1到该顶点没有边，则最小路径为无穷大；从集合T中选取到源点V1的路径长度最短的顶点Vi加入到集合S中；修改源点V1到集合T中剩余顶点Vj的最短路径长度。新的最短路径长度值为Vj原来的最短路径长度值与顶点Vi的最短路径长度加上Vi到Vj的路径长度值中的较小者；不断重复步骤三、4，直至集合T的顶点所有加入到集合S中。