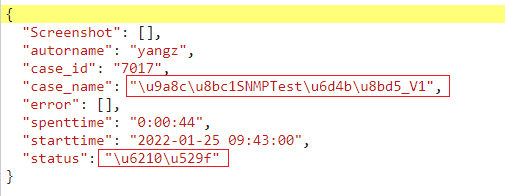
Python中hmmlearn给出了三种HMM模型：MultiomialHMM,GaussianHMM,GMMHMM。本文以MultiomialHMM为例，使用《从机器学习到深度学习》中第六章的活动/天气模型进行推算。

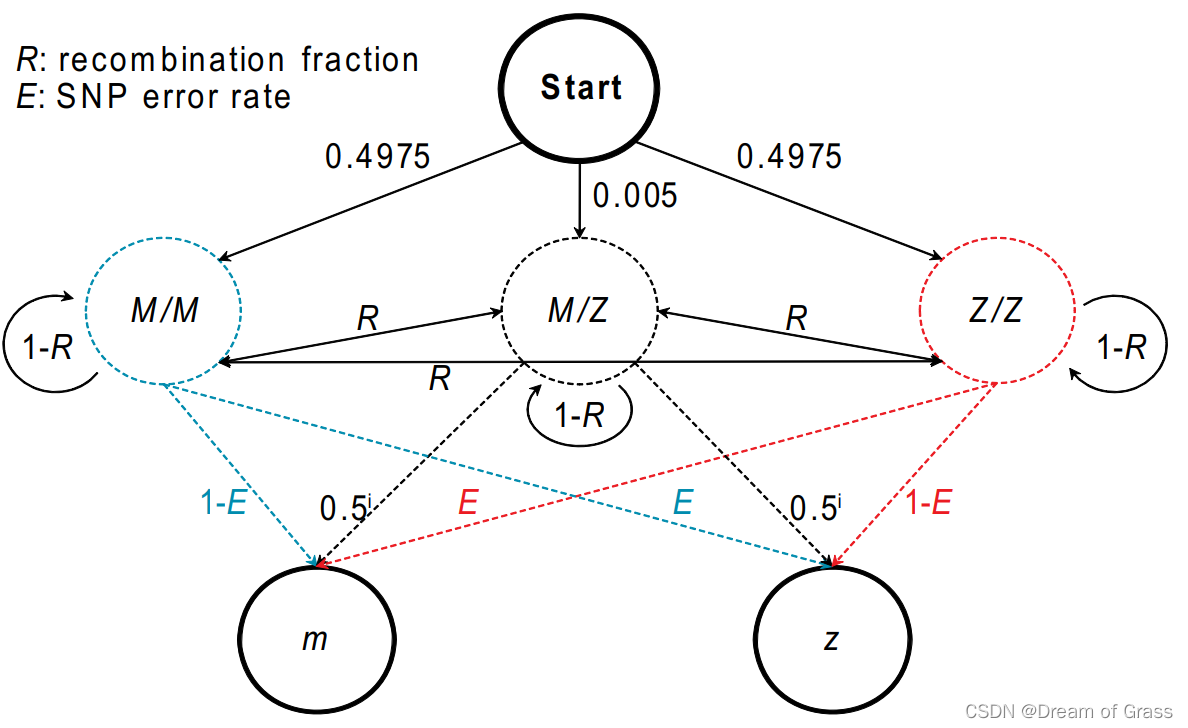
       假设有这样一个问题，远在另一个城市上大学的儿子每天通过邮件向你汇报他今天做的最多事情是什么，这些事情可能是这三项之一：打球、读书、访友。那么在这种场景下，如何推测儿子所在城市的天气情况。假设儿子活动有如下规律：在晴天更可能打球，在阴天更可能访友，在雨天更可能的读书，在散发概率矩阵中显示为概率值大小。

       在这个问题中，儿子的活动类型构成了模型的可见层，天气情况成了隐藏层。

       那么 1.状态的样本空间 states = ('晴', '阴','雨')；

               2.起始个状态概率  start_probability = {'晴':0.5, '阴':0.3,'雨':0.2}
               3.状态转移概率     transition_probability = {
                                                                                    '晴': {'晴':0.7, '阴':0.2,'雨':0.1},
                                                                                     '阴': {'晴':0.3, '阴':0.5,'雨':0.2},
                                                                                     '雨': {'晴':0.3, '阴':0.4,'雨':0.3},
                                                                                   }
                4.状态->观测的发散概率  emission_probability = {
                                                                                     '晴': { '读书': 0.3,'打球': 0.4, '访友': 0.3},
                                                                                     '阴': { '读书': 0.3,'打球': 0.2, '访友': 0.5},
                                                                                     '雨': { '读书': 0.8,'打球': 0.1, '访友': 0.1},
                                                                                   }

                 5.观测的样本空间 observations = ( '读书', '打球','访友','读书')

则MultiomialHMM代码如下：

import numpy as np
from hmmlearn import hmmstates = ['晴', '阴','雨']
n_states = len(states)observations = ['读书', '打球','访友','读书']
n_observations = len(observations)start_probability = np.array([0.5, 0.3, 0.2])transition_probability = np.array([[0.7, 0.2, 0.1],[0.3, 0.5, 0.2],[0.3, 0.4, 0.3]
])emission_probability = np.array([[0.3, 0.4, 0.3],[0.3, 0.2, 0.5],[0.8, 0.1, 0.1]
])model = hmm.MultinomialHMM(n_components=n_states)
model.startprob_=start_probability
model.transmat_=transition_probability
model.emissionprob_=emission_probability
print(model.startprob_)
print(model.transmat_)
print(model.emissionprob_)
observe_chain=np.array([0,1,2,0]).reshape(-1,1)
print(model.score(observe_chain))
print(model.predict(observe_chain))

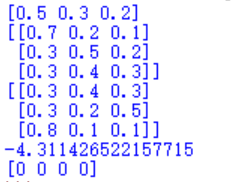
结果如下：

 第一行为初始概率，第二至四行为转移概率矩阵，第五至七行为emission概率，-4.31142为打分，[0000]为预测结果。接下来用维特比算法计算隐藏状态链，即HMM模型的解码问题。

---

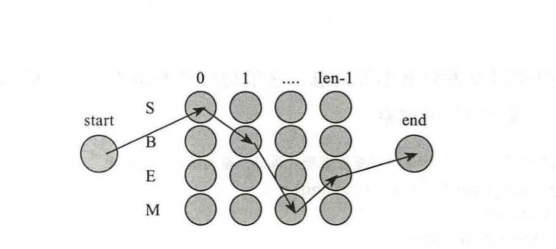
维特比算法用来在给定HMM模型参数和一个可见状态链时，找出最可能的隐藏状态链。

维特比算法的过程可分为两步：

1.正方向推算：用动态规划的方法从第一个隐藏结点开始逐步计算每个可能状态；

2.反方向推理：计算到最后一个结点时，概率最大的那个状态就是最后一个隐藏结点的被推测状态。

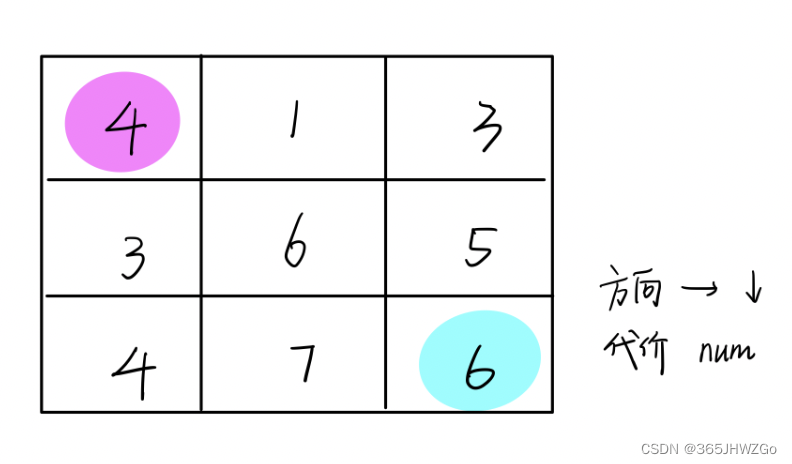
       则计算由下图所示：

第四天结果没算，则前三天应该为雨、晴、晴，对应概率为0.16,0.042,0.0082。书本中给出最终结果为[晴 晴 晴 晴]，与计算有出入，于是我找了一段代码进行验算。

python代码实现如下 （原代码https://blog.csdn.net/zhangduan8785/article/details/80443650）

import math
# 状态的样本空间
states = ('晴', '阴','雨')
# 观测的样本空间
observations = ( '读书', '打球','访友','读书')
# 起始个状态概率
start_probability = {'晴':0.5, '阴':0.3,'雨':0.2}
# 状态转移概率
transition_probability = {'晴': {'晴':0.7, '阴':0.2,'雨':0.1},'阴': {'晴':0.3, '阴':0.5,'雨':0.2},'雨': {'晴':0.3, '阴':0.4,'雨':0.3},
}
# 状态->观测的发散概率
emission_probability = {'晴': { '读书': 0.3,'打球': 0.4, '访友': 0.3},'阴': { '读书': 0.3,'打球': 0.2, '访友': 0.5},'雨': { '读书': 0.8,'打球': 0.1, '访友': 0.1},
}
# 计算以E为底的幂
def E(x):#return math.pow(math.e,x)return xdef display_result(observations,result_m):"""较为友好清晰的显示结果:param result_m::return:"""# 从结果中找出最佳路径#print(result_m)infered_states = []final = len(result_m) - 1(p, pre_state), final_state = max(zip(result_m[final].values(), result_m[final].keys()))infered_states.insert(0, final_state)infered_states.insert(0, pre_state)for t in range(final - 1, 0, -1):_, pre_state = result_m[t][pre_state]infered_states.insert(0, pre_state)print(format("Viterbi Result", "=^59s"))head = format("obs", " ^10s")head += format("Infered state", " ^18s")for s in states:head += format(s, " ^15s")print(head)print(format("", "-^59s"))for obs,result,infered_state in zip(observations,result_m,infered_states):item = format(obs," ^10s")item += format(infered_state," ^18s")for s in states:item += format(result[s][0]," >12.8f")if infered_state == s:item += "(*)"else:item +="   "print(item)print(format("", "=^59s"))def viterbi(obs, states, start_p, trans_p, emit_p):result_m = [{}] # 存放结果,每一个元素是一个字典，每一个字典的形式是 state:(p,pre_state)# 其中state,p分别是当前状态下的概率值，pre_state表示该值由上一次的那个状态计算得到for s in states:  # 对于每一个状态result_m[0][s] = (E(start_p[s]*emit_p[s][obs[0]]),None) # 把第一个观测节点对应的各状态值计算出来#print('11',result_m[0][s])for t in range(1,len(obs)):result_m.append({})  # 准备t时刻的结果存放字典，形式同上for s in states: # 对于每一个t时刻状态s,获取t-1时刻每个状态s0的p,结合由s0转化为s的转移概率和s状态至obs的发散概率# 计算t时刻s状态的最大概率，并记录该概率的来源状态s0# max()内部比较的是一个tuple:(p,s0),max比较tuple内的第一个元素值result_m[t][s] = max([(E(result_m[t-1][s0][0]*trans_p[s0][s]*emit_p[s][obs[t]]),s0) for s0 in states])#print(result_m[t][s])return result_m    # 所有结果（包括最佳路径）都在这里，但直观的最佳路径还需要依此结果单独生成，在显示的时候生成def example():"""一个可以交互的示例"""result_m = viterbi(observations,states,start_probability,transition_probability,emission_probability)display_result(observations,result_m)while True:user_obs = input("轮到你来输入观测,计算机来推断可能状态\n""使用 'N' 代表'打球', 'C' 代表'读书','D'代表'访友'\n""您输入：('q'将退出):")if len(user_obs) ==0 or 'q' in user_obs or 'Q' in user_obs:breakelse:obs = []for o in user_obs:if o.upper() == 'N':obs.append("打球")elif o.upper() == 'C':obs.append("读书")elif o.upper() == 'D':obs.append("访友")else:passresult_m = viterbi(obs,states,start_probability,transition_probability,emission_probability)display_result(obs,result_m)if __name__ == "__main__":example()

结果：

实验结果与书本结果一直，计算结果也与我计算一致，但是第一天结果判断有出入：0.16大于0.15，却把可能判定为了0.15，这位同学的代码中还给出了一段交互代码，我观测CCCCCDDDDDDDNNN，这时第一天预测概率相同，却把可能性判定为0.16。这个疑问进行保留。 接下来我又观测了CCNNNNNDDDDDDDD，即第一天为读书，结果如下：

由概率可知前两天--雨天概率大于晴天，但都把结果判定为晴天，第八天开始，晴天概率都大于阴天，却判定为阴天。

观测NNDDDDCCCCCCC，即第一天为打球：

前两天判定结果与计算概率相同，但第三天到第九天结果却与判定不同。

如果修改初始概率为start_probability = {'晴':0.1, '阴':0.3,'雨':0.6}，则结果为：

第一二次观察结果与判定是一致的，但第三次中很显然第一天、第四天、第六天、第七天、第八天、第九天、第十天的判定与结果都不一致。

---

对于这个问题，是因viterbi算法是分两步，我们一直在用第一步前向计算，但是确定其判定结果是根据第二步反方向推理（计算到最后一个结点时，概率最大的那个状态就是最后一个隐藏结点的被推测状态）。所以，计算出某一天的天气分布概率，这并不能就说明概率高的就是当天的天气，要从最后一天向前推，也就是如下：