1. DSA 背景介绍

动态内存管理算法 DSA，Dynamic storage allocation。RTOS 一般情况下动态内存使用malloc申请分配，但是存在两个缺陷：

由于分配算法的复杂度，分配的时间不定；
在不断申请、释放的过程中，容易因为内存对齐而产生碎片化内存；

这两个缺陷在实时操作系统中是不允许的，所以操作系统必须提供一套有效、合理、时间可确定的动态内存管理机制。

既然传统malloc存在两个缺陷，那就抱着解决这两个缺陷的目的出发，去建立一套更适合于嵌入式系统的动态内存管理系统。目前有两种不同的解决方案：

动态内存堆管理算法（mmheap），用于不定长分配
静态内存池管理算法（mmblk），用于定长分配

1.1 mmheap

mmheap 一般采用 TLSF 算法。TLSF 全称 Two-Level Segregated Fit memory allocator，两级隔离Fit内存分配器，是一款通用的动态内存分配器，专门设计用于满足实时要求。tlsf source code。具有以下特点：

malloc，free，realloc，memalign的算法复杂度变为O(1)；
每次分配的开销极低（4字节）；
低碎片化
支持动态添加和删除内存池区域
TLSF主要采用两级位图(Two-Level Bitmap)与分级空闲块链表(Segregated Free List)的数据结构管理动态内存池(memory pool)以及其中的空闲块(free blocks)，用Good-Fit的策略进行分配。

需要注意：

TLSF算法分配速度不一定快，只是说能保证分配的时间是个常数（malloc不能保证）；
TLSF也叫多内存堆管理算法，支持动态增加或者删除多块不连续的内存，将它们作为一个内存堆使用；

1.2 mmblk

静态内存池就是将一块内存划分为n个大小相等的块，用户可以动态的申请、释放一个块，假装在使用动态内存。

在这里插入图片描述

2. TLSF 原理

2.1 存储结构

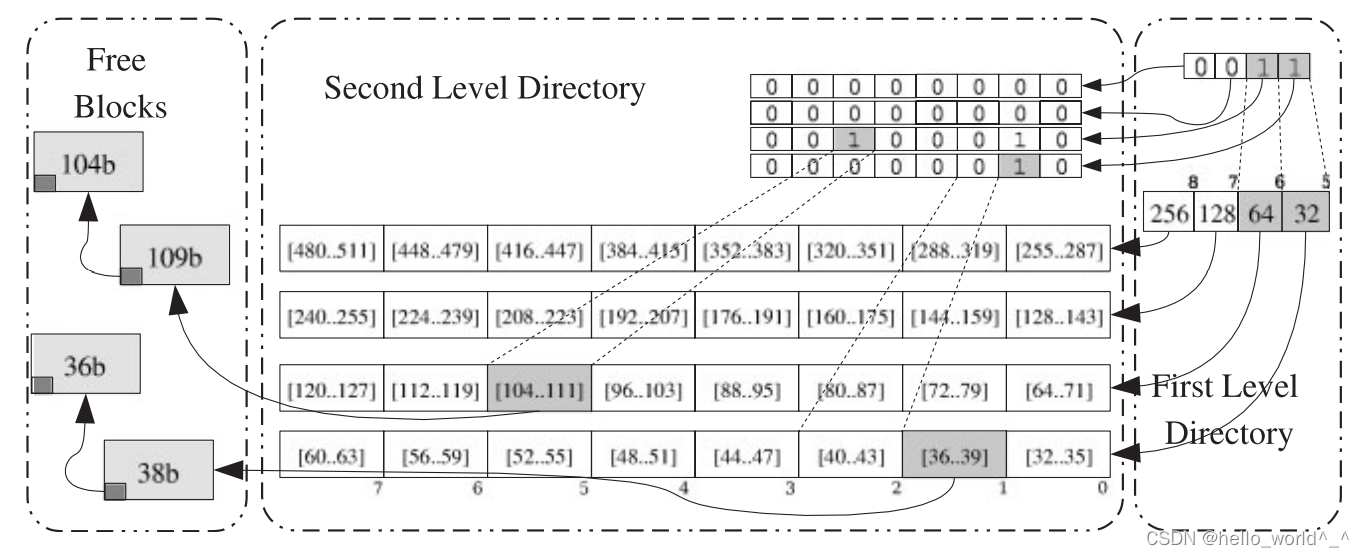
TLSF 采用两级链表的形式来加快查找：

第一级链表 First List (简称fl)。第一层将空闲内存块的大小根据2的幂进行分类，如（16、32、64…），第一级的索引值fli决定了这一级内存块的大小，范围为 [2^i,2(i+1)] ;第一级索引值计算：
fli = min( $log_{2}{(memorypoolsize)}$ , 31)
第二级链表 Second List (简称sl)。第二层链表在第一层的基础上，按照一定的间隔，线性分段，其范围应该在1-32，对于32bit的处理器，第二级的索引值sli一般为4或者5(经验值)。

在这里插入图片描述

例如上图分为fl和sl两级索引，FL_bitmap和SL_bitmaps[]的每个bit代表是否被使用：

fl分为8级。
sl分为4级。这里说明下，图中sl分了8个小区，我们计算sl时会将8个小区合为4个小区；

比如2的6次方这一段：

第一级的FL_bitmap为110...1..0,次高位为1，次高位对应着2的6次方这一段，说明这一段有空闲块。
第二级链表分为4个小区间[64,80），[80,96)，[96,112)，[112，128)，每一级的链表都有一个bitmap用于标记对应的链表中是否有内存块。SL_bitmap位00000010，其对应着[80,96)这个区间有空闲块，即下面的89 Byte。

通过两级索引来查找或释放内存，malloc与free的所有操作花费是个时间常数，时间响应复杂度都为O(1)；

2.2 内存池初始化

struct bhdr_struct

内存块的控制头，每个内存块不论是free 还是 malloc 状态都需要一个控制头：

typedef struct bhdr_struct {// prev_hdr 指向地址上连续的前一内存块，只有在当前内存状态为 malloc 时才有意义。// 主要在当前内存块释放时，判断前一内存块是否是 free 状态，是否可以合并。// 在内存释放时会同时判断是否能够和前后连续地址的内存块进行合并，为什么不多加一个指针指向地址上连续的后一内存块？// 这是因为后一个内存块地址可以根据自己的长度计算出来，而前一内存块地址是没法计算出来，这样就能节省一个指针的空间struct bhdr_struct *prev_hdr;// size 存储了剩余内存空间的大小，它是从后面的 ptr->buffer[0] 开始计算的// 因为 size 是 4字节对齐，所以最低两位用来做使用标识：// bit0表示当前块是否使用，bit1表示前一内存块是否被使用。(置0表示使用，1表示未使用)size_t size;union {// 在 malloc 状态下，这里是有效数据的开始u8_t buffer[1];// 在 free 状态下，这里用来存储 free list 指针// 注意这里 free_ptr 和前面 prev_hdr 的区别：// free_ptr 链接的是 free list，内存地址上是不连续的。把相同大小的 free 内存块链接到一起// prev_hdr 指示的是地址上连续的上一内存块，而不管内存块的状态，只有在释放时尝试合并时才判断状态struct free_ptr_struct free_ptr;} ptr;
} bhdr_t;/* free list 指针结构，只有在内存块 free 时有效 */
typedef struct free_ptr_struct {struct bhdr_struct *prev;struct bhdr_struct *next;
} free_ptr_t;

TLSF_struct

内存池的控制头，也支持多个内存池链接到一起：


typedef struct TLSF_struct {/* the TLSF's structure signature */// 内存池签名字段u32_t tlsf_signature;// 操作锁
#if TLSF_USE_LOCKSTLSF_MLOCK_T lock;
#endif// 统计计数
#if TLSF_STATISTIC/* These can not be calculated outside tlsf because we* do not know the sizes when freeing/reallocing memory. */size_t used_size;size_t max_size;
#endif/* A linked list holding all the existing areas */// 链接多内存池扩展指针，实际存储位置放在一个内存块中area_info_t *area_head;/* the first-level bitmap *//* This array should have a size of REAL_FLI bits */// 一级链表的 bitmapu32_t fl_bitmap;/* the second-level bitmap */// 二级链表的 bitmapu32_t sl_bitmap[REAL_FLI];// 空闲链表矩阵bhdr_t *matrix[REAL_FLI][MAX_SLI];
} tlsf_t;/* 用于连接多个内存池 */
typedef struct area_info_struct {// 指向当前内存池的末端内存块bhdr_t *end; // 指向下一个内存池，扩展内存struct area_info_struct *next; 
} area_info_t;

init_memory_pool()

size_t init_memory_pool(size_t mem_pool_size, void *mem_pool)
{tlsf_t *tlsf;bhdr_t *b, *ib;/* (1.1) 参数合法值判断 */if (!mem_pool || !mem_pool_size || mem_pool_size < sizeof(tlsf_t) + BHDR_OVERHEAD * 8) {ERROR_MSG("init_memory_pool (): memory_pool invalid\n");return -1;}/* (1.2) 传入起始地址是否对齐判断 */if (((unsigned long) mem_pool & PTR_MASK)) {ERROR_MSG("init_memory_pool (): mem_pool must be aligned to a word\n");return -1;}/* (1.3) 防止重复初始化内存池 */tlsf = (tlsf_t *) mem_pool;/* Check if already initialised 此内存池已经初始化了*/if (tlsf->tlsf_signature == TLSF_SIGNATURE) {mp = mem_pool;b = GET_NEXT_BLOCK(mp, ROUNDUP_SIZE(sizeof(tlsf_t)));return b->size & BLOCK_SIZE;}mp = mem_pool;/* Zeroing the memory pool *//* (2.1) 对内存池所有空间清零 */memset(mem_pool, 0, sizeof(tlsf_t)); /* (2.2) 合法签名 */tlsf->tlsf_signature = TLSF_SIGNATURE;/* (2.3) 锁初始化 */TLSF_CREATE_LOCK(&tlsf->lock);/* (3) 初始化内存池中 struct TLSF_struct 结构以后的空间  */ib = process_area(GET_NEXT_BLOCK(mem_pool, ROUNDUP_SIZE(sizeof(tlsf_t))), ROUNDDOWN_SIZE(mem_pool_size - sizeof(tlsf_t)));/* (4) 根据返回结果，得到一块最大的内存 */b = GET_NEXT_BLOCK(ib->ptr.buffer, ib->size & BLOCK_SIZE);/* (5) 将最大一块内存 free 到内存池中，内存池就有内存可用了 */free_ex(b->ptr.buffer, tlsf); /* (6.1) 将 area_info_t * 指针指向实际的存储位置，内存池中第一个内存块 ib */tlsf->area_head = (area_info_t *) ib->ptr.buffer;/* (6.2) 更新统计 */
#if TLSF_STATISTICtlsf->used_size = mem_pool_size - (b->size & BLOCK_SIZE);tlsf->max_size = tlsf->used_size;
#endif/* (6.3) 返回内存池可用内存的长度 */return (b->size & BLOCK_SIZE);
}↓static __inline__ bhdr_t *process_area(void *area, size_t size)
{bhdr_t *b, *lb, *ib;area_info_t *ai;/* (3.1) 第一个内存块 ib，存储的是 area_info_t 结构。最后给 tlsf->area_head 指针使用*/ib = (bhdr_t *) area;ib->size =(sizeof(area_info_t) <MIN_BLOCK_SIZE) ? MIN_BLOCK_SIZE : ROUNDUP_SIZE(sizeof(area_info_t)) | USED_BLOCK | PREV_USED;/* (3.2) 第二个内存块 b，存储的是有效内存。当前是已分配状态，稍后释放给内存池*/b = (bhdr_t *) GET_NEXT_BLOCK(ib->ptr.buffer, ib->size & BLOCK_SIZE);b->size = ROUNDDOWN_SIZE(size - 3 * BHDR_OVERHEAD - (ib->size & BLOCK_SIZE)) | USED_BLOCK | PREV_USED;b->ptr.free_ptr.prev = b->ptr.free_ptr.next = 0;/* (3.3) 最后一个内存块 lb，存储的是一个结束标志。长度为0，没有任何有效数据*/lb = GET_NEXT_BLOCK(b->ptr.buffer, b->size & BLOCK_SIZE);lb->prev_hdr = b;lb->size = 0 | USED_BLOCK | PREV_FREE;/* (3.4) 第一个内存块 ib 数据区存储的 area_info_t 结构进行赋值。*/ai = (area_info_t *) ib->ptr.buffer;ai->next = 0;ai->end = lb;return ib;
}

经过 process_area() 初始化以后，内存池中的数据结构：
在这里插入图片描述

初始化时一共创建了3个内存块:

ib。系统内存块不会释放，用来存储内存池控制头部 area_head 指向的 area_info_t 存储空间。
b。用户可用的内存块，后面用户可分配得到的内存都来自于这一块内存。
lb。系统内存块不会释放，表示当前内存池的结束，area_info_t->end 会指向这里。

每个内存块的头部都是 bhdr_t 控制结构，实际数据从 bhdr_t->ptr.buffer[] 开始存储。

2.3 free

在 process_area() 初始化以后，就会调用 free_ex() 函数将内存块 b 释放给内存池。我们继续分析具体过程：

void free_ex(void *ptr, void *mem_pool)
{tlsf_t *tlsf = (tlsf_t *) mem_pool;bhdr_t *b, *tmp_b;int fl = 0, sl = 0;if (!ptr) {   return;}/* (5.1) 从内存块的数据地址，计算出内存块的控制结构地址 */b = (bhdr_t *) ((char *) ptr - BHDR_OVERHEAD);/* (5.2) 将当前内存块的状态改为 free */b->size |= FREE_BLOCK; TLSF_REMOVE_SIZE(tlsf, b);  /*  #if TLSF_STATISTIC */b->ptr.free_ptr.prev = NULL;b->ptr.free_ptr.next = NULL;/* (5.3) 尝试和后面的相邻物理块进行合并，如果它也是 free 的话 */tmp_b = GET_NEXT_BLOCK(b->ptr.buffer, b->size & BLOCK_SIZE);    /* 得到b后面的相邻物理块指针*/if (tmp_b->size & FREE_BLOCK) {                                 /* b后面块是free的？ */MAPPING_INSERT(tmp_b->size & BLOCK_SIZE, &fl, &sl);         /* 根据tmp_b大小求出一级与二级索引值 */EXTRACT_BLOCK(tmp_b, tlsf, fl, sl);                         /* 摘出可合并块 */b->size += (tmp_b->size & BLOCK_SIZE) + BHDR_OVERHEAD;      /* 把b（ptr）后面的内存块合并到b内存块中，size更新*/}/* (5.4) 尝试和前面的相邻物理块进行合并，如果它也是 free 的话 */if (b->size & PREV_FREE) {                                      /* b前一块free？ */tmp_b = b->prev_hdr;                                        /* 得到b前一物理块指针 */MAPPING_INSERT(tmp_b->size & BLOCK_SIZE, &fl, &sl);         /* 根据tmp_b大小求出一级与二级索引值 */EXTRACT_BLOCK(tmp_b, tlsf, fl, sl);                         /* 摘出可合并块 */tmp_b->size += (b->size & BLOCK_SIZE) + BHDR_OVERHEAD;      /* 更新新块的size */b = tmp_b;                                                  /* 更新b指针的值，即b指向合并后的内存块地址 */}/* (5.5) 将合并后的空闲块插入 free list 链表 */MAPPING_INSERT(b->size & BLOCK_SIZE, &fl, &sl);                 /*  */INSERT_BLOCK(b, tlsf, fl, sl);                                  /* 把释放的内存块插入相应链表的表头 *//* (5.6) 更新相邻物理后块对当前块的引用指针和free状态 */tmp_b = GET_NEXT_BLOCK(b->ptr.buffer, b->size & BLOCK_SIZE);tmp_b->size |= PREV_FREE;                                       /* 更新后一块的信息，以表示释放的内存块空闲的*/tmp_b->prev_hdr = b;                                            /* 更新后一块内存块的物理块prev_hdr*/ 
}#define INSERT_BLOCK(_b, _tlsf, _fl, _sl) do { \_b -> ptr.free_ptr.prev = NULL;  \                              /* 插入表头，则前项指针为空 */_b -> ptr.free_ptr.next = _tlsf -> matrix [_fl][_sl]; \if (_tlsf -> matrix [_fl][_sl]) \                               /* 若原链表非空，原表头的前项指针指向_b内存块，以形成双向链表 */_tlsf -> matrix [_fl][_sl] -> ptr.free_ptr.prev = _b; \_tlsf -> matrix [_fl][_sl] = _b; \set_bit (_sl, &_tlsf -> sl_bitmap [_fl]);\                      /* 更新位图标志位 */ set_bit (_fl, &_tlsf -> fl_bitmap); \
} while(0)

经过 free_ex() 以后内存池的状态：

在这里插入图片描述

2.4 malloc

malloc 流程就非常清晰和简单了，主要流程就在二级空闲链表 bhdr_t *matrix[REAL_FLI][MAX_SLI] 中查找合适大小的空闲内存块并分配。

其中一个注意的点就是如果分配得到的是大块，还有一个切割的过程：

void *malloc_ex(size_t size, void *mem_pool)
{tlsf_t *tlsf = (tlsf_t *) mem_pool;bhdr_t *b, *b2, *next_b;int fl, sl;size_t tmp_size;/* (1) 分配的最小值不能小于MIN_BLOCK_SIZE，并且向上对齐 */size = (size < MIN_BLOCK_SIZE) ? MIN_BLOCK_SIZE : ROUNDUP_SIZE(size);/* Rounding up the requested size and calculating fl and sl *//* (2) 查找 size 对应的 一级索引fl 和 二级索引sl */MAPPING_SEARCH(&size, &fl, &sl); /* Searching a free block, recall that this function changes the values of fl and sl,so they are not longer valid when the function fails *//* (3) 根据fl与sl的值，得到适合的空闲链表的表头*/b = FIND_SUITABLE_BLOCK(tlsf, &fl, &sl);  /* 以下部分是用于当前内存池中，没有所需内存块时，从内存中得到新的内存区（使用sbrk or mmap函数）*/
#if USE_MMAP || USE_SBRK......
#endif/* (3.1) 如果b空闲链表表头为NULL，表示分配内存失败！*/if (!b)    return NULL;            /* Not found *//* (3.2) 从对应 free list 中摘出一个内存块 */EXTRACT_BLOCK_HDR(b, tlsf, fl, sl);  /*-- found: *//* (3.3) 得到后面物理相邻内存块指针 */next_b = GET_NEXT_BLOCK(b->ptr.buffer, b->size & BLOCK_SIZE);/* Should the block be split? *//* (4.1) 如果分配得到的是大块内存，把内存分割，把多余内存归还给内存池 */tmp_size = (b->size & BLOCK_SIZE) - size;if (tmp_size >= sizeof(bhdr_t)) {                   /* 需要分割 */tmp_size -= BHDR_OVERHEAD;    b2 = GET_NEXT_BLOCK(b->ptr.buffer, size);       /* 切割剩余的空闲内存块 */b2->size = tmp_size | FREE_BLOCK | PREV_USED;   /* 为分割下来的内存块的size赋值*/next_b->prev_hdr = b2;                          /* next_b内存块链接相邻的前一个物理内存块*/MAPPING_INSERT(tmp_size, &fl, &sl);             /* 查找剩余内存块的空闲链表的一级与二级索引值*/INSERT_BLOCK(b2, tlsf, fl, sl);                 /*  插入内存块，且总是查入表头*//*add by vector,right?*/ b2->prev_hdr = b;                               /* 更新b2块的前一块的内存地址，*//*  size后两位更新，只把0bit改为USED_BLOCK*/b->size = size | (b->size & PREV_STATE);        /* 参数size为所需内存大小，更新b块的状态*/ /* (4.2) 所得内存块不需要分割，只需更新后面物理相邻内存块的标志 */} else {                                    next_b->size &= (~PREV_FREE);   b->size &= (~FREE_BLOCK);       /* Now it's used */}/* 更新统计值 */TLSF_ADD_SIZE(tlsf, b);return (void *) b->ptr.buffer;
}