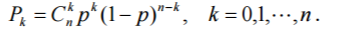排队论模型（四）：M / M / s 混合制排队模型

article/2025/10/17 3:42:20

排队论模型（一）：基本概念、输入过程与服务时间的常用概率分布

排队论模型（二）：生灭过程、 M / M /s 等待制排队模型、多服务台模型

排队论模型（三）：M / M / s/ s 损失制排队模型

排队论模型（四）：M / M / s 混合制排队模型

排队论模型（五）：有限源排队模型、服务率或到达率依赖状态的排队模型

排队论模型（六）：非生灭过程排队模型、爱尔朗（Erlang）排队模型

排队论模型（七）：排队系统的优化

排队论模型（八）：Matlab 生成随机数、排队模型的计算机模拟

1 单服务台混合制模型

2 多服务台混合制模型

1 单服务台混合制模型

单服务台混合制模型 M / M /1/ K 是指：顾客的相继到达时间服从参数为λ 的负指数分布，服务台个数为1，服务时间V 服从参数为 μ 的负指数分布，系统的空间为 K ，当 K 个位置已被顾客占用时，新到的顾客自动离去，当系统中有空位置时，新到的顾客进入系统排队等待。

由于排队系统的容量有限，只有 K −1个排队位置，因此，当系统空间被占满时，再来的顾客将不能进入系统排队，也就是说不能保证所有到达的顾客都能进入系统等待服务。假设顾客的到达率（单位时间内来到系统的顾客的平均数）为 λ ，则当系统处于状态 K 时，顾客不能进入系统，即顾客可进入系统的概率是 $\large 1- p_{K}$ 。因此，单位时间内实际可进入系统的顾客的平均数为：

例 5 某修理站只有一个修理工，且站内最多只能停放 4 台待修的机器。设待修机器按 Poisson 流到达修理站，平均每分钟到达 1 台；修理时间服从负指数分布，平均每 1.25 分钟可修理 1 台，试求该系统的有关指标。

解该系统可看成是一个 M / M /1/ 4 排队系统，其中

编写 LINGO 程序如下：

model:
sets:
state/1..4/:p;
endsets
lamda=1;mu=1/1.25;rho=lamda/mu;k=4;
lamda*p0=mu*p(1);
(lamda+mu)*p(1)=lamda*p0+mu*p(2);
@for(state(i)|i #gt#1 #and# i #lt#
k:(lamda+mu)*p(i)=lamda*p(i-1)+mu*p(i+1));
lamda*p(k-1)=mu*p(k);
p0+@sum(state:p)=1;
P_lost=p(k);lamda_e=lamda*(1-P_lost);
L_s=@sum(state(i)|i #le#k:i*p(i));
L_q=L_s-(1-p0);
W_s=L_s/lamda_e;
W_q=W_s-1/mu;
end

2 多服务台混合制模型

多服务台混合制模型 M / M / s/ K 是指顾客的相继到达时间服从参数为λ 的负指数分布，服务台个数为 s ，每个服务台服务时间相互独立，且服从参数为 μ 的负指数分布，系统的空间为 K 。

由式（4），式（5）和式（6），并注意到在本模型中

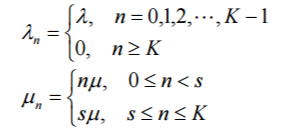
于是

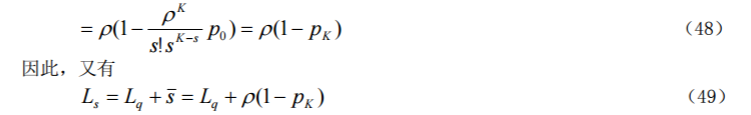
例 6 某汽车加油站设有两个加油机，汽车按 Poisson 流到达，平均每分钟到达 2 辆；汽车加油时间服从负指数分布，平均加油时间为 2 分钟。又知加油站上最多只能停放 3 辆等待加油的汽车，汽车到达时，若已满员，则必须开到别的加油站去，试对该系统进行分析。

解可将该系统看作一个 M / M / 2 / 5 排队系统，其中

编写 LINGO 程序如下：

model:
sets:
state/1..5/:p;
endsets
lamda=2;mu=0.5;rho=lamda/mu;s=2;k=5;
lamda*p0=mu*p(1);
(lamda+mu)*p(1)=lamda*p0+2*mu*p(2);
@for(state(i)|i #gt#1 #and# i #lt# s:
(lamda+i*mu)*p(i)=lamda*p(i-1)+(i+1)*mu*p(i+1)); 
@for(state(i)|i #ge# s #and# i #lt# k:
(lamda+s*mu)*p(i)=lamda*p(i-1)+s*mu*p(i+1));
lamda*p(k-1)=s*mu*p(k);
p0+@sum(state:p)=1;
P_lost=p(k);lamda_e=lamda*(1-P_lost);
L_s=@sum(state(i):i*p(i));
L_q=L_s-lamda_e/mu;
W_s=L_s/lamda_e;
W_q=W_s-1/mu;
end

在对上述多服务台混合制排队模型 M / M / s/ K 的讨论中，当 s = K 时，即为多服务台损失制系统。对损失制系统，有