Preliminary Questions
1.What does affect the performance of
——a computer system?
——a computer network?
——an Internet service?
2 How do we measure the performance of
——a computer system?
——a computer network?
——an Internet service?
想象如果我们只有一个作业,性能将仅仅会取决于系统硬件以及执行作业的程序。但是如果我们的作业多于一个呢?
Queueing Theory
排队论可以运用在任何队列中,是一门研究如何产生队列以及如何让队列消失的学科。
Queue Examples
disk,memory,CPU-有时候更好的设备并不会导致更好的更佳的性能
register at the supermarket
rates in a network
lock queue in a database -在队列中等待进行数据库的修改
virtual network functions in a service chain
access to bandwidth in cellular net
purpose
1 预测系统性能
2 设计来提高系统性能
3 测量系统性能
4 优化系统性能
Stochastic Modeling and analysis
排队论是基于更广泛的数学领域:随机建模和分析。系统中最重要的部分通过随机变量来表示,如:interarrival time(1/λ),service time(1/μ),waiting time()
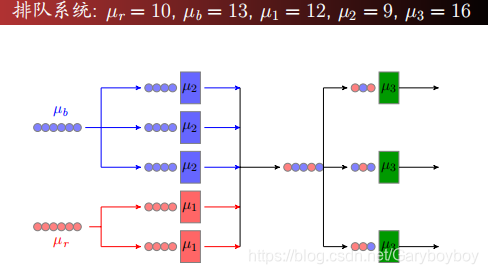
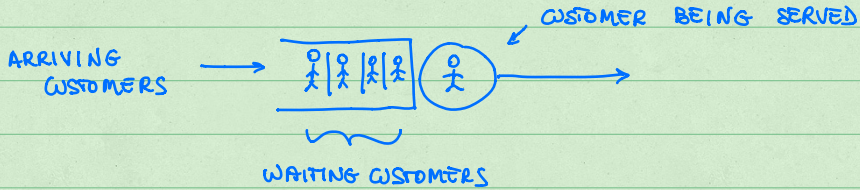
A motiving example

上图为一个系统,包括了:单一CPU,一个无限(或者有限)的queue,并且为FCFS
平均到达率average arrival rate:λ=3 jobs/sec
平均服务率average service rate:μ=5 jobs/sec
当λ<μ时不会overload,但是由于随机性,依然可能会产生队列
Q1:如果我们知道了=
(到达率加倍)。你需要买一个更快的CPU来保证有同样的响应时间、那么你应该如何增加CPU的速度呢?
A1:Less than double
到目前为止我们还没有工具能准确的计算出来,但是我们可以预想如果同时加倍CPU速度和到达率,那么响应时间会减半。原因:假设在A,B两个世界里的科学家进行同样的工作。A世界的科学家使用更慢的时钟,B世界的科学家使用更快的时钟,A世界的时钟过1s,B世界的时钟则过2s。两个科学家使用相同的标准并且是本地测量λ(即A,B的λ和μ对于他们来说从数值上都是一样的)。所以A到了一个作业的时间,B到达了两倍多的作业。同样,A处理完一个作业的时间,B处理完了两倍多的作业。但是响应时间却不相同而是减半了(因为同样标准下对于他们自身时钟来看,A,B的响应时间应该也是一样的,但是B中的时间比A中的快一倍)。
Q2:如果CPU采用了不同的服务原则呢?
A2:nothing changes 。同样,有时候硬件的提升也无法提升系统性能。
Single server network
a single server network is defined by:
- service order:FCFS,SJF,SRPT
- average arrival rate λ
- mean interarrival time 1/λ
- service requirement:S
- mean service time E[S]=1/μ
- average service rate μ
- number of jobs in the system N
- number of jobs in queue
- loss or drop rate/probability
Observations
Q:如果λ>μ会发生什么?
A:无穷大,t
无穷大
(因为这里预期的离开数量会小于实际的,因为会有时间队列为空)
因此λ<μ 是Stability Condition
E[N(t)]:jobs in system at time t
E[A(t)]:arriving upto t
E[D(t)]:departure upto t
Through Put and Utilization
吞吐量throught put :rate of completions seen at device i
注意rate of completions 不等于 service rate,并且同一个系统中每个设备的吞吐可以不一样
利用率utilization:fraction time the service is busy
:观察时间
B:在观察时间内设备忙碌的时间