一、tlsf算法介绍

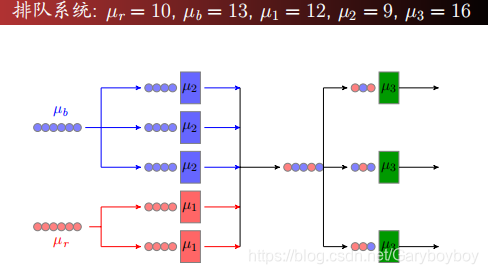
tlsf（全称Two-Level Segregated Fit，内存两级分割策略算法），第一级（first level，简称fl）将内存大小按2的幂次方划分一个粗粒度的范围，如一个72字节的空闲内存的fl是6（72介于2⁶和2⁷之间），第二级（second level，简称sl）在第一级的基础上做线性化的细粒度划分，分为多少等份由可配置的SLI参数确定，在32bit的系统中，最优的SLI是4或者5，若为4，则等分为2⁴=16份，每一份分割叫做Segregated list（分割链表），如下图中的[104…111]，链表上挂着的是大小范围为104…111的free blocks，数字104…111代表的是内存的大小，而非内存地址，tlsf算法将内存分成不同大小的块，如下图的[104…111]这个分割链表管理了两个内存块，一个大小109字节，一个大小104字节。前面介绍了tlsf算法会对内存按照大小做两级分割，接着讨论怎么根据内存大小查找free block，tlsf算法根据需要的内存大小根据前面的两级分割算法计算出fl和sl，采用good fit策略，分割链表中的free block都必须大于需要的内存大小，如需要一个72字节的内存，假设SLI=2（简单起见，做4等分），则fl=6，sl=0，加入选择sl=0这个分割链表，则由于67小于72，不满足分割列表中所有free block大于需要的内存的条件，所以需要取sl=1，如果sl=1这个分割链表不为空则返回这个链表中的第一个free block给到应用程序。
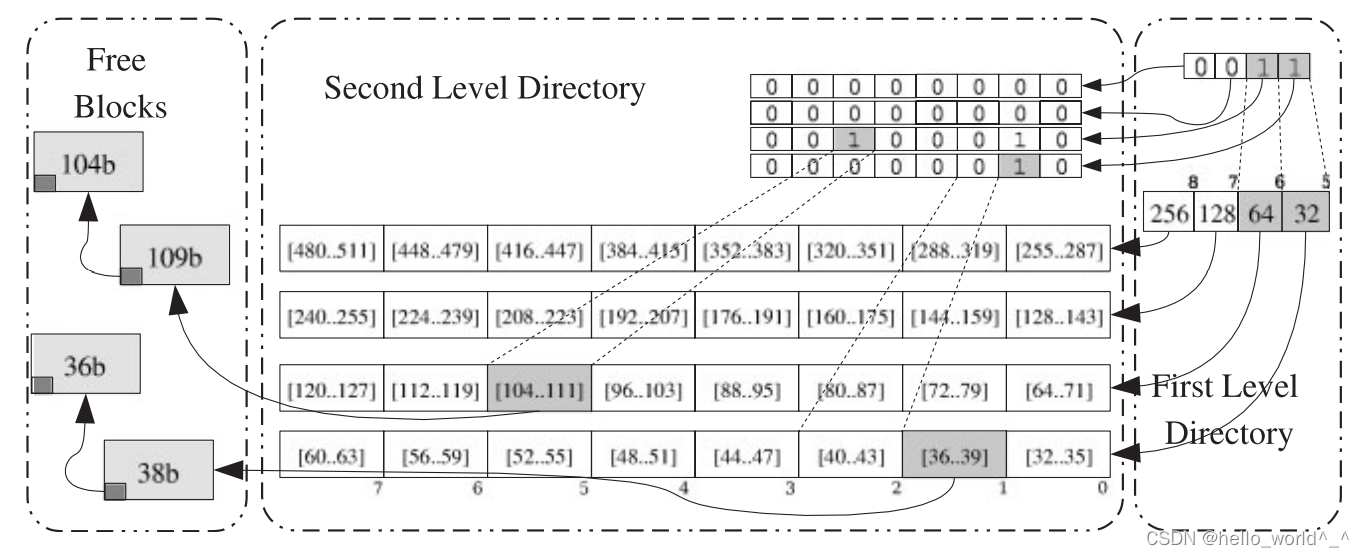
在这里插入图片描述

二、tlsf代码分析

tlsf在tlsf_malloc中先调用block_locate_free获取free block，再调用block_prepare_used获取free block的内存地址返回给应用程序。在这个过程中，与good fit相关的是两个函数mapping_search和search_suitable_block。

2.1 mapping_search

/* This version rounds up to the next block size (for allocations) */
static void mapping_search(size_t size, int* fli, int* sli)
{if (size >= SMALL_BLOCK_SIZE){const size_t round = (1 << (tlsf_fls_sizet(size) - SL_INDEX_COUNT_LOG2)) - 1;size += round;}mapping_insert(size, fli, sli);
}
//在mapping_search调用mapping_insert
/*
** TLSF utility functions. In most cases, these are direct translations of
** the documentation found in the white paper.
*/static void mapping_insert(size_t size, int* fli, int* sli)
{int fl, sl;if (size < SMALL_BLOCK_SIZE){/* Store small blocks in first list. */fl = 0;sl = tlsf_cast(int, size) / (SMALL_BLOCK_SIZE / SL_INDEX_COUNT);}else{fl = tlsf_fls_sizet(size);//计算first level indexsl = tlsf_cast(int, size >> (fl - SL_INDEX_COUNT_LOG2)) ^ (1 << SL_INDEX_COUNT_LOG2);//计算second level indexfl -= (FL_INDEX_SHIFT - 1);}*fli = fl;*sli = sl;
}

mapping_search先对size做一个四舍五入，再根据size计算fl和sl的索引，这个fl和sl索引作为下一步的search_suitable_block的起点。

2.2 search_suitable_block

static block_header_t* search_suitable_block(control_t* control, int* fli, int* sli)
{int fl = *fli;int sl = *sli;/*首先，在与给定的fl/sl索引相关的分割链表中搜索一个free block。*/unsigned int sl_map = control->sl_bitmap[fl] & (~0U << sl);if (!sl_map){/* 没有free block存在，搜索下一个first level */const unsigned int fl_map = control->fl_bitmap & (~0U << (fl + 1));if (!fl_map){/* 没有可用的free block，内存已经用完。*/return 0;}fl = tlsf_ffs(fl_map);*fli = fl;sl_map = control->sl_bitmap[fl];}tlsf_assert(sl_map && "internal error - second level bitmap is null");sl = tlsf_ffs(sl_map);*sli = sl;/* 返回分割链表的第一个free block */return control->blocks[fl][sl];
}