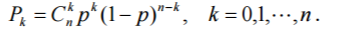排队系统

顾客输入过程

• 顾客源（总体）：有限/无限
• 顾客到达方式：逐个/逐批（主要是逐个）
• 顾客到达间隔：随机型/确定型
• 顾客到达：相互独立/相互关联
• 输入过程：平稳/非平稳

排队结构与排队规则

• 顾客排队方式：等待制/即时制
• 排队系统容量：有限制/无限制
• 排队队列数目：单列/双列
• 中途是否退出：允许/禁止
• 是否允许列间转移：允许/禁止

服务机构与服务规则

• 服务台数量：单个/多数
• 服务台排列形式：并联/串联/混合
• 服务台服务方式：逐个/逐批
• 服务时间分布：随机型/确定型
• 服务时间分布是否平稳：平稳/非平稳

服务台给顾客的服务顺序

• 先来先服务
• 后到先服务
• 随机服务
• 优先服务

达到间隔与服务时间的典型分布

• 泊松分布 $ M$
• 负指数分布 $ M$
• k阶埃尔朗分布 $E_K$
• 确定型分布 $ D$
• 一般服务时间分布 $ G$

排队模型

系统运行状态参数

• 系统状态$N(t)$

  排队系统在t时刻的全部顾客数$N$ ,包括“排队顾客数”和“正在被服务顾客数”

• 系统状态概率

  a.瞬间概率$P_n（t）$ ：系统t时刻的系统状态$N(t)=n$ 的概率

  b.稳态概率$P_n$ : $P_n= \lim_{n\rightarrow+\infty} P_n(t) $ .排队系统运行了一定长的时间后系统状态的概率不再随时间t变化

系统运行指标参数(评价参数)

• 队长$L_s$

  系统中的顾客数（n）期望值记为$L_s$ （排队中以及服务中）

• 排队长$L_q$

  系统中排队等待服务的顾客数，期望值为$L_q$

• 逗留时间$W_s$

  一个顾客在系统中停留的总时间，期望为$W_s$

• 等待时间$W_q$

  一个顾客在系统中的排队等待时间，期望为$W_q$

  于是有$W_s$ =$W_q$ +$W_{服务}$

• 忙期

  从顾客到达空闲服务机构起到服务机构再次空闲的时间长度

• 忙期服务量

  一个忙期内系统平均完成服务的顾客数

• 损失率

  顾客到达排队系统，未接受服务而离开的概率

• 服务强度：$\rho =\lambda /\mu s$

  $\lambda$指单位时间到达排队系统的人数， s指服务台的数量，$\mu$ 指单位时间能够服务的顾客数

泊松流与泊松分布

一般我们认为顾客达到和顾客服务时间的概率是按泊松流的概率分布来的

泊松流满足三个条件：

1.每一时段到达系统的顾客数相互独立，即无后效性

2.在充分小的时间间隔内$ [t,t+\Delta t]$，到达一个顾客的概率与时间t无关，仅与时间间隔成正比，有$P_{(t,t+\Delta t)}=\lambda\Delta t+\omicron(\Delta t)$ ,即平稳性

3.对于充分小的时间间隔$ [t,t+\Delta t]$ ，两个及以上的顾客到达的概率可忽略不计，即普通性

泊松流到达的间隔服从负指数分布

• 顾客到达间隔T的概率密度为：
  $$f_T\text{（}t\text{）}=\{\begin{array}{l}\lambda e\stackrel{-\lambda t}{},t⩾0\\ 0,t<0\end{array}$$

• 顾客到达间隔T的分布函数为：
  $$F_T\text{（}t\text{）}=\{\begin{array}{l}1-\lambda e\stackrel{-\lambda t}{},t⩾0\\ 0,t<0\end{array}$$
  由概率论的知识我们可以知道
  $$E\left[T\right]=1/\lambda ;Var\left[T\right]=1/{\lambda }^2;\sigma \left[T\right]=1/\lambda$$

顾客服务时间服从负指数分布

对一个顾客的服务时间$T_s$,等价于相邻两个顾客离开排队系统的时间间隔

• 顾客到达间隔$T_s$ 的概率密度为：
  $$f_{T_s}\text{（}t\text{）}=\{\begin{array}{l}\lambda e\stackrel{-\lambda t}{},t⩾0\\ 0,t<0\end{array}$$

• 顾客到达间隔$T_s$的分布函数为：
  $$F_{T_s}\text{（}t\text{）}=\{\begin{array}{l}1-\lambda e\stackrel{-\lambda t}{},t⩾0\\ 0,t<0\end{array}$$
  由概率论的知识我们可以知道
  $$E\left[T_s\right]=1/\lambda ;Var\left[T_s\right]=1/{\lambda }^2;\sigma \left[T_s\right]=1/\lambda$$

  ---

单服务台负指数分布M/M/1排队系统

模型满足的条件

1.输入过程：顾客源是无限随机的，逐个到来，服从泊松分布

2.排队规则：单队，无队长限制，先到先服务

3.服务机构：单服务台，服务时间的长短随机，服从泊松分布

该模型的公式

$$\begin{gathered} P_0=1-\rho P_n={\rho }^n\left(1-\rho \right) \\ {L}_s=\frac{\lambda }{\mu -\lambda }=\frac{\rho }{1-\rho }{L}_q=\frac{{\lambda }^2}{\mu \left(\mu -\lambda \right)}=\frac{{\rho }^2}{1-\rho }=L_s\rho \\ {W}_s=\frac{1}{\mu -\lambda }{W}_q=\frac{\lambda }{\mu \left(\mu -\lambda \right)}=W_s\rho \\ P\left(N>k\right)={\rho }^{k+1}N\text{表示系统中的顾客数} \end{gathered}$$

模型举例

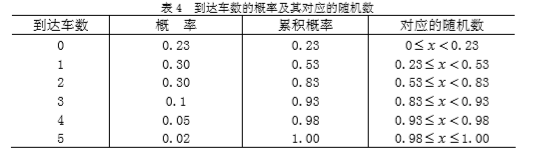
某医院急诊室同时只能诊治一个病人，诊治时间服从指数分布，每个病人平均需要15分钟。病人按泊松分布到达，平均每小时到达3人。试对此排队队系统进行分析

1.确定参数

$$\lambda =3,s=1,\mu =60/15=4，\rho =\frac{\lambda }{s\mu }=0.75$$

2.计算稳态概率

急诊室空闲，即病人能立即就医的概率
$$P_0=1-\rho =0.25$$
急诊室繁忙，即病人需等待就医的概率为服务强度，即0.75

3.计算系统主要工作指标

急诊室内外的病人平均数：

$L_s=\frac{\lambda }{\mu -\lambda }=3$

急诊室外排队等待的病人平均数：

$L_q=L_s\rho =2.25
$

病人在急诊室内外平均逗留时间：

$
W_s=\frac{1}{\mu -\lambda}=60\min
$

病人平均等候时间：

$
W_q=W_s\rho =45\min$

M/M/S排队系统

此模型与M/M/1模型不同之处在于有S个服务台，各服务台的工作相互独立，服务率相等，如果顾客到达时，S个服务台都忙着，则排成一队等待，先到先服务的单队模型(该模型非常公平)

整个系统的平均服务率为sμ，ρ＝λ/sμ，（ρ<1）为该系统的服务强度

1.状态概率

$$\begin{gathered} P_0={\left[\sum _{k=0}^{s-1}\frac{1}{k!}\left(\frac{\lambda }{\mu }\right)+\frac{1}{s!}\frac{1}{1-\rho }{\left(\frac{\lambda }{\mu }\right)}^s\right]}^{-1} \\ {P}_n=\{\begin{array}{l}\frac{1}{n!}{\left(\frac{\lambda }{\mu }\right)}^n{P}_{0}0<n⩽S\\ \frac{1}{S!S^{n-S}}{\left(\frac{\lambda }{\mu }\right)}^n{P}_{0}n⩾S\end{array} \end{gathered}$$

2.主要评价指标

$$\begin{gathered} {L}_q=\frac{{\left(S\rho \right)}^S\rho }{S\text{！（}1-\rho {\text{）}}^2}{P}_0{L}_s=L_q+S\rho \\ {W}_q=\frac{L_q}{\lambda }{W}_s=\frac{L}{\lambda }=W_q+\frac{1}{\mu } \end{gathered}$$

3.系统状态$ N\geqslant k$ 的概率

$P\left( N\geqslant k \right) =\sum_{n=k}^{\infty}{P_n}=\frac{\rho ^k}{k\text{！（}1-\rho \text{）}}P_0,, $

4.模型举例

某医院急诊室同时能同时诊治两个病人，并且平均服务率相同，诊治时间服从指数分布，每个病人平均需要15分钟。病人按泊松分布到达，平均每小时到达3人。试对此排队队系统进行分析

1.确定参数

$$\lambda =3,s=2,\mu =60/15=4，\rho =\frac{\lambda }{s\mu }=0.375$$

2.计算稳态概率

即病人能立即就医的概率
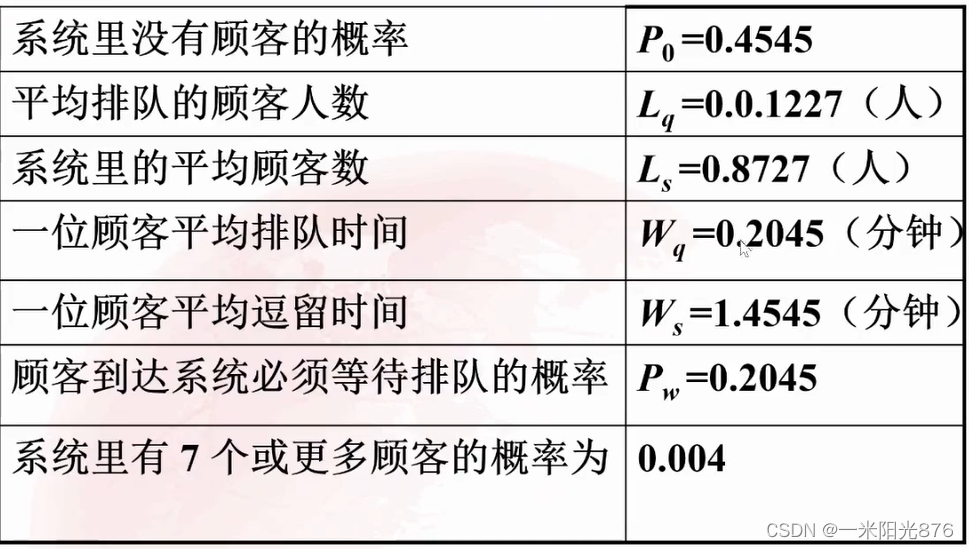
$$P_0={\left[\sum _{k=0}^{s-1}\frac{1}{k!}\left(\frac{\lambda }{\mu }\right)+\frac{1}{s!}\frac{1}{1-\rho }{\left(\frac{\lambda }{\mu }\right)}^s\right]}^{-1}=0.45$$

3.计算系统主要工作指标（评价模型好坏最重要的几个指标）

急诊室外排队等待的病人平均数：

$L_q=\frac{{\left(S\rho \right)}^S\rho }{S\text{！（}1-\rho {\text{）}}^2}{P}_0=0.12$

急诊室内外的病人平均数：

$ L_s=L_q+S\rho =0.87$

病人在急诊室内外平均逗留时间：

$
W_s=17.4\min
$

病人平均等候时间：

$
W_q=2.4\min$

病人必须等候的概率：

$P\left( N\geqslant 2 \right) =\sum_{n=2}^{\infty}{P_n}=\frac{\rho ^2}{2\text{！（}1-\rho \text{）}}P_0,, $=0.20

排队论代码部分

单服务台负指数分布M/M/1排队系统

clear 
clc 
%***************************************** 
%初始化顾客源 
%***************************************** 
%总仿真时间 
Total_time = 10; 
%队列最大长度(无穷) 
N = 10000000000; 
%到达率与服务率 
lambda = 10; 
mu = 6; 
%平均到达时间与平均服务时间 
arr_mean = 1/lambda; 
ser_mean = 1/mu; 
arr_num = round(Total_time*lambda*2); 
events = []; 
%按负指数分布产生各顾客达到时间间隔 
events(1,:) = exprnd(arr_mean,1,arr_num); 
%各顾客的到达时刻等于时间间隔的累积和 
events(1,:) = cumsum(events(1,:)); 
%按负指数分布产生各顾客服务时间 
events(2,:) = exprnd(ser_mean,1,arr_num); 
%计算仿真顾客个数，即到达时刻在仿真时间内的顾客数 
len_sim = sum(events(1,:)<= Total_time); 
%***************************************** 
%计算第 1个顾客的信息 
%***************************************** 
%第 1个顾客进入系统后直接接受服务，无需等待 
events(3,1) = 0; 
%其离开时刻等于其到达时刻与服务时间之和 
events(4,1) = events(1,1)+events(2,1); 
%其肯定被系统接纳，此时系统内共有 
%1个顾客，故标志位置1 
events(5,1) = 1; 
%其进入系统后，系统内已有成员序号为 1 
member = [1]; 
for i = 2:arr_num 
%如果第 i个顾客的到达时间超过了仿真时间，则跳出循环 if events(1,i)>Total_time break; else 
number = sum(events(4,member) > events(1,i)); 
%如果系统已满，则系统拒绝第 i个顾客，其标志位置 0 
if number >= N+1 
events(5,i) = 0; 
%如果系统为空，则第 i个顾客直接接受服务 
else 
if number == 0 
%其等待时间为 02009.1516%PROGRAMLANGUAGEPROGRAMLANGUAGE
events(3,i) = 0; 
%其离开时刻等于到达时刻与服务时间之和 
events(4,i) = events(1,i)+events(2,i); 
%其标志位置 1 
events(5,i) = 1; 
member = [member,i]; 
%如果系统有顾客正在接受服务，且系统等待队列未满，则 第 i个顾客进入系统 else len_mem = length(member); 
%其等待时间等于队列中前一个顾客的离开时刻减去其到 达时刻 
events(3,i)=events(4,member(len_mem))-events(1,i); 
%其离开时刻等于队列中前一个顾客的离开时刻加上其服 
%务时间 
events(4,i)=events(4,member(len_mem))+events(2,i); 
%标识位表示其进入系统后，系统内共有的顾客数 
events(5,i) = number+1; 
member = [member,i]; 
end 
end end 
end 
%仿真结束时，进入系统的总顾客数 
len_mem = length(member); 
%***************************************** 
%输出结果 
%***************************************** 
%绘制在仿真时间内，进入系统的所有顾客的到达时刻和离 
%开时刻曲线图（stairs：绘制二维阶梯图） 
stairs([0 events(1,member)],0:len_mem); 
hold on; 
stairs([0 events(4,member)],0:len_mem,'.-r'); 
legend('到达时间 ','离开时间 '); 
hold off; 
grid on; 
%绘制在仿真时间内，进入系统的所有顾客的停留时间和等 
%待时间曲线图（plot：绘制二维线性图） 
figure; 
plot(1:len_mem,events(3,member),'r-*',1: len_mem,events(2,member)+events(3,member),'k-'); 
legend('等待时间 ','停留时间 '); 
grid on;

M/M/S排队系统

%修改前三个数据
s=2;
mu=4;
lambda=3;
ro=lambda/mu;
ros=ro/s;
sum1=0;for i=0:(s-1)sum1=sum1+ro.^i/factorial(i);
endsum2=ro.^s/factorial(s)/(1-ros);p0=1/(sum1+sum2);
p=ro.^s.*p0/factorial(s)/(1-ros);
Lq=p.*ros/(1-ros);
L=Lq+ro;
W=L/lambda;
Wq=Lq/lambda;
fprintf('排队等待的平均人数为%5.2f人\n',Lq)
fprintf('系统内的平均人数为%5.2f人\n',L)
fprintf('平均逗留时间为%5.2f分钟\n',W*60)
fprintf('平均等待时间为%5.2f分种\n',Wq*60)

!](https://img-blog.csdnimg.cn/20210201192334667.jpg?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L211YmliYWl3aGFsZQ==,size_16,color_FFFFFF,t_70#pic_center)