1 微分方程

（1）概念：微分方程是含有函数及其导数的方程，如果方程组只含有一个自变量（通常是时间t），则称为常微分方程，否则称为偏微分方程。
（2）建立微分方程模型：在自然科学以及工程、经济、医学、体育、生物、社会等学科中的许多系统，有时很难找到该系统有关变量之间的直接关系–函数表达式，但是却很容易找到这些变量和它们的微小增量或变化率之间的关系式，这时往往采用微分关系式来描述该系统—即建立微分方程模型
（3）微分方程的解是函数，对应一个变化过程。常微分方程的解释随时间t变化的函数，比如一辆汽车在公路上飞驰，一个球从空中落下。
偏微分方程不但描述物体随时间变化发生位置的改变而且描述物体各部分之间位置的相对变化。如水的流动,烟雾的扩散,公路上车流的涌动等

2 微分方程解决的主要问题

（1）描述对象特征随时间（空间）的演变过程
（2）分析对象特征的变化规律
（3）预报对象特征的未来性态
（4）研究控制对象特征的手段

3 微分方程模型

包括两个部分：方程和定解条件
• 常微分方程的定解条件：对一个m阶常微分方程，需要积分m次才能将解函数求出，因此需要m个定解条件。
• 方程组的定解条件个数是每个方程定解条件个数之和。
• 定解问题分为初值问题和边值问题。
• 初值问题的定解条件在同一个点上，而边值问题的定解条件在不同点上。

4 微分方程解决问题的一般步骤

第一步

注意到实际问题中有与数学中“导数”有关的常用词，
“速度”、“速率”（运动学、化学反应中），
“边际的”（经济学中）；
“增长”（生物学、金融、经济等中），
衰变（放射性问题中）；
以及与“改变，、'变化”、“增加”、减少”等有关词语，都可能是微分方程的问题。

第二步

梳理出实际问题中所涉及的各种量，使用一致的物理单位。

第三步

梳理出与结果有关的并且有着函数关系（待求）的量作为要求的函数的自变量与因变量，而与变化率有关的量，即是待求函数的导数。

5 微分方程举例

例1
某人的食量是2500卡1天。其中1200卡用于基本的新陈代谢。在健身训练中，他每公斤体重所消耗的热量大约是16卡/天。设以脂肪形式贮存的热量100％有效，且1公斤脂肪含热量10000卡，分析这个人体重的变化。分析:
问题研究人体重量随时间的变化w（t)。条件给出的是热量单位时间的变化
2500一1200一16w(t)
转换成体重为
（2500-1200-16w(t)）/10000
因此得到变化关系
dw/dt = (2500-1200-16w)/10000
例2
将一只读数为25度的温度计放在室外，10分钟后度数为30度，又过了10分钟，读数变为33度，问室外温度是多少？
热传导分析：
查一下热传导，我们可以了解到：热的传导从温度高的地方向温度低的地方传导，单位时间传送的热量与温差T成正比，与两个热源的距离成反比。即$\Delta$Q = k$\Delta$ T/d
对于两个固定热源，距离d是常数，则$\Delta$Q=$k_1\Delta$ T
在这个问题中，室外温度可以看做是常数T0，大于室内温度，而热量正比于温差，从而变化规律为dT/dt = -k($T$-$T_0$)

6 经典的微分方程模型

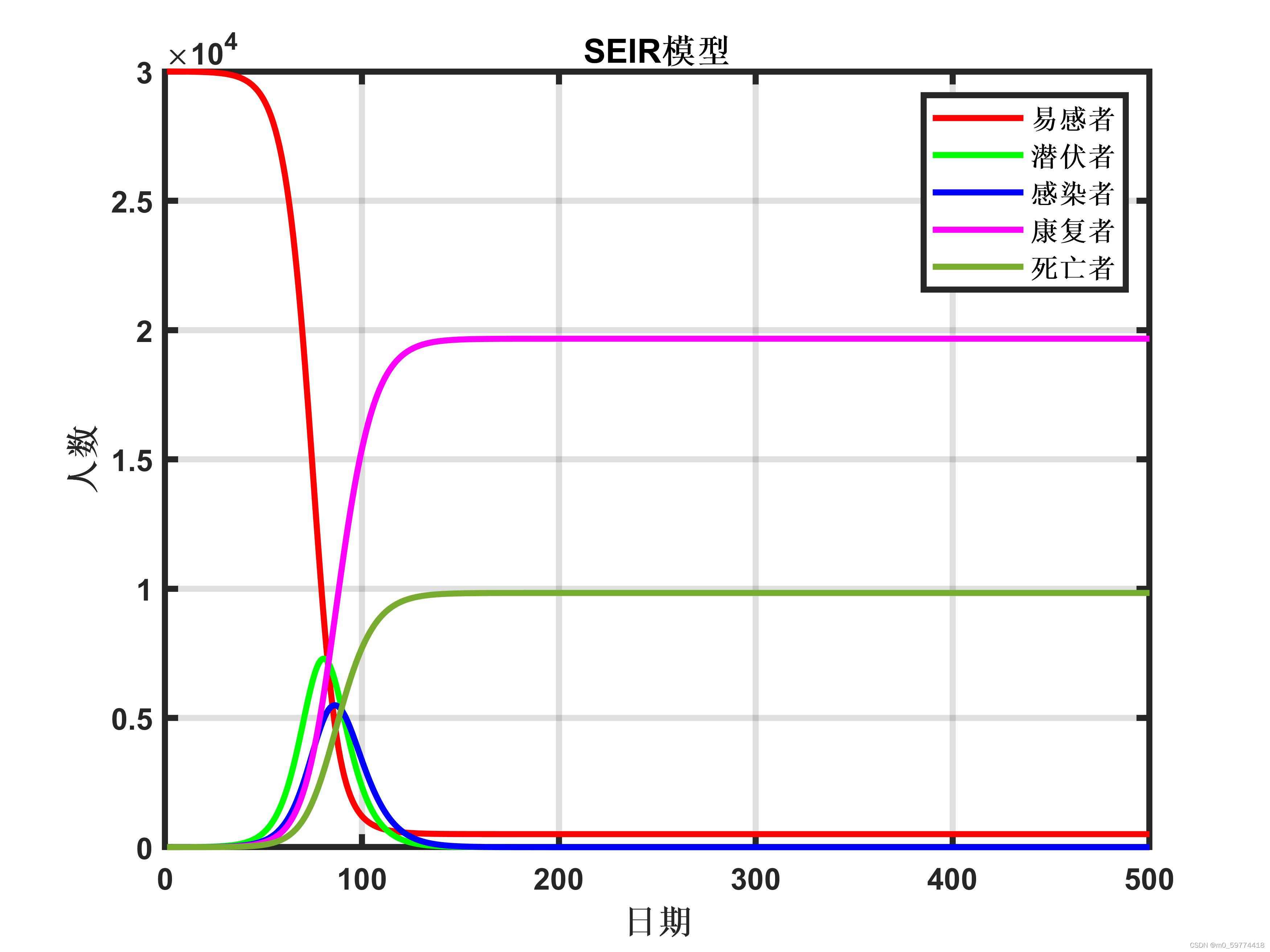
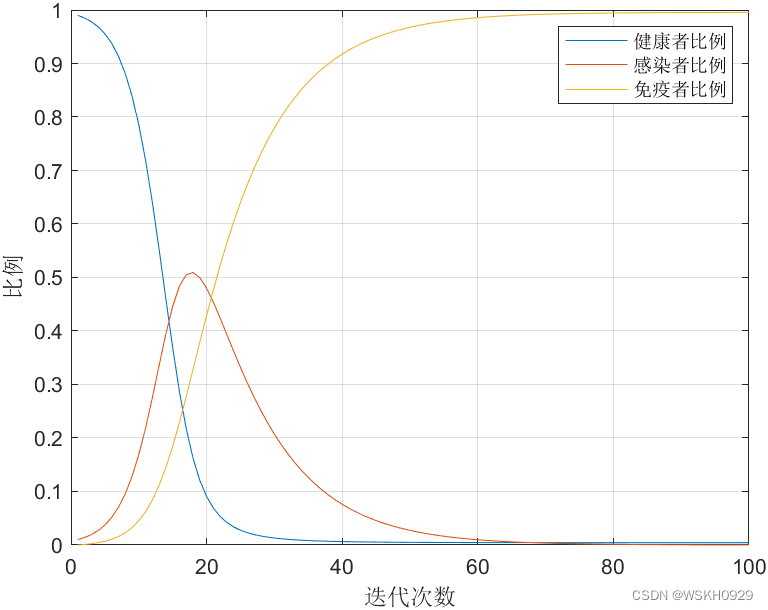
（1）传染病模型
（2）经济增长模型
（3）正规战与游击战
（4）药物在体内的分布与排除
（5）香烟过滤嘴的作用
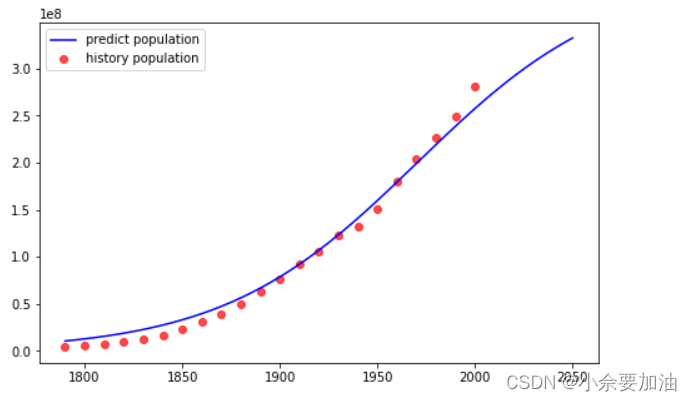
（6）人口预测和控制
（7）烟雾的扩散与消失
（8）万有引力定律的发现

7 课后习题

一只小船渡过宽为d的河流，目标是起点A正对着的另一岸B点，已知河流速度v与船在静水中的速度w之比为k。试建立小船航线的微分方程，求其解析解；
设d=100m，v=1m/s，w=2m/s,用数值解法求渡河所需的时间和任意时刻小船的位置及航行曲线。
解：
参考内容
（1）建立模型
如图所示，以B为原点，沿河岸向右为x轴正向，垂直河岸向下为y轴正向，建立坐标系。设在t时刻，船在x方向上的位移是x(t),在Y方向上的位移是y(t)。
• 在t时刻，船在x方向上的速度是$x‘(t)$ ，在y方向上的速度是$y‘(t)$，将船的速度v和水度v1在x，y轴方向上分解，可得：
$v_x=v_1-v_{2}sin\alpha$
$v_y=-v_{2}cos\alpha$

又因为船头始终指向B点，所以：

（2）数值解法
基本思路：先将微分方程和微分方程组整理成标准形式：
$\frac{dx}{dt}=f_x(x,y,t)$
$\frac{dx}{dt}=f_y(x,y,t)$
我们用一个很小的常数来代替，那么上式可以改写为：
$x(t+\Delta t)=f_x(x(t),y(t),t)\ast \Delta t+x(t)$
$y(t+\Delta t)=f_y(x(t),y(t),t)\ast \Delta t+x(t)$
我们只需要关心各个离散的x和y的值和位置，因此可将上式进一步整理得：
$y(n+1)=f_x(x(n),y(n),t_0+n\ast \Delta t)\ast \Delta t+x(n)$
$y(n+1)=f_y(x(n),y(n),t_0+n\ast \Delta t)\ast \Delta t+y(n)$
上式便是微分方程组数值解法的迭代公式，只要有初值x0,y0,t0和步长，通过迭代就可以得到微分方程组的离散近似解，从而可以绘制出微分方程组所描述的曲线。
利用数值方法，可以求得小船渡河的近似时间：$T=n\ast \Delta t$