注:本文是刘然对常微分方程模型的简介
什么是常微分方程模型
常用的回归分析聚焦于直接建立响应变量和协变量之间的关系,之后根据建立的模型进行分析和预测,比如常见的线性回归模型:。
而如果我们感兴趣的变量是随时间变化的,那么还有另外一种常用的建模方式:建立变量与变量对时间的导数之间的关系,这就是我们这里要介绍的常微分方程模型。容易理解,常微分方程模型是利用常微分方程来刻画变量之间的关系的模型。假设我们关心的变量为,常微分方程的数学形式写作: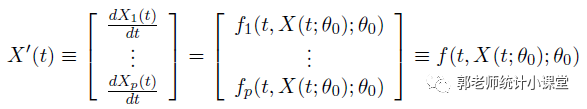
这里是线性或者非线性的函数,是未知的参数。在这种数学形式下,我们不是直接去建立变量之间的函数关系,而是通过常微分方程给出变量的导数和变量自身之间的函数关系。由于这里的一般大于1,这里给出的常微分方程一般是一个常微分方程组,构成了一个常微分方程系统。
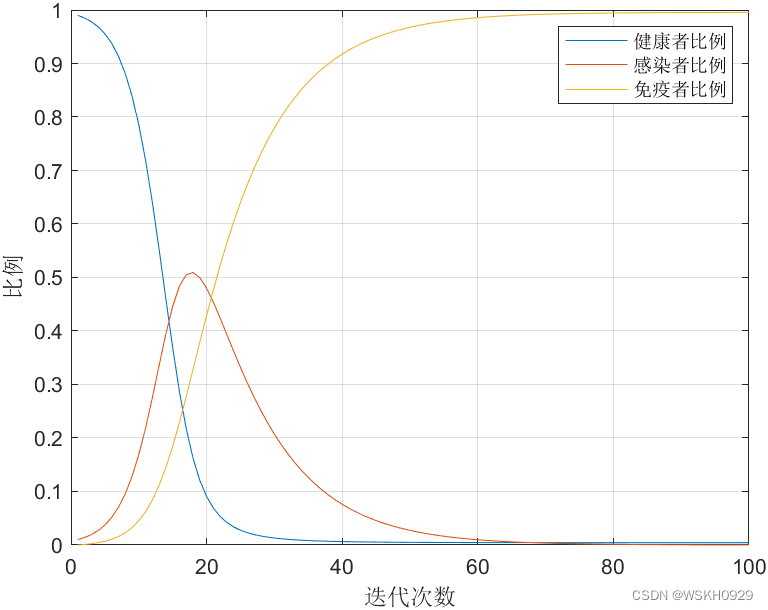
常微分方程模型在自然科学和社会科学中都得到了广泛的应用,比如神经科学中用来描述神经元发放的Hodgkin-Huxley Model,经济学中描述经济增长的Solow growth Model,以及传染病学中描述感染人数的SIR Model。