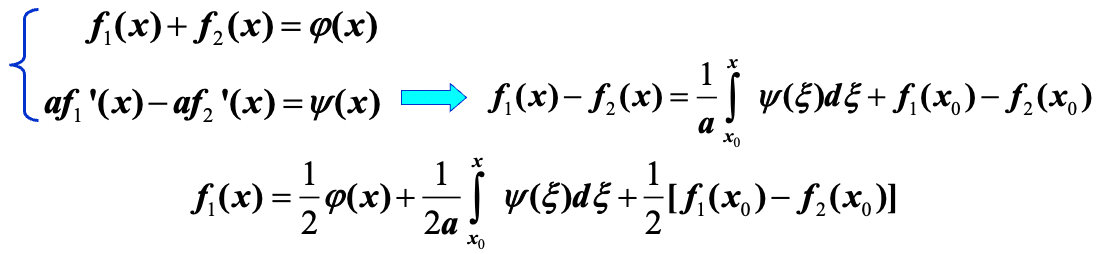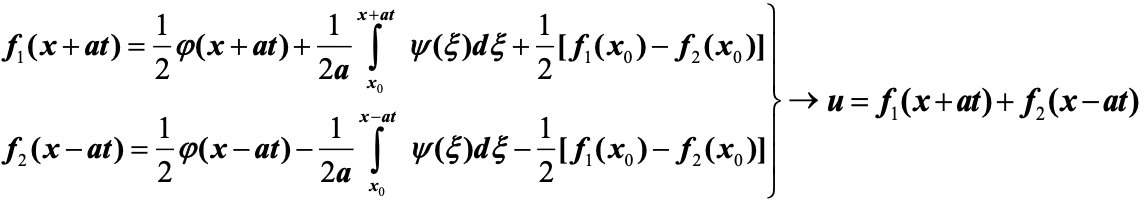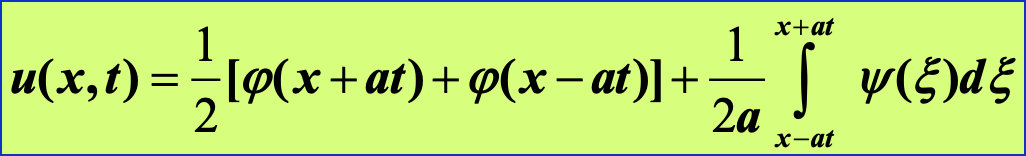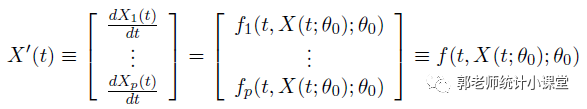1. 简介

微分方程：描述自然界中存在的物理现象和普遍规律。

常微分方程（ODE）
偏微分方程（PDE）

偏微分方程理论：

物理/工程问题————翻译（建模）/物理工程规律————》数学问题（PDE）
物理/工程问题————求解/数学理论————》数学结果
物理/工程问题————分析————》数学公式/物理意义

偏微分方程的基本概念：

定义：未知函数及其偏导数所满足的方程；F(x, u(x), Du, D²u,…, Dⁿu) = 0;
阶数：偏微分方程中偏导数的最高阶数，有n阶就为n。
线性偏微分方程：方程中的未知函数或其偏导数的项都是一次项。
齐次方程：每项都含有未知函数或未知函数（定义的u = u(x, y)）的偏导数。

导出微分方程的基本步骤：

明确研究的物理量
明确物理量遵守的物理规律
按物理规律写出微分方程（泛定方程）
微元法：划出一个微元，分析临近部分和ta的相互作用

微分方程解决的主要问题：

描述对象特征随时间变化的过程
分析对象特征的变化规律
预报对象特征的未来形态
研究控制对象特征的手段

常用的物理定律概述：

牛顿第二定律：F = ma；
胡克定律，在弹性限度内，弹性体的张应力和弹性体的形变量成正比：张应力 = 杨氏模量 * 相对伸长，
热传导的傅立叶定律：在dt时间内，通过面积元dS流入一个小体积元的热量dQ，与沿着面积元法线方向的温度梯度成正比，也与dS和dt成正比：（k是导热系数，由材料决定）
牛顿冷却定律：单位时间内从周围介质，传到边界上单位面积的热量，与表面和外界的温度差成正比：（这里u₁是外界媒质的温度，h为比例系数）
扩散定律（斐克定律）：单位时间流过某横截面的杂质量dm与该横截面积S和浓度梯度成正比：（式中D为扩散系数，负号是指杂质浓度在减少）

2. 栗子——香烟过滤嘴的作用

问题：

过滤嘴的作用和ta的材料与长度有什么关系；
人体吸入的毒品量和哪些因素有关，因素的影响程度怎么样

模型分析：

分析吸烟时毒物进入人体的模型，建立吸烟过程模型；
假设一个机器人持续吸烟，并且环境不变

模型假设（假设的变量都在这儿哦）：

烟草长 l₁，过滤嘴长 l₂，总长度 l = l₁ + l₂，假设毒品均匀分布；
毒物进入空气和沿香烟穿行的数量比：a’ : a, a’ + a = 1；
未点燃烟草和过滤嘴的吸收率（过滤程度）分别为b和ß；
烟雾沿着香烟的穿行速度为常速v，香烟的燃烧速度为u，v >> u；
Q为毒物进入人体的总量
q(x, t)为毒物的流量，w(x, t)为毒物密度

模型建立：

建立毒物进入身体的总量：Q = ƒ₀^T q(l, t)dt, T = l₁ / u;
求q(x, 0) = q(x)——流量守恒
q(x) - q(x + ∆x) = bq(x)∆∂, 0 ≤ x ≤ l₁;

q(x) - q(x + ∆x) = ßq(x)∆∂, l₁ ≤ x ≤ l₂;

(∆∂ = ∆x / v)

同时假设：
- q(0) = aH₀;（香烟毒物被吸入的量）
- H₀ = uw₀;（香烟毒物的减少量）
可得到

dq/dx = -b/v * q(x), 0 ≤ x ≤ l₁;

dq/dx = -ß/v * q(x), l₁ ≤ x ≤ l₂;

&

q(x) = aH₀e^-bx/v, 0 ≤ x ≤ l₁;

q(x) = aH₀e^-bx/ve^-ß(x-l1)/v, l₁ ≤ x ≤ l₂;
目标是求q(l, t)，假设t时刻，香烟燃烧到了x = ut；

将q(x)中的H₀拓展为H(t)，x随时间会变成x-ut，l₁会变成l₁ - ut

可以求得：

q(x, t) = aH(t)e^-b(x-ut)/v,ut ≤ x ≤ l₁;

q(x, t) = aH(t)e^-b(l1-ut)/ve^-ß(x-l1)/v,l₁ ≤ x ≤ l;
求w(ut, t)求∆t内毒物密度的增量。
w(x, t + ∆t) - w(x, t) = b(q(x, t))/v * ∆t（单位长度烟雾被吸收的部分）

我们已知：
- q(x, t) = aH(t)e^-b(x-ut)/v;
- H(t) = uw(ut, t);（H₀的拓展公式）
结果可得到：

w(ut, t) = w₀/a’ * (1 - ae^-a’but/v), a’ = 1 - a;
计算Q，吸入一致烟毒物进入人体的总量；

根据求出来的 w(x, t) 和 q(l, t) 可以代入Q = ƒ₀^T q(l, t)dt, T = l₁ / u;求出现在的Q = aM e^-ßl2/v µ®, r = a’bl₁/v, µ® = 1 - e^-r / r;

结果分析：

Q和a，M成正比，aM是毒物集中在x = l处的吸入量；
e^-ßl2/v是过滤嘴的因素；
µ®是烟草的吸收作用；
判断与不带过滤嘴的香烟比较
Q₁和Q₂的差别为b和ß；

我们已知：
- 带滤嘴：Q₁ = (aw₀v / a’b) e^-ßl2/v(1 - e^-a’bl1/v);
- 不带滤嘴：Q~12 = (aw₀v / a’b) e^-bl2/v(1 - e^-a’bl1/v);
所以明显是滤嘴提高了吸收能力

特点：

引入两个基本函数：流量q(x,t)和密度w(x,t)，运用物理学的守恒定律建立微分方程，构造动态模型。

3. 偏微方程的导出

3.1. 波动方程的导出

传输线方程（电报方程）
均匀薄膜的微小横振动方程
流体力学与声学方程
电磁波方程

ta们的物理本质根本不同，但这些方程的数学形式与弦振动方程和杆纵振动方程完全一样：

3.2. 扩散方程的导出

3.2.1. 细杆热传导

现象描述：导热细杆各点的温度是不均匀的，热量由高到低传导。

目的：求出细杆中温度的变化方程。

定律：

热传导的傅立叶定律：q = -k∆u（单位时间内流过单位时间的热量q与温度的梯度成正比，k为热传导系数）；
热量守恒定律：热量变化 = 边界流入 + 热源放出；

第一种情况（系统无热源）：

（热传导仅由物体内部温度不均引发）

u(x, t)为x处t时刻的温度。

一维情况下热传导的傅立叶定律有： q = -k∂u/∂x;（q为热流强度）

在x方向上（微元法）：

dt时间流入左表面的热量为：q|_x Adt;
dt时间流出右表面的热量为：q|_x+dx Adt;
所以净流入为：q|_x Adt - q|_x+dx Adt = -∂q/∂xAdxdt =（然后把q换掉再整合）= ku_xxAdxdt;

因为热量Q = c(øAdx)[u|_t - u|_t+dt] = c(øAdx)u_tdt;（假设ø为密度）

所以更具热量守恒定律得到ku_xxAdxdt = c(øAdx)u_tdt；

结果：u_t - a²u_xx = 0, a² = k/cp（这就得到了均匀物体内部无热源时的热传导方程）

第二种情况（系统内有热源）：

比第一问不过就是多个热源，也就是加一个热量呗（设F(x, t)为单位时间，单位体积内产生的热量：ku_xxAdxdt + F(x, t)Adxdt = c(øAdx)u_tdt;

得到：u_t - a²u_xx = F(x, t) / cp = f(x, t)；（ƒ(x, t)为热源强度）

三维情况下就是：u_t - a²∆u = f(x, t)；

3.2.2. 扩散问题

扩散现象：系统浓度不均用时，物质从高浓度转移向低浓度的现象。

目的：建立空间各点浓度u(x, y, z, t)的方程。

物理规律：扩散定律和粒子数守恒定律

扩散定律（裴克定律）：单位时间内流过单位面积的分子数或质量，与浓度的梯度成正比：（D为扩散系数）

沿着n方向的大小：
粒子数守恒定律：单位时间流入一定体积粒子数与流出同一体积粒子数的差，等于该体积单位时间内粒子数的增加量。
同样是微元法，划出一个小立方体v分析浓度变化规律。
- 计算单位时间沿x-方向的净流入量（负号是表示和浓度梯度的方向相反）：（利用两个平面的流入流出的积分）
- 同理可以求出y方向和z方向的净流入量：
- 所以总的净流入量为
- 单位时间的粒子增加数为：
- 根据粒子数守恒定律就可以得到：
我们在前面得到过这样的结果：和

所以我们将扩散定律代入就可以得到三维扩散方程：

我们484看到了吗有很多D，如果扩散是均匀的，D就是一个常数，我们可以令D = a²，则有

那如果这个空间里面有扩散源，也就是扩散是从这儿来的，那么我们可以将ta们相等得到公式：

3.3. 稳定场方程

3.3.1. 热传导方程

如果边界条件与热源内不随时间变化，一定时间后，内部温度会达到稳态。

u = u(x, y, z), ∂u/∂t = 0;

so

u_t - a²∆u = f(x, y, z, t) -> ∆u = -f(x, y, z)泊松方程

3.3.2. 静电场下的泊松方程和Laplace方程

从高斯定理出发，我们可以结合扩散定律简单的得到：

我们可以得到

还因为

我们可以得到两个方程：

泊松方程：
Laplace方程（当的时候）：

4. PDE导出总结

系统的物理状态除了取决于自己状态，还取决于系统环境的状态。

物理、工程在t>0时刻的系统环境，在数学中称为边界条件；
物理、工程在t=0时刻的系统状态，在数学中称为初始条件；

定解条件：是边界条件和初始条件的总体，反映了问题的个性。

泛定方程：不带边界和初始条件的方程，反映问题的个性。

4.1. 初始条件 ——描述系统的初始状态

波动方程：含有时间的二阶导数，所以需要两个初始条件
1. u|_t=0 = u(x) 系统各点的初始位移
2. ∂u/∂t|_t=0 = v(x) 系统各点的初始速度
热传导方程：含有时间的一阶导数
1. u(x, t)|_t=0 = u(x)初始时刻的温度分布
泊松方程和拉普拉斯方程：不含时间的倒数，不需要初始条件

注意：初始条件给的是初始状态下物理量的分布，而不是指某一位置

4.2. 边界条件

未知函数在边界满足条件：

第一类Dirchlet边界条件：已知未知函数在边界上的函数值：

基本形式：u(x, y, z, t)|_∑ = ƒ(M, t);
第二类Neumann：已知未知函数在边界上法线方向的导数值；
基本形式：∂u(x, t)/∂n|_x0 = ƒ(x₀, t);
第三类Robin混合边界条件：混合牛顿冷却定律、傅立叶实验定律（一维）；

牛顿冷却定律：

q = h(u - ø)n，u为物体表面温度，ø是周围介质温度，h是热交换系数。一维条件下简化为q = h(u - ø)。

牛顿冷却定律可以得出流出热量与外界温差成正比。

傅立叶实验定律：

q|_x=a = -k∂u/∂x|_x=a

基本形式：(u + H∂u/∂n)|_∑ = ƒ(x₀, y₀, z₀, t);