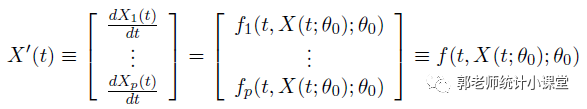目录

一、模型的建立

传染病模型概念

模型假设

SEIR模型

模型中涉及的函数S(t)、E(t)、I(t)、R(t)

更改后的微分方程

二、模型的求解

三、模型的缺点

祝语

---

随着疫情的再次爆发，全国疫情防控再次进入紧张状态，疫情预测分析成为数学建模问题中的一个热点问题，本文基于微分方程的SEIR模型对疫情做出简单预测。

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、模型的建立

传染病模型概念

   传染病基本数学模型主要是研究传染病的动力学原理、传播方式、空间范围、传播速度等问题。常见的传染病模型按传染病类型分为SI、SIR、SEIR模型等，对疫情的研究，本文选取SEIR模型，相比较SIR模型，能更好的预测疫情变化趋势。

模型假设

1.假设初始时刻易染者为总数N

2.假设病毒时间尺度远小于个体生命周期，即不考虑个体自然出生率和自然死亡率

3.建设各个个体间接触机会均等

SEIR模型

假设人群总体为N，定义四类人群，如下表所示。

                                                                表1  SEIR 模型的符号定义

符号	名称	解释
S	易染者	健康状态，可被感染的个体
E	暴露者	即与感染者接触过的个体（潜伏期）
I	感染者·	处于感染状态的个体还能够感染将康状态的个体
R	治愈者	恢复状态

在病毒最开始的时候S=N，然后S以每天α的速度变到E，E以每天σ的速度变到I,I又以每天β的速度变到R：

        

SEIR模型对应的经典微分方程为：
                                                             

                                   

                                                              

                                                              

                                                

模型中涉及的函数S(t)、E(t)、I(t)、R(t)

  S(t)的意思是第t天健康个体的数量，E(t)是第t天接触过感染者的个体数量，I(t)是第t天感染个体的数量，R(t)是第t天免疫个体的数量，N(t)是整个种群的数量，在假设情况下固定不变为N，取。

  该模型为经典传染病模型，由于疫情感染因素较普通传染病较为复杂，且具有潜伏期，因此引入三个额外的参数，，a.，,a分别为潜伏期自愈转化为康复者，即接触过感染者但未被感染，患病者治愈后转为康复者的概率,潜伏者对易感人群的传染率。

更改后的微分方程

                                                              

                                                                   

                                                      

                                                      

                                                      

二、模型的求解

         对于模型的求解，我们需要拟合六个参数：即易感者初始值S(0)，潜伏者初始值E(0)，传染率β，潜伏率a，康复率。查找近七天的数据，运用MATLAB拟合工具箱对数据进行拟合。

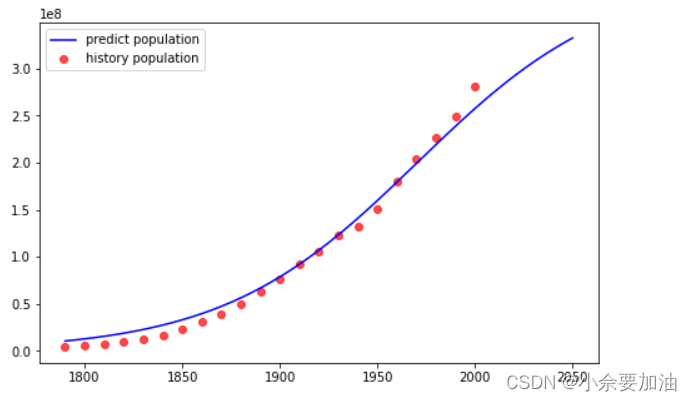
     图1 全国4月10至16日确诊人数及拟合

---

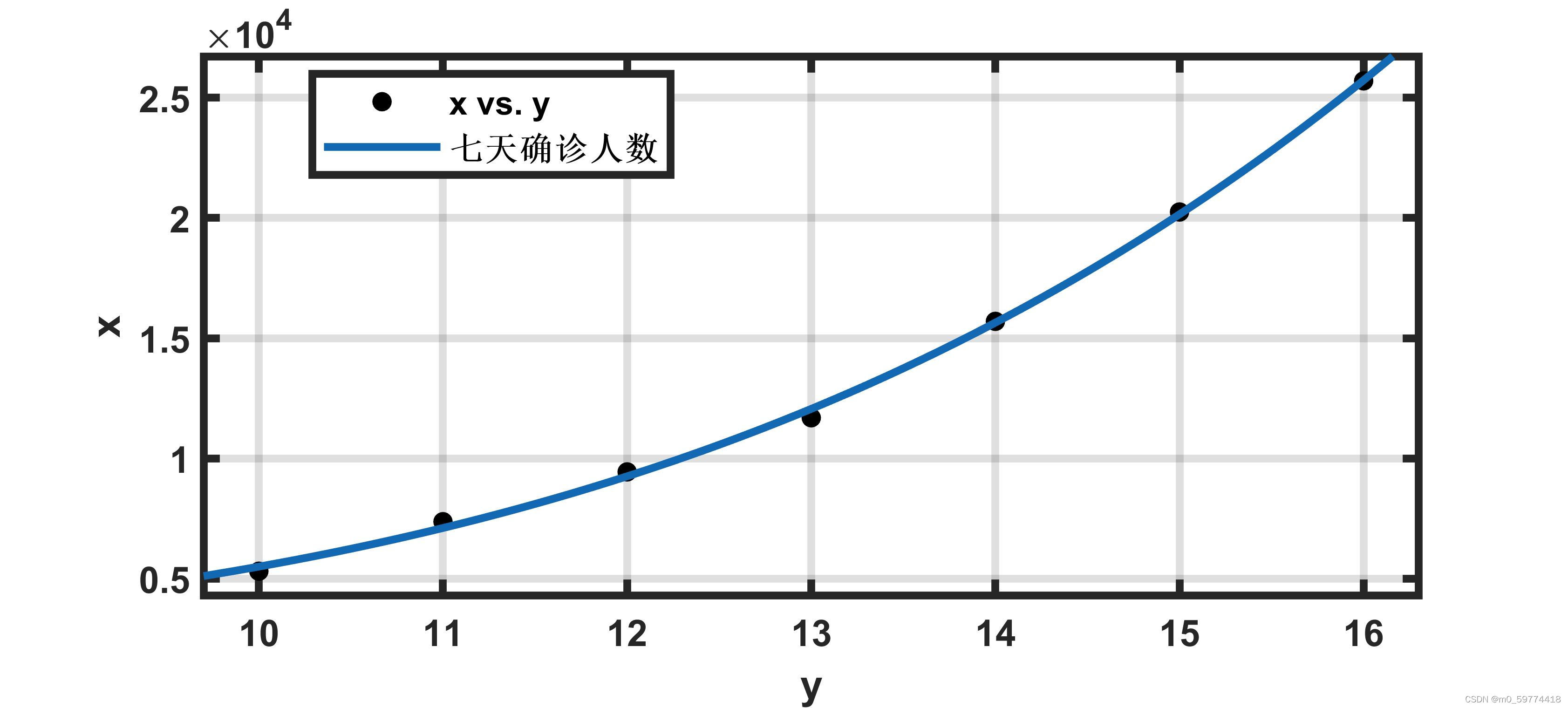
得到I(t)的拟合表达式：

                                                         

继而得出：

                                                                    

下面拟合近七天的治愈人数：

                                                                   图二 近七天治愈人数

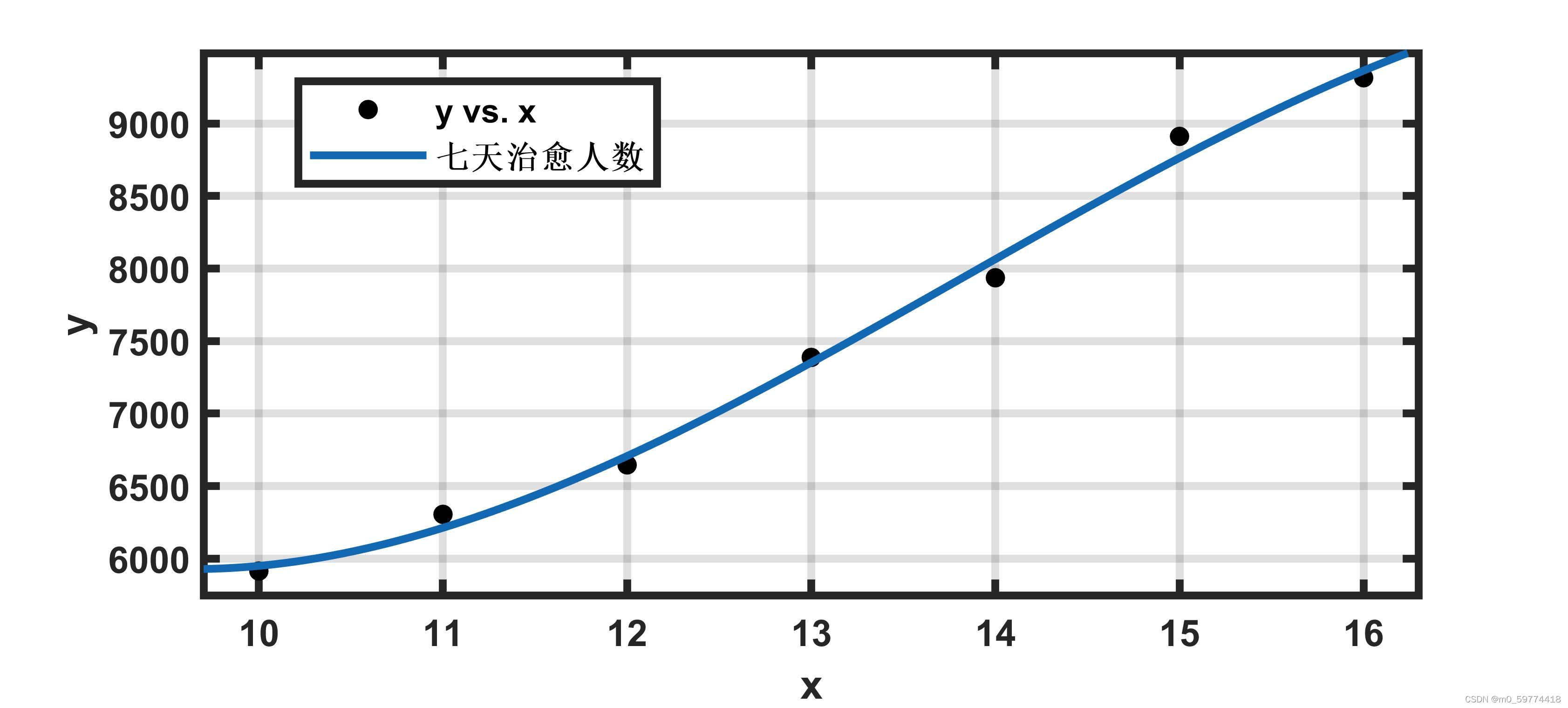
 可以看到拟合效果不佳，可能由于科技，防控和疫情变化因素均很大，我们缩短时间尺度

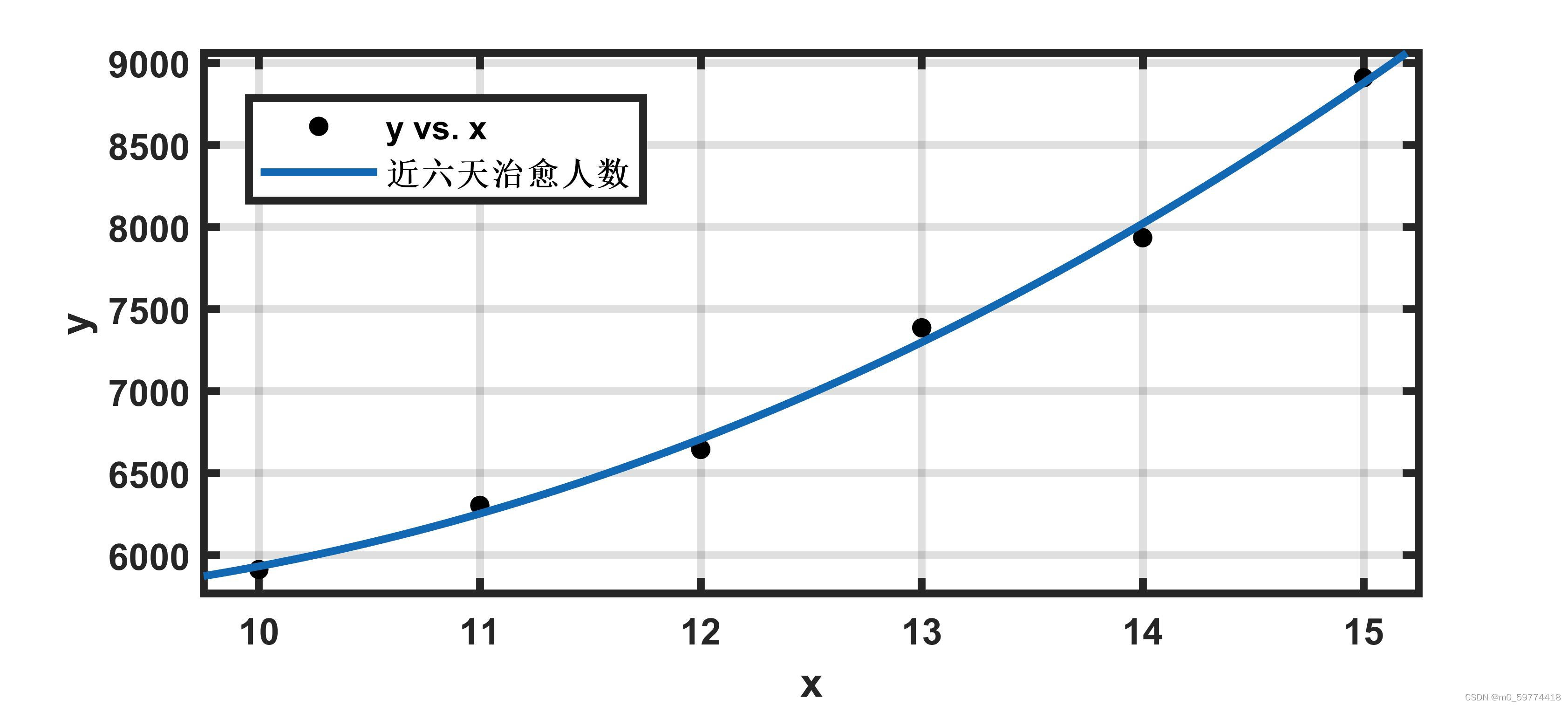
 可以看到近六天的拟合效果明显好于近七天的，得出R(t)的函数表达式：

                                                                            

                                                                             

    原方程组化为：

                                                                                       

                                                                  

                                                                               

                                                                        

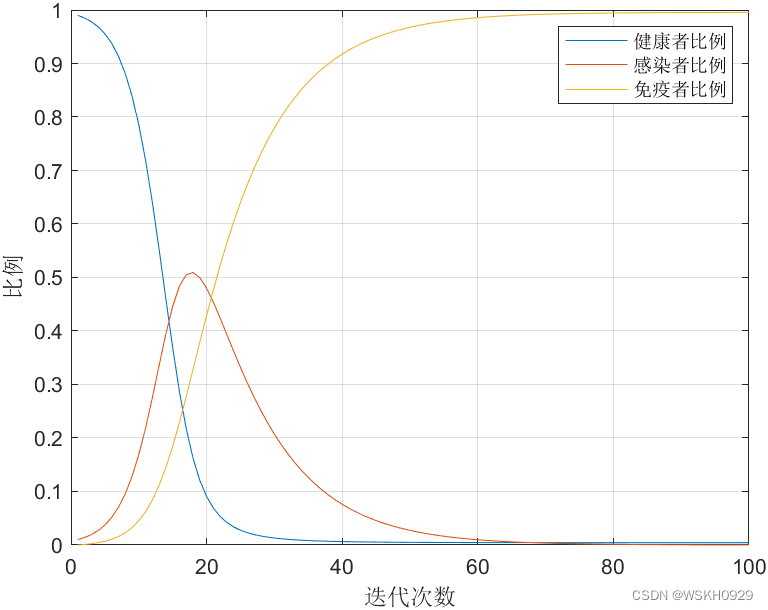
    最后用MATLAB编程计算得出结果：         

                                                                                 

                                                                                  

                                                                                   

                                                                                   

                                                                                     a=0.05

                                                                       

        MATLAB得出最终预测结果：

 

 

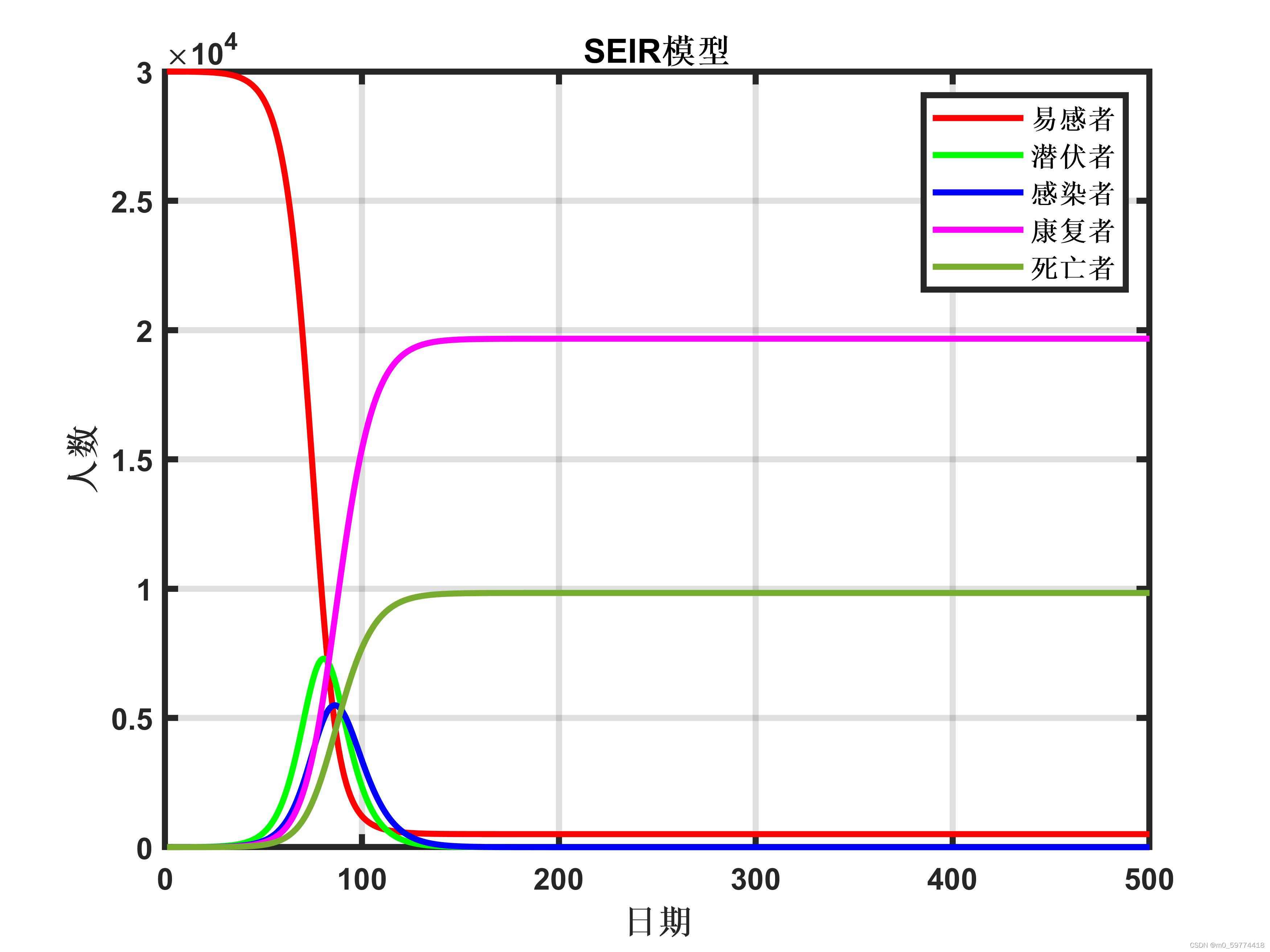
三、模型的缺点

1.在SIR模型的基础上，SEIR模型在模型中加入了E, 具有潜伏期且潜伏期不具有传染性传染病适用 SEIR模型。新型冠状病毒在潜伏期也具有传染性，并不满足SEIR模型的适用条件，因此该模型存在较大局限性

2.疫情传播过程中人与人之间的接触机会并不均等

祝语

  新型肺炎看出人生百态，是对政府、民众、科研工作者最大的考题。第一时间公开数据信息、治疗方案、数理模型、预测结果等，是科研人最大的贡献。面对谣言和恐慌，科学分析、知识传递，也尤为重要。相信全国齐心协力，必能获得抗击新型肺炎的最终胜利。