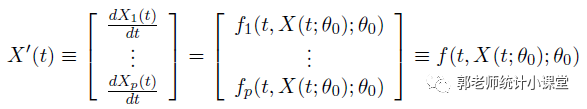微分方程模型
短、中、长期的预测都适合。
反应事物内部规律及其内在关系,但由于方程的建立是以局部规律的独立性假定为基础,当作为长期预测时,误差较大,且微分方程的解比较难以得到。
具体案例
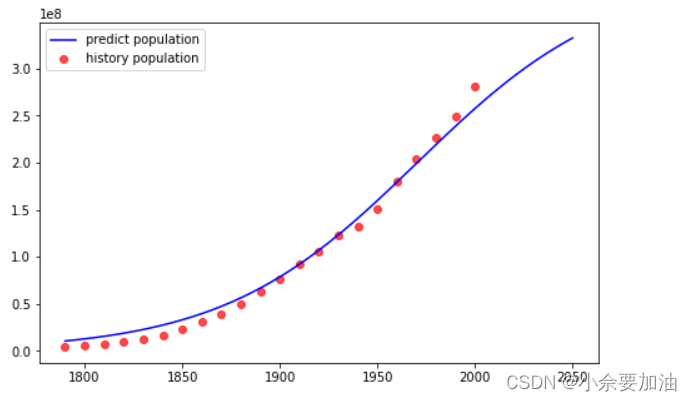
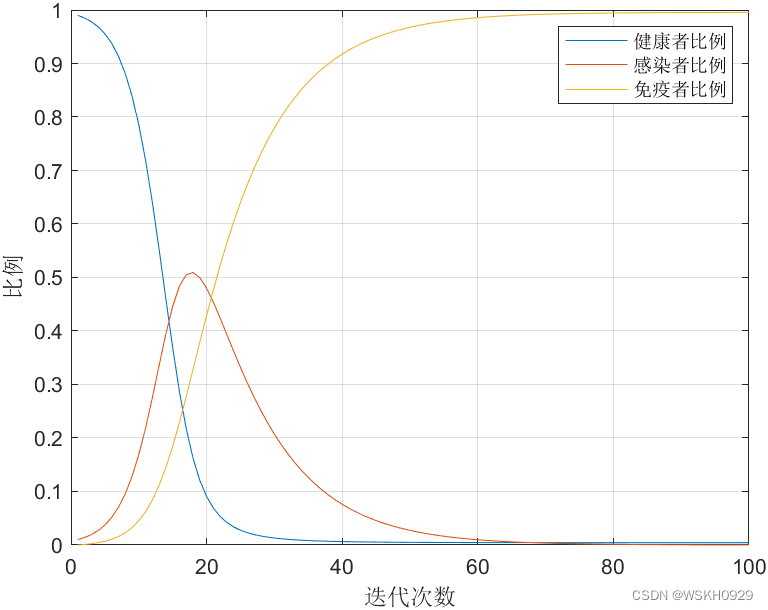
传染病的预测模型、经济增长(或人口)的预测模型、Lanchester战争预测模型、药物在体内的分布与排除预测模型、烟雾的扩散与消失模型
列微分方程的常用方法
直接列方程
- 利用所学过的公式对某些实际问题列出微分方程。
微元分析法与任意区域上取积分的方法
- 利用已知的规律建立一些变量(自变量与未知函数)的微元之间的关系式。
- 然后再通过取极限的方法得到微分方程,或等价地通过任意区域上取积分的方法来建立微分方程。
模拟近似法
- 在一定的假设下,给出实际现象所满足的规律,然后利用适当的数学方法列出微分方程。
- 在实际的微分方程建模过程中,也往往是上述方法的综合应用。不论应用哪种方法,通常要根据实际情况,作出一定的假设与简化,并要把模型的理论或计算结果与实际情况进行对照验证,以修改模型使之更准确地描述实际问题并进而达到预测预报的目的。
MATLAB求解方法
dsolve()函数
[y1,y2,⋯,yn]=dsolve(eqns,conds,name,value)
其中:eqns为符号微分方程(组);conds为初值条件或边值条件;name,value为可选的成对参数。

>> y1=dsolve('Dy=1+y^2','y(0)=1','x')
>> [x,y]=dsolve('Dx=y,D2y-Dy=0','x(0)=2,y(0)=1,Dy(0)=1','t')
利用ode函数
还有大量的常微分方程,虽然从理论上讲,其解是存在的,但我们却无法求出其解析解,此时,我们需要寻求方程的数值解。
function testode45
tspan=[3.9 4.0]; %求解区间
y0=[8 2]; %初值
[t,x]=ode45(@odefun,tspan,y0);
plot(t,x(:,1),'-o',t,x(:,2),'-*')
legend('y1','y2')
title('y'' ''=-t*y + e^t*y'' +3sin2t')
xlabel('t')
ylabel('y')
function y=odefun(t,x)
y=zeros(2,1); % 列向量
y(1)=x(2);
y(2)=-t*x(1)+exp(t)*x(2)+3*sin(2*t); %常微分方程公式
end
end