微分方程模型

article/2025/10/10 22:32:55

微分方程模型简介

在研究生物、经济等学科的实际问题时，常常会联系到某些变量的变化率或导数，这样所得到变量之间的关系式就是微分方程。微分方程反映的是变量之间的间接关系，因此，要得到直接关系，就得求解微分方程。

1.微分方程建模分类：

静态优化模型
存储模型，价格模型，消费者均衡模型

动态模型
人口模型,传染病模型

描述对象特征随时间（空间）的演变过程
分析对象特征的变化规律
预报对象特征的未来性质
研究控制对象特征的手段

稳态模型
种群的竞争模型，军备竞赛模型

2.建立微分方程模型的方法

翻译或转化
在实际问题中许多表示导数的常用词，如“速率”、‘增长”(在生物学以及人口问题研究中)，“衰变”(在放射性问题中)，以及“边际的”(在经济学中)等。

建立瞬时表达式
根据自变量有微小改变△t时，因变量的增量△W，建立起在时段△t上的增量表达式，令△t →0，即得到 dw/dt 的表达式。

配备物理单位
在建模中应注意，一旦确定了哪些子项应该列入微分方程中，就要确保每一项都采用同样的物理单位，以保证式子的平衡。

确定约束条件
约束条件是关于研究对象在某一特定时刻或边界上的信息（比如初始时刻），它们独立于微分方程而存在，用以确定有关的常数（比如比例系数、解中的积分常数、方程参数）。为完整充分地给出问题的数学陈述，应将这些约束条件和微分方程一起列出。

引例（体重问题）：

某人的食量是10467（焦／天)，其中5038(焦／天)用于基本的新陈代谢(即自动消耗)。在健身训练中，他所消耗的热量大约是69(焦／公斤*天）乘以他的体重 (公斤)．假设以脂肪形式贮藏的热量100%地有效，而1公斤脂肪含热量41868焦。
试研究此人的体重随时间变化的规律．

1模型分析
问题中并未出现“变化率”、“导数”等关键词，但要寻找的是体重（记为W）关于时间（记为t）的函数。如果把W看成是t的连续可微函数，则就找到了一个含有 dw/dt 的微分方程。

2模型假设
（1）以W(t)表示t时刻某人体重，并设一天开始时人的体重为W0 。
（2）体重的变化是一个渐变的过程。因此可以认为W(t)是关于连续t而且充分光滑的。
(3）体重的变化等于输入与输出之差，其中输入是指扣除了基本新陈代谢之后的净食量吸收；输出是进行健身训练时的消耗。

3模型建立
1、“每天”：体重的变化／天=净吸收量／天一净输出量／天，其中：
净吸收量／天＝10467-5038 ＝5429（焦／天）
净输出量／天＝69(焦／公斤·天)×W(公斤）
＝69W(焦／天)

体重的变化／天＝△w/△t(公斤／天)=△t->0 dw/dt （微元分析法）

4配备物理单位
有些量是用能量(焦)的形式给出的，而另外一些量是用重量的形式(公斤)给出，已知1公斤脂肪含热量41868焦，考虑单位的匹配，有：
在这里插入图片描述

5建立瞬时表达式：
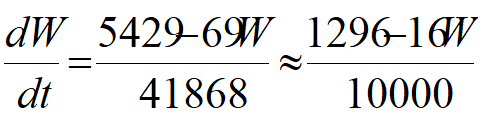
在这里插入图片描述

6确定约束条件：
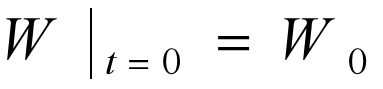
在这里插入图片描述

模型求解
利用变量分离法求解可得：
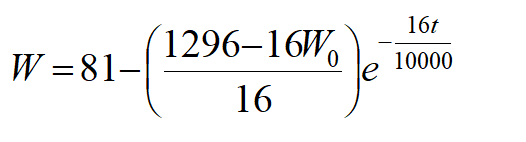
在这里插入图片描述

用MATLAB求解引例的解析解

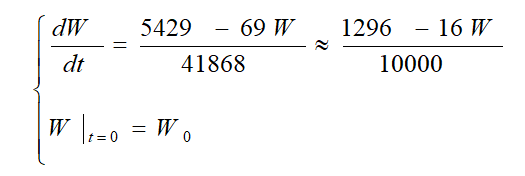
在这里插入图片描述

输入命令：dsolve(‘DW=1296-16W/10000’, ‘W(0)=W0 ’,‘t’)
结果为：81+exp(-1/625t)(-81+W0)

求解微分方程模型的方法

求解析解（精确解）；
dsolve(‘方程1’,‘方程2’,…,‘方程n’,‘初始条件’,‘自变量’)
例题：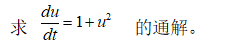

解输入命令：dsolve(‘Du=1+u^2’,‘t’)
结果为：u = tan(t+c1)

例题2：
求微分方程的通解。
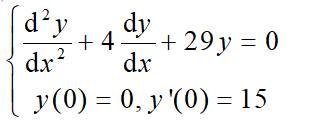
在这里插入图片描述

解输入命令:
y=dsolve(‘D2y+4Dy+29y=0’,‘y(0)=0,Dy(0)=15’,‘x’)
结果为: 3exp(-2x)sin(5x)

求数值解（近似解）；

在生产和科研中所处理的微分方程往往很复杂,且大多得不出一般解．而实际中的初值问题，一般是要求得到解在若干个点上满足规定精确度的近似值，或者得到一个满足精确度要求的便于计算的表达式。因此，研究常微分方程的数值解法是十分必要的。

对常微分方程:y’=f(x,y) y(x0)=y0 ,其数值解是指由初始点x0开始的若干离散的x处的值，即对x0<x1<x2<…<xn，求出准确值y(x1) ,y(x2)…y(xn)的相应近似值y1,y2…yn。

定性理论方法。

实例2.人口模型

人口问题是当今世界上最令人关注的问题之一，一些发展中国家的人口出生率过高，越来越威胁着人类的正常生活，有些发达国家的自然增长率趋于零，甚至变为负数，造成劳动力紧缺，也是不容忽视的问题。另外，在科学技术和生产力飞速发展的推动下，世界人口以空前的规模增长，统计数据显示：
世界人口统计：
在这里插入图片描述
我国人口统计：

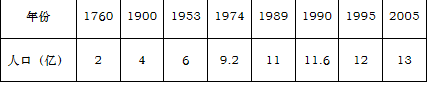
问题的提出：
人口在不断的增长，其增长有无规律可循？
目标：预测人口发展趋势；控制人口增长。

建立模型：

1、简单模型

要预报未来若干年的人口数，两个重要因素：
当前的人口数x0、年增长率r（出生率-死亡率）
一年后，人数增加到：x1=x0+x0*r=x0(1+r)
k 年后，人口数为：xk=x0(1+r)^k

2、Malthus 模型(指数增长模型)

Malthus(1766–1834)是英国的人口学家。他根据百余年的人口统计资料，于1798年提出著名的人口指数增长模型。

模型假设：
人口净相对增长率为常数r、净相对增长率是单位时间内的人口的增长量占当时的人口总数的比例、t时刻人口总数为N(t)、把N(t) 当作连续的变量
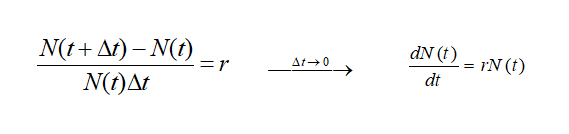
在这里插入图片描述

Malthus 模型：

在这里插入图片描述

模型求解：

在这里插入图片描述

模型分析：

（1）数据表明，在1700—1961年期间，世界人口吻合较好。在此期间，人口约35年增长一倍。
（2）若r>0，人口以指数规律无限增长，t→∞时，N(t)→+∞.这似乎不太可能。
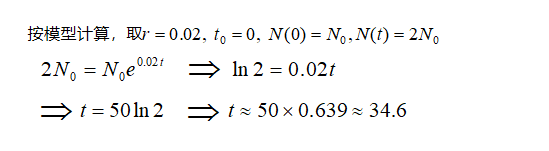
在这里插入图片描述

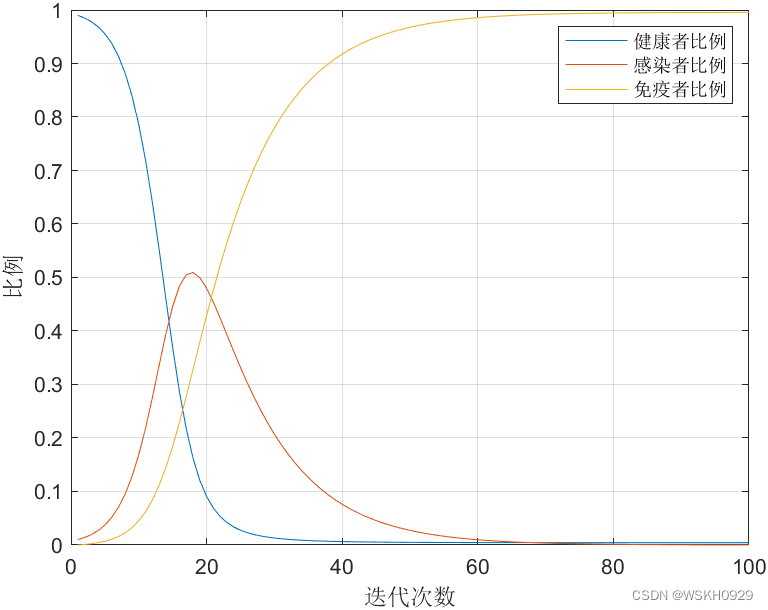
3、Logistic模型（阻滞增长模型）

**模型假设：**人口相对增长率随人口的增加而线性减少。
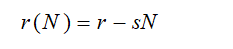
在这里插入图片描述

**模型的建立：

**
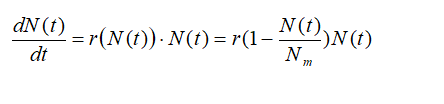
这是一个非齐次常微分方程

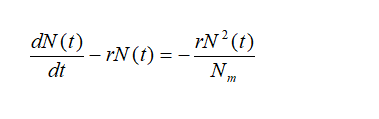
容易求得其齐次常微分方程：

模型的求解
在这里插入图片描述

结论：在人口总数达到极限值Nm的一半以前是加速生长期，过了这一点以后，生长率逐渐减小，并且趋于零。

4、Leslie模型（按年龄分布的离散人口增长模型）

-------差分方程模型

模型假设：
(1)时间离散化,设男女人口的性别比例为1:1。因此模型仅需考虑女性人口的发展变化。假设女性最大年龄为S岁，将其等间隔分成m个年龄段(年龄离散化),设S为m的整数倍,每隔S/m年观察一次(时间离散化),不考虑同一时间间隔内人口数量的变化；
(2)记ni(t)为第i个年龄组t次观察的女性总人数,记
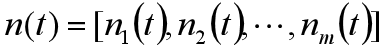
在这里插入图片描述