---

一、学习内容

1. 微分方程基本概念
2. 微分方程在数学建模中的应用
3. 微分方程常用模型（人口增长模型、传染病模型）

---

二、学习时间

2022.06.19

---

三、学习产出

3.1 微分方程基本概念

微分方程，是指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。

微分方程是伴随着微积分学一起发展起来的。微积分学的奠基人Newton和Leibniz的著作中都处理过与微分方程有关的问题。微分方程的应用十分广泛，可以解决许多与导数有关的问题。物理中许多涉及变力的运动学、动力学问题，如空气的阻力为速度函数的落体运动等问题，很多可以用微分方程求解。此外，微分方程在化学、工程学、经济学和人口统计等领域都有应用。

数学领域对微分方程的研究着重在几个不同的面向，但大多数都是关心微分方程的解。只有少数简单的微分方程可以求得解析解。不过即使没有找到其解析解，仍然可以确认其解的部分性质。在无法求得解析解时，可以利用数值分析的方式，利用电脑来找到其数值解。 动力系统理论强调对于微分方程系统的量化分析，而许多数值方法可以计算微分方程的数值解，且有一定的准确度。

简单来说，微分方程指的是：含有未知函数及其导数的方程。，下面是几种微分方程的例子：

非齐次一阶常系数线性微分方程：

齐次二阶线性微分方程：

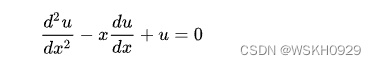
非齐次一阶非线性微分方程：

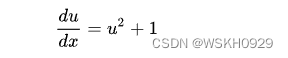
3.2 微分方程在数学建模中的应用

问题描述：
某人每天由饭食获取2 500卡热量，其中1 200卡用于新陈代谢，此外每千克体重需支付16卡热量作为运动消耗，其余热量则转化为脂肪，已知以脂肪形式贮存的热量利用率为100%，每千克脂肪含热量10 000卡，问此人的体重如何随时间而变化？

解析：
设人的体重为m（t），假设体重随时间是连续变化的，即m（t）是连续函数且充分光滑，故我们认为能量的摄取和消耗是随时发生的.这里我们以“天”为时间单位，在任何一个时间段内考虑能量的摄入和消耗所引起的体重的变化.根据能量的平衡原理，任何时间段内由于体重的改变所引起的人体内能量的变化应该等于这段时间内摄入的能量与消耗的能量的差.

我们发现从理论上来说，只要适当调节A和B，C（不变），即控制饮食和增加活动量，减肥就能达到好的效果.

3.3 微分方程常用模型

3.3.1 人口增长模型

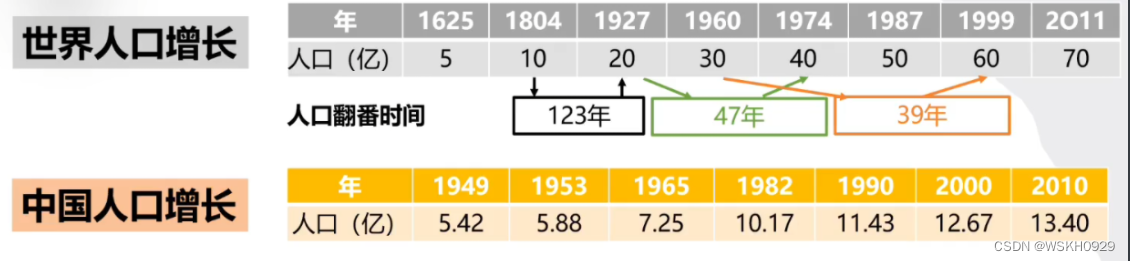
图片来源：【微分方程模型】【2021国赛赛前培训】

3.3.1.1 指数增长模型(马尔萨斯模型)

所谓指数增长模型，就是假设人口是随着一个固定的增长率不断增长。此模型由马尔萨斯1798年提出，故又称为马尔萨斯模型。下面是有关指数增长模型公式的推导和演示：

• 假设t时刻人口数量为连续、可微函数x(t)
• 假设单位时间人口增长率为常数r
• 假设初始人数为x0
  
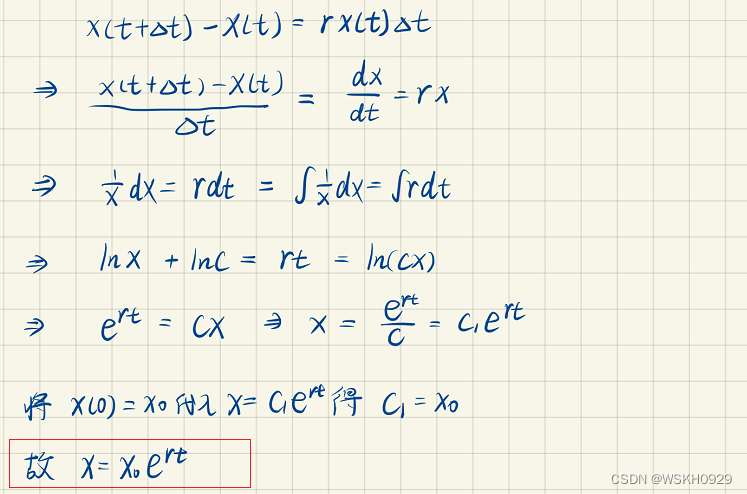
  Matlab代码：

% 人口增长-指数增长模型
% 清空工作区和变量区
clear;clc;
% 定义迭代次数
n = 250;
% 定义并初始化参数
x = zeros(1,n);
x(1,1) = 5.42; % 初始化人口数(亿)
r = 0.018; % 人口增长率
% 开始迭代
for t = 2:nx(1,t) = x(1,1)*exp(r*t);
end
% 绘图
plot(1:1:n,x);
legend('人口增长曲线');
xlabel('迭代次数');
ylabel('人口数（亿） ');
grid on;

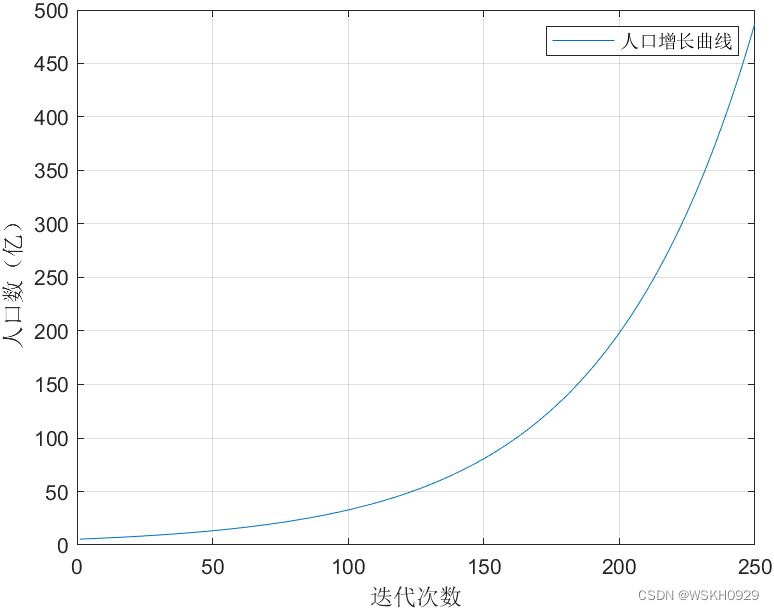
从上图，我们可以明显地看出指数增长模型存在以下几点局限性：

• 不符合多数地区人口增长规律。
• 实际上只有在群体总数不太大时才合理，当总数增大时，生物群体的各成员之间由于有限的生存空间，资源，食物等原因可能发生竞争的情况。
• 人口净增长率不可能始终保持常数，它应当与人口数量有关。

3.3.1.2 阻滞增长模型(Logistic模型)

阻滞增长模型对指数增长模型进行了改善，即考虑了资源、环境等因素对人口增长的阻滞作用，且阻滞作用随人口的增加而变大。下面是有关阻滞增长模型公式的推导和演示：

• 假设t时刻人口数量为连续、可微函数x(t)
• 假设单位时间人口增长率为x的减函数，即r(x)=a-bx，其中b>0
• 假设当前环境和资源最大可能承受的人口数为xm
• 假设r(0)=r，r(xm)=0，其中r为一个常数，即初始人口增长率
• 假设初始人数为x0

Matlab代码：

% 人口增长-阻滞增长模型
% 清空工作区和变量区
clear;clc;
% 定义迭代次数
n = 500;
% 定义并初始化参数
x = zeros(1,n);
x(1,1) = 5.42; % 初始化人口数(亿)
r = 0.018; % 初始人口增长率
xm = 100; % 最大人口数
% 开始迭代
for t = 2:nx(1,t) = xm/(1+(xm/x(1,1)-1)*exp(-r*t));
end
% 绘图
plot(1:1:n,x);
legend('人口增长曲线');
xlabel('迭代次数');
ylabel('人口数（亿） ');
grid on;

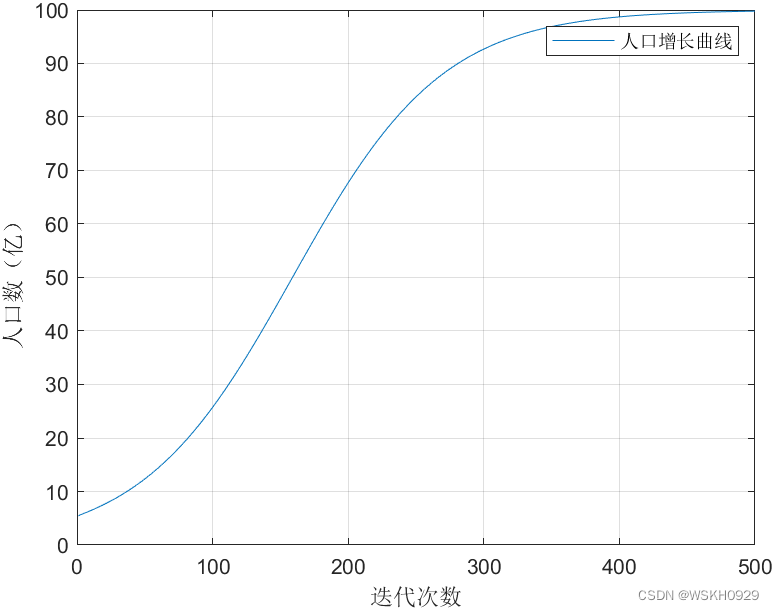
3.3.1.3 人口模型小结

• 指数增长模型和Logistic模型（阻滞增长模型）均为对微分方程所作的模拟近似方程。
• 前一模型假设了增长率为一常数，后一模型则假设环境只能供养一定数量的种群，从而引入了上个竞争项
• 指数增长模型呈现的是J型增长，只适应于短期内，并没有考虑外界因素的影响。
• Logistic模型呈现S型，适应于中长期且有外界因素影响。

---

3.3.2 传染病模型

• 描述传染病的传播过程
• 分析受感染人数的变化规律
• 预报传染病高发期到来的时刻
• 按照传播过程的一般规律，用机理分析方法建立模型

3.3.2.1 SI模型

SI模型将人群分为两类，一类是健康人群（S），另一类是感染者（I）

• 假设总人数为N，且N不变
• 假设时刻t健康人和感染者所占比例分别为s(t)和i(t)，且s(t)+i(t)=1
• 假设每个病人每天有效接触人数为L（日接触率），感染者接触健康者，就会让健康者患病
  
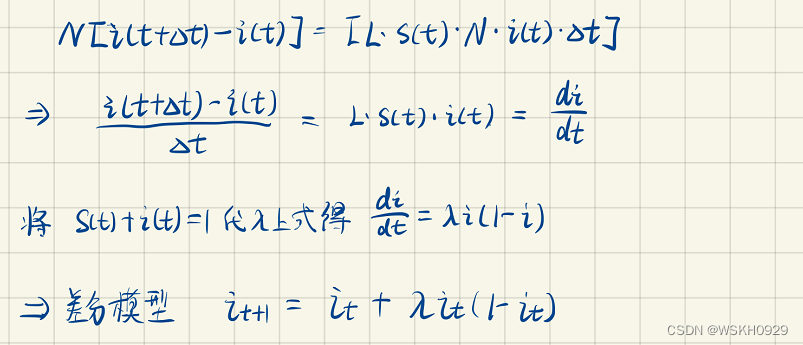
  Matlab代码：

% 传染病SI模型
% 清空工作区和变量区
clear;clc;
% 定义迭代次数
n = 100;
% 定义并初始化状态E(s,i)
E = zeros(2,n);
E(1,1) = 0.99; % 初始健康者比例
E(2,1) = 0.01; % 初始感染者比例
% 初始化参数
L = 0.5; % 病人日接触率
% 开始迭代
for t = 1:n-1E(2,t+1) = E(2,t) + L*E(2,t)*(1-E(2,t));E(1,t+1) = 1 - E(2,t+1);
end
% 绘图
s = E(1,:); % 健康者比例数据
i = E(2,:); % 感染者比例数据
plot(s,'DisplayName','s');hold on;
plot(i,'DisplayName','i');
legend('健康者比例','感染者比例');
xlabel('迭代次数');
ylabel('比例');
grid on;
hold off;

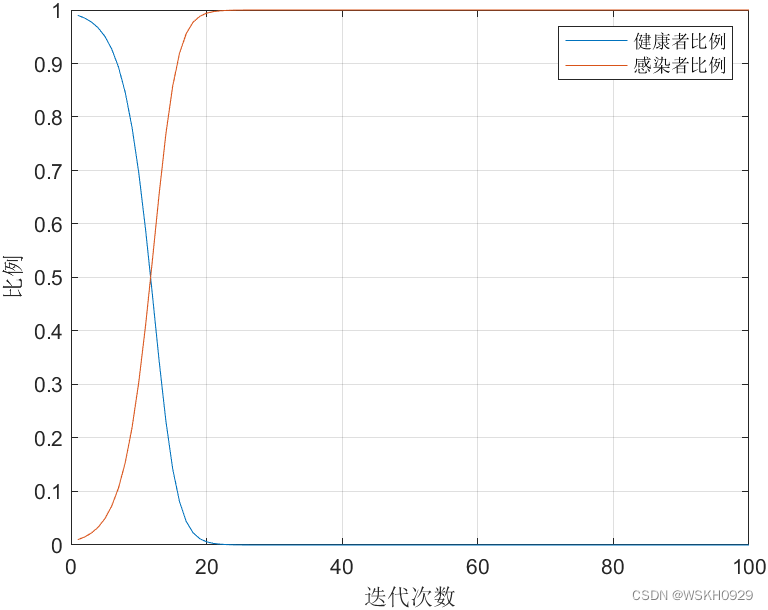
SI模型的缺点在于，没有考虑病人可以被治愈的情况，导致最后所有健康者都会变为感染者，不太符合实际情况

3.3.2.2 SIS模型

SIS模型在SI模型的基础上，还考虑了健康人被感染后可能会被治愈，而且治愈后，还可能再次被感染的情况

• 假设总人数为N，且N不变
• 假设时刻t健康人和感染者所占比例分别为s(t)和i(t)，且s(t)+i(t)=1
• 假设每个病人每天有效接触人数为L（日接触率），感染者接触健康者，就会让健康者患病
• 假设病人每天的治愈率为M（日治愈率）
  
  Matlab代码：

% 传染病SIS模型
% 清空工作区和变量区
clear;clc;
% 定义迭代次数
n = 100;
% 定义并初始化状态E(s,i)
E = zeros(2,n);
E(1,1) = 0.99; % 初始健康者比例
E(2,1) = 0.01; % 初始感染者比例
% 初始化参数
L = 0.5; % 病人日接触率
M = 0.2; % 病人日治愈率
% 开始迭代
for t = 1:n-1E(2,t+1) = E(2,t) + L*E(2,t)*(1-E(2,t))-M*E(2,t);E(1,t+1) = 1 - E(2,t+1);
end
% 绘图
s = E(1,:); % 健康者比例数据
i = E(2,:); % 感染者比例数据
plot(s,'DisplayName','s');hold on;
plot(i,'DisplayName','i');
legend('健康者比例','感染者比例');
xlabel('迭代次数');
ylabel('比例');
grid on;
hold off;

SIS模型作为SI模型的升级版，考虑了病人被治愈的情况，但同时，SIS模型没有考虑病人被治愈后，可能会产生抗体，而不会被再次感染的情况，不太符合某些传染病的模拟

3.3.2.3 SIR模型

SIR模型在SIS模型的基础上，还考虑了病人被治愈后，可能会产生抗体，而不会被再次感染的情况，适应性更强。
SIR模型中，有三种人群：健康者（S），感染者（I），免疫者（R）

• 假设总人数为N，且N不变
• 假设时刻t健康人、感染者和免疫者所占比例分别为s(t)、i(t)和r(t)，且s(t)+i(t)+r(t)=1
• 假设每个病人每天有效接触人数为L（日接触率），感染者接触健康者，就会让健康者患病
• 假设病人每天的治愈率为M（日治愈率）
• 假设病人被治愈后，会产生抗体，成为免疫者，免疫者群体不会被再次感染
  

Matlab代码：

% 传染病SIR模型
% 清空工作区和变量区
clear;clc;
% 定义迭代次数
n = 100;
% 定义并初始化状态E(s,i,r)
E = zeros(3,n);
E(1,1) = 0.99; % 初始健康者比例
E(2,1) = 0.01; % 初始感染者比例
E(3,1) = 1 - E(1,1) - E(2,1); % 初始免疫者比例(假设一开始没有免疫者)
% 初始化参数
L = 0.5; % 病人日接触率
M = 0.1; % 日治愈率
% 开始迭代
for t = 1:n-1E(1,t+1) = E(1,t) - L*E(1,t)*E(2,t);E(2,t+1) = E(2,t) + L*E(1,t)*E(2,t) - M*E(2,t);E(3,t+1) = 1 - E(1,t+1) - E(2,t+1);
end
% 绘图
s = E(1,:); % 健康者比例数据
i = E(2,:); % 感染者比例数据
r = E(3,:); % 免疫者比例数据
plot(s,'DisplayName','s');hold on;
plot(i,'DisplayName','i');
plot(r,'DisplayName','r');
legend('健康者比例','感染者比例','免疫者比例');
xlabel('迭代次数');
ylabel('比例');
grid on;
hold off;

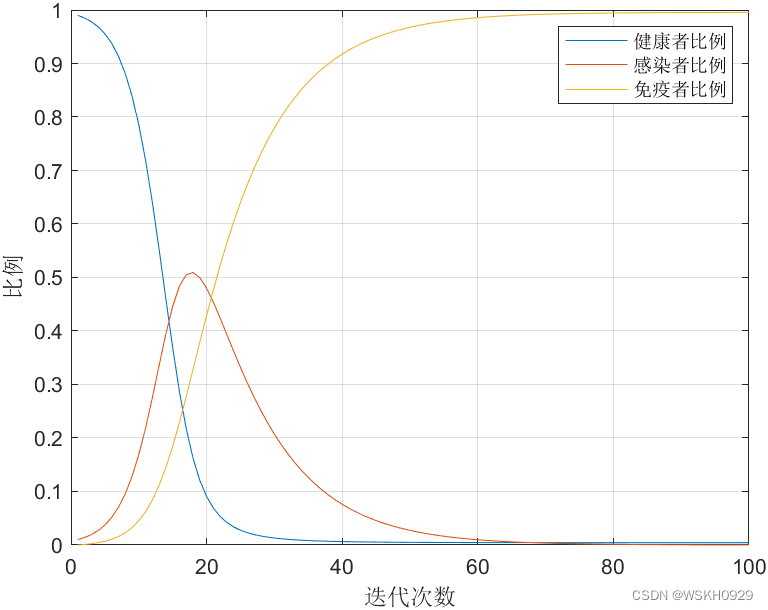
可以看到，在SIR模型中，随着时间的推移，感染者人数先上升，达到一个峰值后，再下降，最后下降为0，所有人都成为免疫者