Dijkstra最短路径算法
按路径长度的递增次序,逐步产生最短路径的贪心算法
基本思想:首先求出长度最短的一条最短路径,再参照它求出长度次短的一条最短路径,依次类推,直到从顶点v 到其它各顶点的最短路径全部求出为止。
时间复杂度为O(n2)
算法流程:

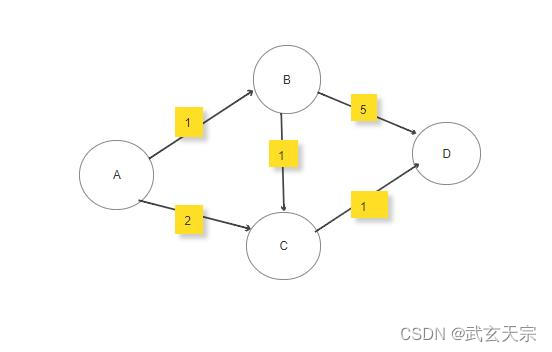
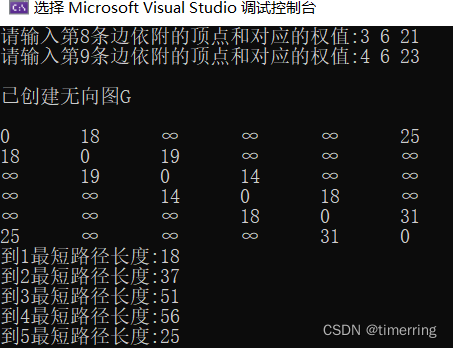
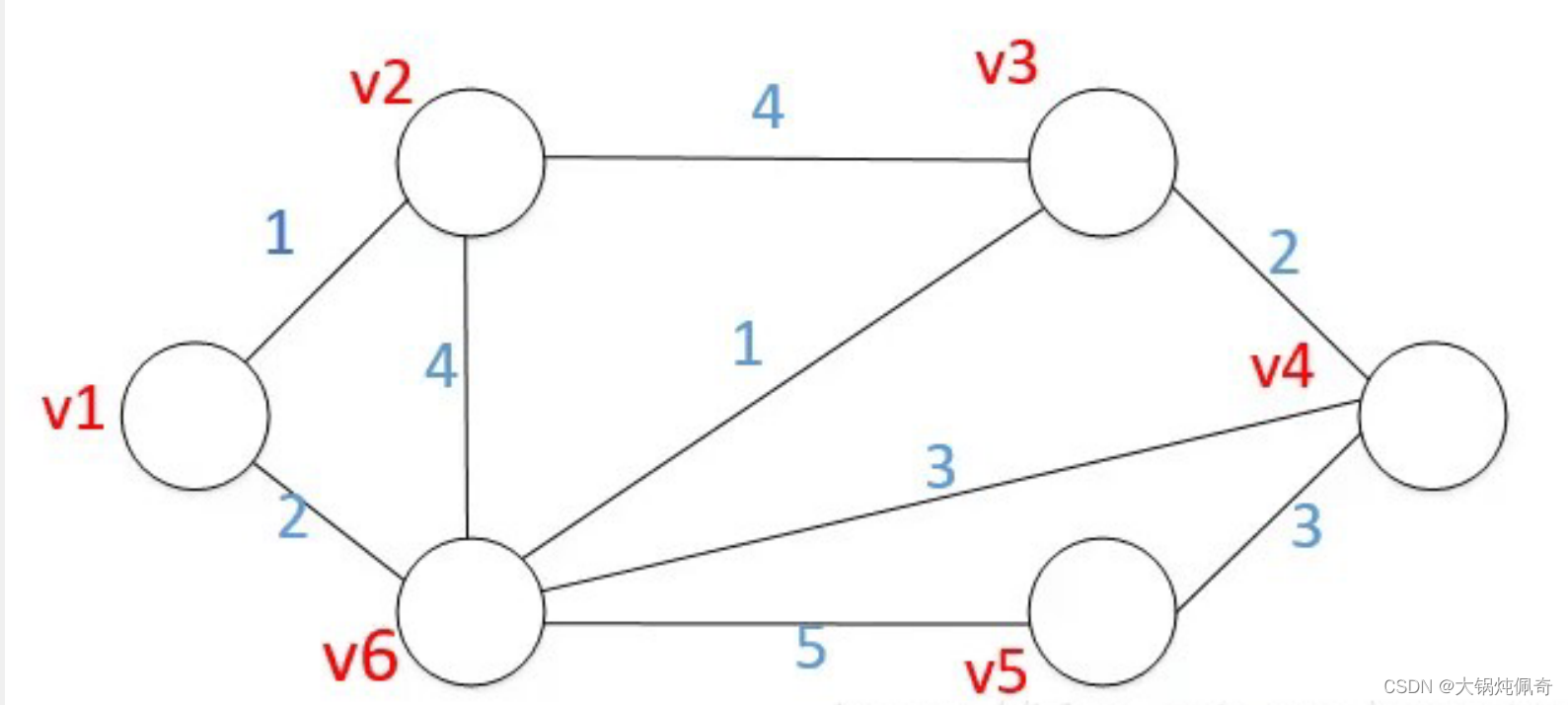
- 首先选定源点1,建立邻接矩阵C[5] [5],初始化三个数组分别为D[n],P[n],S[n],分别用来存储从源点到对应点的最短距离和最短路径上到该序列节点的前序节点,以及是否已经找到最短路径。
- 开始遍历源点的出边,将邻接矩阵的第一行放入数组D,找出距离最小的节点序号2,将数组P中的P[2]置为1,因为2的前序节点为1。
- 以上一步骤找到的节点为起点,继续遍历其邻接点(此处为2),若C[1][2]+C[2][m]<D[m] 则将其替换进数组D中,并将数组P中的P[m]置为2,因为m最短路径上的前序节点为2,节点2的邻接点全部遍历完成后,再从数组D中找出值最小且未被选中过的节点
- 重复以上步骤3,直到所有点都已经加入到数组S中。

程序实现:
public class Dijikstra extends Strategy {// open表Map<Integer, Node> open = new HashMap<>();// close表Map<Integer, Node> close = new HashMap<>();// 动作列表int[][] motion = get_motion();@Overridepublic List<Location> nextstep(Location start, Location work) {Node startnode = new Node(start.getX(), start.getY(), 0, -1);Node worknode = new Node(work.getX(), work.getY(), 0, -1);// 将起点放入open表open.put(cal_grid_index(startnode), startnode);// 向起点的上下左右四个方向扩展while (true) {// 与Astar算法不同 A*算法含有启发式函数 可以保证更快找到目标点// 但A*算法有可能永远无法找到目标点// Dijikstra算法虽然较慢 会遍历全部方向的点 但一定可以找到一条到目标点的路径// 找到map中节点cost最小的元素int temp_cost = Integer.MAX_VALUE;int current_id = 0;Node current = null;for (Map.Entry<Integer, Node> entry : open.entrySet()) {int current_cost =entry.getValue().cost + cal_Manhattan_distance(entry.getValue(), worknode);if (current_cost < temp_cost) {current_id = entry.getKey();temp_cost = current_cost;current = entry.getValue();}}// 判断是否找到目标点if (current.x == work.getX() && current.y == work.getY()) {System.out.println("找到目标点!");worknode.pind = current.pind;worknode.cost = current.cost;break;}// 移除open表中的current节点for (Iterator<Integer> iterator = open.keySet().iterator(); iterator.hasNext();) {Integer key = iterator.next();if (key == current_id) {iterator.remove();}}// 将current节点放入close表中close.put(current_id, current);for (int i = 0; i < motion.length; i++) {Node node = new Node(current.x + motion[i][0], current.y + motion[i][1],current.cost + motion[i][2], current_id);int node_id = cal_grid_index(node);// 该节点不能被扩展if (!verify_node(node)) {continue;}// 该节点已被确认过if (close.containsKey(node_id)) {continue;}// 将新扩展节点放入open表中if (!open.containsKey(node_id)) {open.put(node_id, node);} else {// 更新open表if (open.get(node_id).cost > node.cost) {open.put(node_id, node);}}}}open.clear();return cal_final_path(worknode, close);}/*** 根据终点回溯计算最短路径* * @param worknode* @param close* @return*/private List<Location> cal_final_path(Node worknode, Map<Integer, Node> close) {List<Location> ans = new ArrayList<>();int pind = worknode.pind;int i = 0;while (pind != -1) {// System.out.println(i);Node node = close.get(pind);Location location = new Location(node.x, node.y);ans.add(location);pind = node.pind;}return ans;}/*** 计算曼哈顿距离* * @param now* @param end* @return*/private int cal_Manhattan_distance(Node now, Node end) {return Math.abs(now.x - end.x) + Math.abs(now.y - end.y);}/*** 判断节点是否合理 1. 是否超出范围 2. 是否遇到货柜* * @param node* @return*/private boolean verify_node(Node node) {Container[][] map = ContainerMap.getMap();if (node.x < 0 || node.x >= ContainerMap.N || node.y < 0 || node.y >= ContainerMap.N) {return false;}if (map[node.x][node.y] != null) {return false;}return true;}/*** 计算栅格地图中的线性坐标* * @param node* @return*/private int cal_grid_index(Node node) {return node.y * ContainerMap.N + node.x;}/*** 定义动作及其代价 motion = {dx, dy, cost}* * @return*/private int[][] get_motion() {int[][] motion = {{1, 0, 1}, {0, 1, 1}, {-1, 0, 1}, {0, -1, 1}};return motion;}
}
A*算法
利用A*算法在拓扑地图上实现的路径规划:
关键:代价函数
- 对于任意节点n
• g(n)=从树根到n的代价
• h*(n)=从n到目标节点的优化路径的代价
• f*(n)=g(n) + h*(n)是节点n的代价 - 估计h*(n)
• 使用任何方法去估计h*(n), 用h(n)表示h*(n)的估计
• h(n) <= h*(n)总为真
• f(n)=g(n)+h(n) <= g(n)+h*(n)=f*(n)定义为n的代价
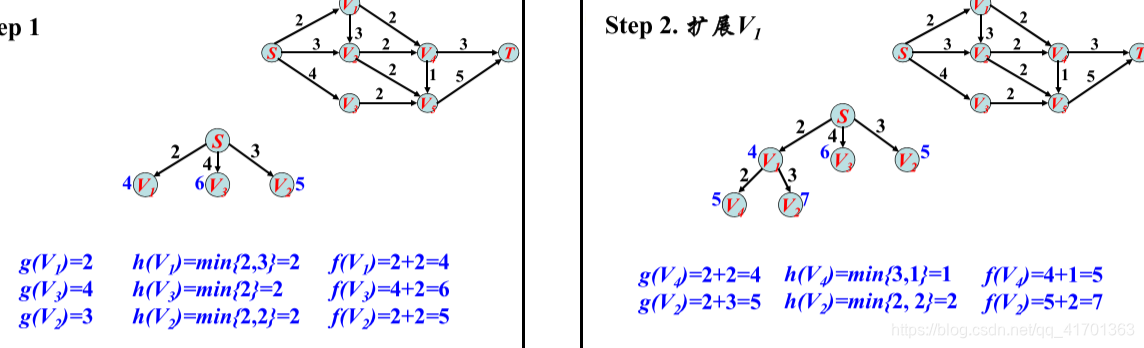
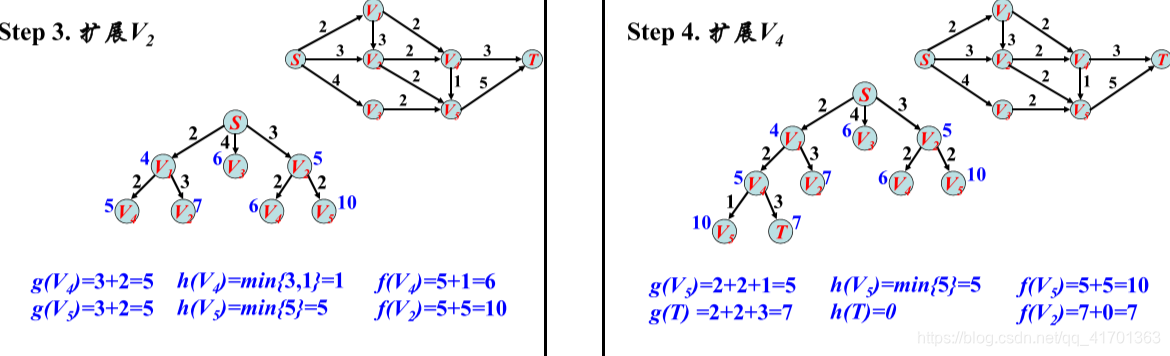
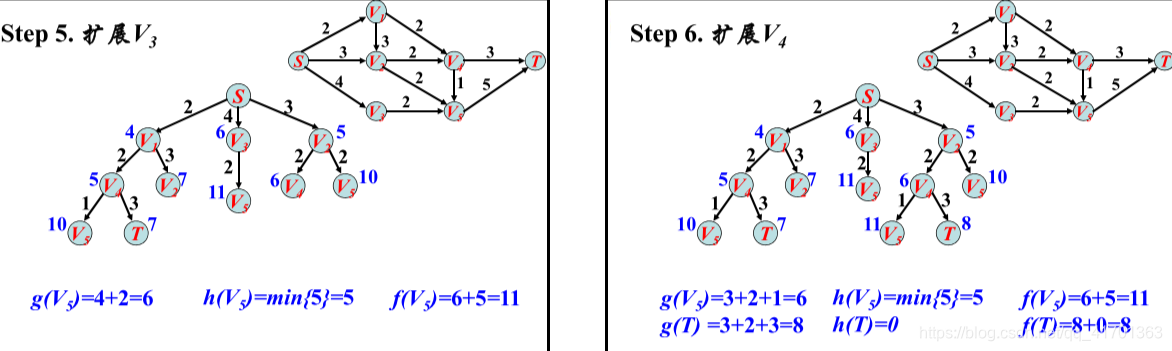
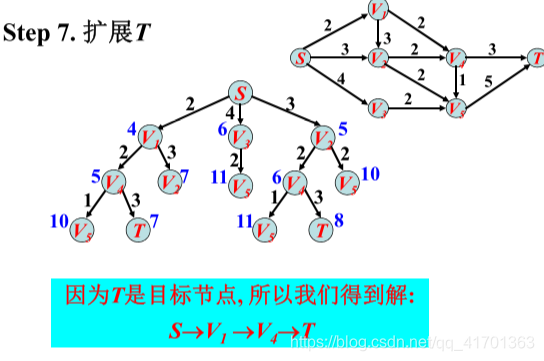
利用A*算法在栅格地图上实现的路径规划:
A*算法的核心思想是通过设置代价函数对未遍历点进行筛选,使搜索方向更偏向目标点,缩小搜索范围,进而提升搜索速度。公式f(n)=g(n)+h(n)是路径成本表达式。其中,f(n)为起点P—遍历中间点n—目标点g的路径总成本;g(n)为起点P—遍历中间点n之间的实际路径成本;h(n)为遍历中间点n—目标点Q的预估路径成本。寻找到最优解的条件是f(n)尽可能接近起点P到目标点Q的真实路径成本,此时搜寻到的点都是最短路径的过程点。由于遍历中间点n的g(n)值己知,因此只能提升h(n)的估计准确性,根据AGV在作业环境中只有“上下左右”四个行走方向,所以选取 h(n) = |Xn - XQ|+|Yn - YQ| (即曼哈顿距离),
算法流程描述如下:
(1)新建两个列表用作路径数据点存储:open list和close list,open list初始默认包含路径起点;
(2)计算与起点相邻的节点的f(n),按数值大小进行排序,f(n)最小的节点m转移到close list作为当前最优路径过程点,其余点留在open list中做备选点。
(3)若m为目标点,则停止搜索,并输出最优路径结果,否则继续;
(4)计算遍历中间栅格点m的所有相邻栅格点的f(n),若相邻节点n未加入open list,及时添加,并令g(n) = g(m) + d(m,n),此时n的父节点为m;若相邻点n在open list中,当g(n) > g(m) + d(m,n)时,更新g(n) = g(m) + d(m,n),设置n的父节点为m;
(5)遍历完所有备选点后重复步骤(2)-(4),直到目标点Q出现在open list中,搜索结束,按进入closed list的先后顺序输出中的节点栅格序列,该序列即为最优路径。
程序实现:
public class Astar extends Strategy {// open表Map<Integer, Node> open = new HashMap<>();// close表Map<Integer, Node> close = new HashMap<>();// 动作列表int[][] motion = get_motion();@Overridepublic List<Location> nextstep(Location start, Location work) {Node startnode = new Node(start.getX(), start.getY(), 0, -1);Node worknode = new Node(work.getX(), work.getY(), 0, -1);// 将起点放入open表open.put(cal_grid_index(startnode), startnode);// 向起点的上下左右四个方向扩展while (true) {if (open.size() == 0) {System.out.println("open表空!查找失败!");break;}// 找到map中节点cost最小的元素int temp_cost = Integer.MAX_VALUE;int current_id = 0;Node current = null;for (Map.Entry<Integer, Node> entry : open.entrySet()) {int current_cost =entry.getValue().cost + cal_Manhattan_distance(entry.getValue(), worknode);if (current_cost < temp_cost) {current_id = entry.getKey();temp_cost = current_cost;current = entry.getValue();}}// 判断是否找到目标点if (current.x == work.getX() && current.y == work.getY()) {System.out.println("找到目标点!");worknode.pind = current.pind;worknode.cost = current.cost;break;}// 移除open表中的current节点for (Iterator<Integer> iterator = open.keySet().iterator(); iterator.hasNext();) {Integer key = iterator.next();if (key == current_id) {iterator.remove();}}// 将current节点放入close表中close.put(current_id, current);for (int i = 0; i < motion.length; i++) {Node node = new Node(current.x + motion[i][0], current.y + motion[i][1],current.cost + motion[i][2], current_id);int node_id = cal_grid_index(node);// 该节点不能被扩展则查找下一个节点if (!verify_node(node)) {continue;}// 该节点已被确认过则查找下一个节点if (close.containsKey(node_id)) {continue;}// 将新扩展节点放入open表中if (!open.containsKey(node_id)) {open.put(node_id, node);} else {// 更新节点的代价if (open.get(node_id).cost > node.cost) {open.put(node_id, node);}}}}open.clear();return cal_final_path(worknode, close);}/*** 根据终点回溯计算最短路径* * @param worknode* @param close* @return*/private List<Location> cal_final_path(Node worknode, Map<Integer, Node> close) {List<Location> ans = new ArrayList<>();int pind = worknode.pind;int i = 0;while (pind != -1) {// System.out.println(i);Node node = close.get(pind);Location location = new Location(node.x, node.y);ans.add(location);pind = node.pind;}return ans;}/*** 计算曼哈顿距离* * @param now* @param end* @return*/private int cal_Manhattan_distance(Node now, Node end) {return Math.abs(now.x - end.x) + Math.abs(now.y - end.y);}/*** 判断节点是否合理 1. 是否超出范围 2. 是否遇到货柜* * @param node* @return*/private boolean verify_node(Node node) {Container[][] map = ContainerMap.getMap();if (node.x < 0 || node.x >= ContainerMap.N || node.y < 0 || node.y >= ContainerMap.N) {return false;}if (map[node.x][node.y] != null) {return false;}return true;}/*** 计算栅格地图中的线性坐标* * @param node* @return*/private int cal_grid_index(Node node) {return node.y * ContainerMap.N + node.x;}/*** 定义动作及其代价 motion = {dx, dy, cost}* * @return*/private int[][] get_motion() {int[][] motion = {{1, 0, 1}, {0, 1, 1}, {-1, 0, 1}, {0, -1, 1}};return motion;}
}