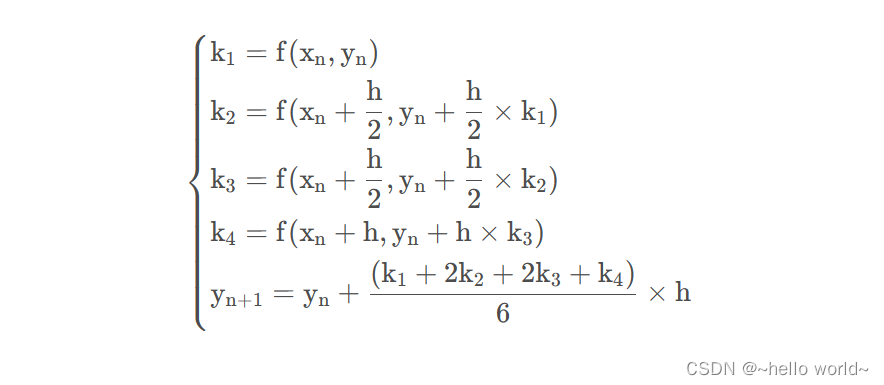1. 算法

上一篇介绍了显式欧拉法、隐式欧拉法、两步欧拉法和改进欧拉法求解常微分方程初值问题；其中显式欧拉法和隐式欧拉法是一阶算法精度，截断误差为$O\left(h^2\right)$；两步欧拉法和改进欧拉法是二阶算法精度，截断误差为$O\left(h^3\right)$；欧拉法的精度有限、需要求解步长$h$很小。本篇介绍求解精度更高的四阶龙格库塔法(Runge-Kutta)，其截断误差为$O\left(h^5\right)$。

对于一阶微分方程初值问题：

$\{\begin{array}{l}\dot{\mathbf{y}}=f\left(t,\mathbf{y}\right)\\ \mathbf{y}\left(t_0\right)={\mathbf{y}}_0\end{array}$

式中， $t_0$为初始时间（已知常数），${\mathbf{y}}_0$为初始状态（已知向量），$f\left(t,\mathbf{y}\right)$为关于时间$t$和状态$\mathbf{y}$的函数（已知函数）。

四阶龙格库塔法(Runge-Kutta)求解算法为：

$k_1=f\left(t\left(k\right),\mathbf{y}\left(k\right)\right)$
$k_2=f\left(t\left(k\right)+\frac{h}{2},\mathbf{y}\left(k\right)+\frac{h}{2}{k}_1\right)$
$k_3=f\left(t\left(k\right)+\frac{h}{2},\mathbf{y}\left(k\right)+\frac{h}{2}{k}_2\right)$
$k_4=f\left(t\left(k\right)+h,\mathbf{y}\left(k\right)+h{k}_3\right)$
$\mathbf{y}\left(k+1\right)=\mathbf{y}\left(k\right)+\frac{h}{6}\left(k_1+2k_2+2k_3+k_4\right)$
$\mathbf{y}\left(0\right)={\mathbf{y}}_0$

上式是关于$\mathbf{y}\left(k\right)$向$\mathbf{y}\left(k+1\right)$的递推形式，可以根据初始条件按照递推关系依次求出$\mathbf{y}\left(1\right),\mathbf{y}\left(2\right),\mathbf{y}\left(3\right),\mathbf{y}\left(4\right)\cdots ,\mathbf{y}\left(N\right)\cdots$，此离散序列即为微分方程的数值解。

微分方程的数值解法，本质是使用数值积分来实现$\dot{\mathbf{y}}$向$\mathbf{y}$的转换。四阶龙格库塔法通过对微分的四步分段逼近，在一个求解步长内能够逼近复杂的曲线，因此能够取得较高的计算精度，其截断误差为$O\left(h^5\right)$。

2. 程序

作者使用Matlab开发了四阶龙格库塔法求解常微分方程的程序，能够方便快捷的求解一阶常微分方程的初值问题。

function [T,X,dX] = ODE_RK4( Hfun,t,h,x0 )
% [T,X] = ODE_RK4( Hfun,t,h,x0 ) 4阶龙格-库塔法求解常微分方程
% Hfun为描述状态导数的函数句柄，格式为 dX = Hfun( t,X )
% 必须保证返回dX的格式为行向量
% t为时间节点，可为标量，时间范围为 T = 0:h:t
%             长2向量 ，时间范围为 T = t(1):h:t(2)
%             向量 ，时间范围为 T = t
% h为时间步长，在t的前两种情况下，必须给出h具体值
% 直接给出时间节点t时，h可用[]或任意值占位
% x0为状态量初始值  
% 算法：
%      K1  = Hfun( t(k-1),X(k-1) ) =  dX(k-1)
%      K2 =  Hfun( t(k-1)+h/2,X(k-1)+h*K1/2 )
%      K3 =  Hfun( t(k-1)+h/2,X(k-1)+h*K2/2 )
%      K4 =  Hfun( t(k-1)+h  ,X(k-1)+h*K3 )
%    X(k) =  X(k-1) + (h/6) * (K1 + 2*K2 + 2*K3 +K4)
% By ZFS@wust  2021
% 获取更多Matlab/Simulink原创资料和程序，清关注微信公众号：Matlab Fans

下面结合实例进行演示和分析。

3. 案例

求解一阶常微分方程（式中向量$\mathbf{x}$等价于前文中的向量$\mathbf{y}$）：
$\dot{\mathbf{x}}=f\left(t,\mathbf{x}\right)=\left[\begin{array}{c}\mathbf{x}(2)\ast \mathbf{x}(3)\\ -\mathbf{x}(1)\ast \mathbf{x}(3)\\ -0.51\ast \mathbf{x}(1)\ast \mathbf{x}(2)\end{array}\right]$
$\mathbf{x}\left(0\right)=\left[\begin{array}{c}0\\ 1\\ 1\end{array}\right]$

% 四阶龙格库塔算法(Runge-Kutta)测试程序
% By ZFS@wust  2021
% 获取更多Matlab/Simulink原创资料和程序，清关注微信公众号：Matlab Fansclear
clc
close all%%  仿真步长 h=0.6 时
Hfun = @(t,x) [ x(2)*x(3); -x(1)*x(3); -0.51*x(1)*x(2)];   % 一阶微分方程导数表达式% 参数
t = [0 12];     % 时间范围
h = 0.6;       % 时间步长
x0 = [0 1 1];   % 初始状态% 改进欧拉法求解
[T1,X1] = ODE_ImprovedEuler( Hfun,t,h,x0 );
% 改进欧拉法求解
[T2,X2] = ODE_RK4( Hfun,t,h,x0 );
% Matlab自带ode45求解
[T3,X3] = ode45( Hfun,t(1):h:t(2),x0 );% 绘图对比
figure
subplot(311)
plot(T1,X1(:,1),T2,X2(:,1),T3,X3(:,1))
xlabel('Time(s)')
ylabel('x_1')
legend('改进欧拉法','四阶龙格库塔法','ode45')
subplot(312)
plot(T1,X1(:,1),T2,X2(:,1),T3,X3(:,1))
xlabel('Time(s)')
ylabel('x_2')
legend('改进欧拉法','四阶龙格库塔法','ode45')
subplot(313)
plot(T1,X1(:,1),T2,X2(:,1),T3,X3(:,1))
xlabel('Time(s)')
ylabel('x_3')
legend('改进欧拉法','四阶龙格库塔法','ode45')%%  仿真步长 h=0.9 时
% 参数
h = 0.9;       % 时间步长% 改进欧拉法求解
[T1,X1] = ODE_ImprovedEuler( Hfun,t,h,x0 );
% 改进欧拉法求解
[T2,X2] = ODE_RK4( Hfun,t,h,x0 );
% Matlab自带ode45求解
[T3,X3] = ode45( Hfun,t(1):h:t(2),x0 );% 绘图对比
figure
subplot(311)
plot(T1,X1(:,1),T2,X2(:,1),T3,X3(:,1))
xlabel('Time(s)')
ylabel('x_1')
legend('改进欧拉法','四阶龙格库塔法','ode45')
subplot(312)
plot(T1,X1(:,1),T2,X2(:,1),T3,X3(:,1))
xlabel('Time(s)')
ylabel('x_2')
legend('改进欧拉法','四阶龙格库塔法','ode45')
subplot(313)
plot(T1,X1(:,1),T2,X2(:,1),T3,X3(:,1))
xlabel('Time(s)')
ylabel('x_3')
legend('改进欧拉法','四阶龙格库塔法','ode45')

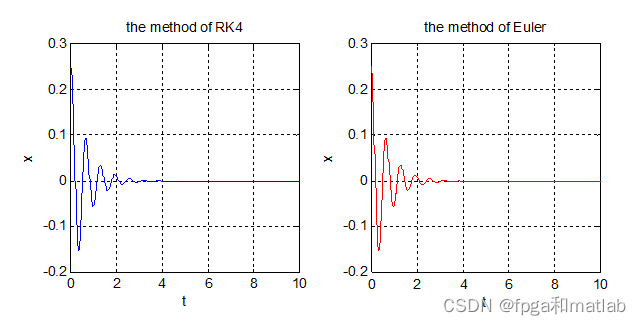
不同时间步长$h$时的数值计算结果：

• 步长$h=0.6s$
  

• 步长$h=0.9s$
  

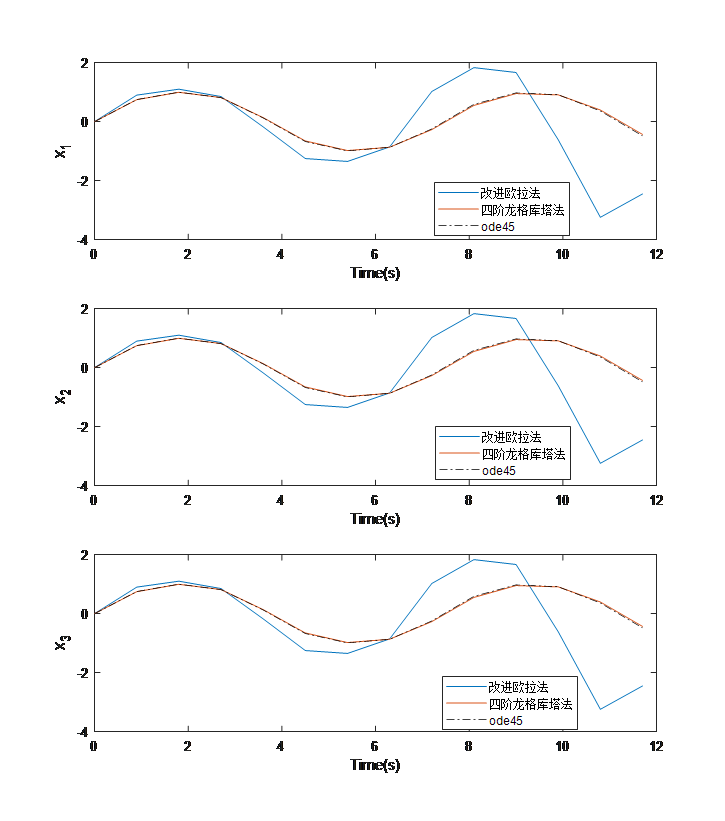
从计算结果可以看出，四阶龙格库塔法(Runge-Kutta)即使在步长很大时，也能保持较高的求解精度，求解精度与Matlab自带的ode45函数相当，相对于改进欧拉算法求解精度有明显提高。
自己编程实现四阶龙格库塔法(Runge-Kutta)，相对于直接调用ode45等Matlab自带的龙格库塔法的最大优势在于：可以将求解程序和模型描述文件融合起来，解决各类参数时变、条件判断、多模型切换等问题。后续补充实际案例。

4. 联系作者

有Matlab/Simulink方面的技术问题，欢迎发送邮件至944077462@qq.com讨论。
更多Matlab/Simulink原创资料，欢迎关注微信公众号：Matlab Fans

源程序下载:
1. csdn资源: 四阶龙格库塔法(Runge-Kutta)求解常微分方程的Matlab程序及案例
2. 扫码关注微信公众号Matlab Fans，回复BK09获取百度网盘下载链接。