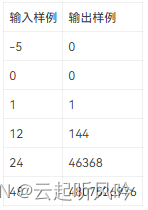
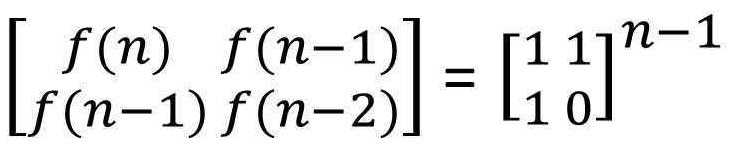龙格-库塔(Runge-Kutta)方法C++实现

article/2025/8/29 22:23:23

龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。由于此算法精度高，采取措施对误差进行抑制，所以其实现原理也较复杂。该算法是构建在数学支持的基础之上的。

1 中点法

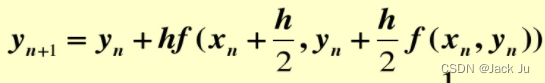
在这里插入图片描述

2传统二阶龙格库塔法：

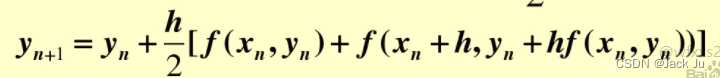
在这里插入图片描述

3 传统三阶龙格库塔法

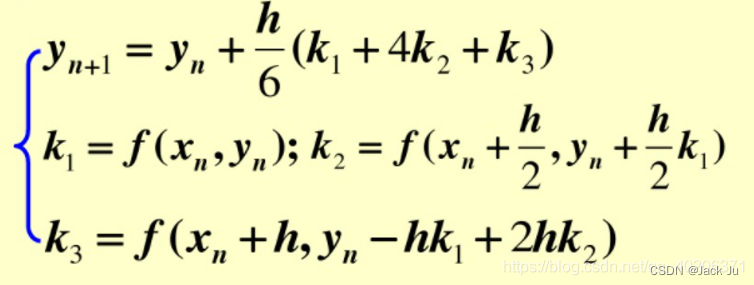
在这里插入图片描述

4 传统四阶龙格库塔法

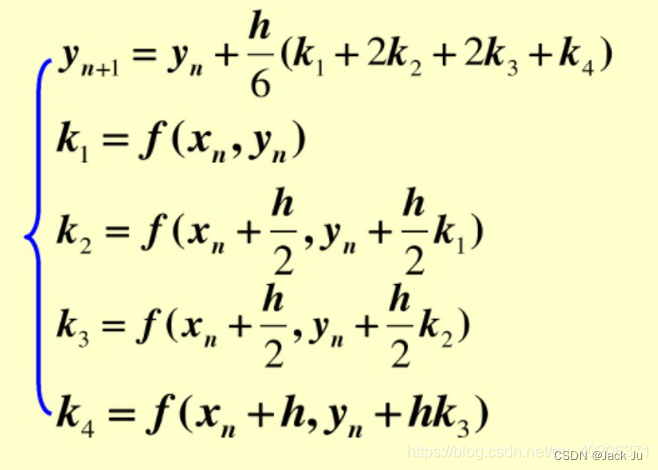
在这里插入图片描述

5四阶龙格库塔法举例

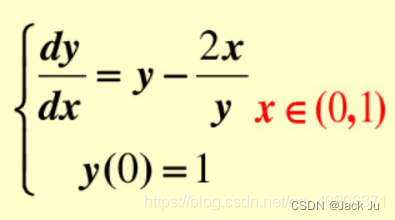
在这里插入图片描述

我们使用经典四阶龙格库塔法：

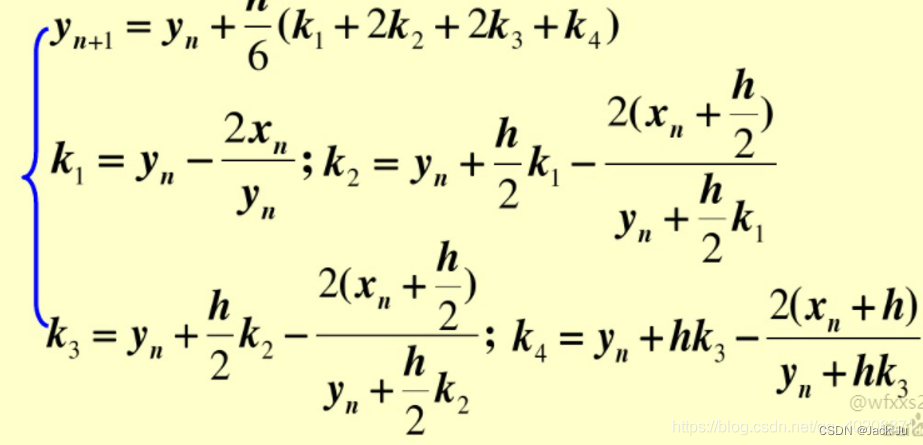
在这里插入图片描述

6 C++

这里主要使用的是经典四阶龙格库塔法，重写如下：

方程的导数和初值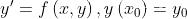： $y'=f\left ( x, y \right ), y\left ( x_{0} \right )=y_{0}$

方程的迭代计算公式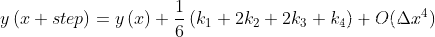： $y\left ( x+step \right )=y\left ( x \right )+\frac{1}{6}\left ( k_{1}+2k_{2}+2k_{3}+k_{4} \right )+O(\Delta x^{4})$

其中，
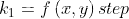
$k_{1}=f\left ( x, y \right )step$
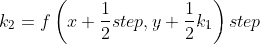
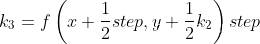
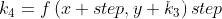
在这里插入图片描述

在这里插入图片描述
根据其原理以及例子：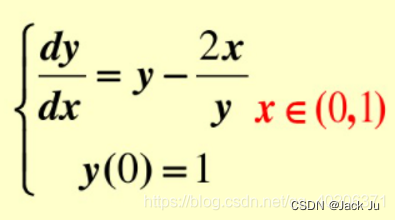

C++代码如下：

#include <iostream>
#include <fstream>
#define Count 100 //Number of calculations
//#define ITEM 0.001 //Calculation accuracy
class Longkuta
{
public :std::fstream fileopen;  Longkuta(double initx,double inity ,double inith ); // Initial calculation point step size//~Longkuta();void progess( );bool write();double fun(double x0,double y0);   //Define function heredouble  x0 , y0, h  ;
};Longkuta::Longkuta(double initx,double inity ,double inith )
{x0=initx;y0=inity;h=inith;
}bool Longkuta::write( )
{fileopen.open("data.txt",std::ios::app);if (fileopen.is_open()){return true;}else{std::cout<<"File open failed\n";return false;}
}
void Longkuta::progess( )
{int i = 1;double K1,K2,K3,K4,y1,x1;while ( i<Count){x1 = x0+h;K1=fun(x0,y0);K2=fun(x0+h/2,y0+K1*h/2);K3=fun(x0+h/2,y0+K2*h/2);K4=fun(x1,y0+h*K3);y1=y0+h*(K1+2*K2+2*K3+K4)/6.0;fileopen<<"Calculations"<<i<<"  " <<"x= "<<x1<<" y = "<<y1<<"\n";x0=x1;y0=y1;i++;//if ((y0-y1)>ITEM)//	break;}fileopen.close();std::cout<<"The calculation result is"<<y0;
}double Longkuta::fun(double x0 ,double y0)  //Function expression
{double dy;dy = y0-(2*x0)/y0;return dy;
}int main()
{Longkuta longkuta(0,1,0.05);if (longkuta.write()){longkuta.progess();}elsestd::cout<<"Failed to write data"<<std::endl;return 0;
}