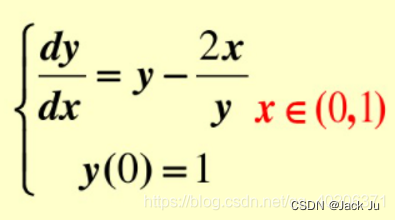1、龙格-库塔法简介

   龙格—库塔法是一种在工程上应用广泛的高精度单步算法，其中包括著名的欧拉法，用于数值求解微分方程。 由于此算法精度高，采取措施对误差进行抑制，所以其实现原理也较复杂。 在各种龙格—库塔法当中有一个方法十分常用，该方法主要是在已知方程导数和初值信息，利用计算机仿真时应用，省去求解微分方程的复杂过程，该方法被称为“RK4”或者就是“龙格—库塔法”。

2、龙格-库塔法基本思想

   在了解龙格—库塔法之前先回顾一下欧拉法。

2.1 欧拉法基本原理

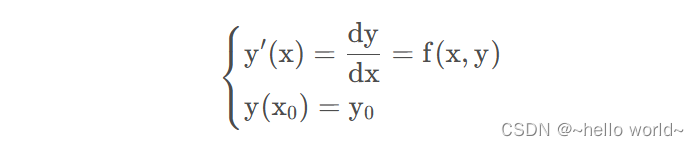
   若已知上述方程组某点坐标，以及该点的斜率值，则可以使用欧拉法对 y(x) 进行迭代的近似求解。求解分析：已知 x = x₀ 时 y = y₀ y=y ，且斜率为 y′( x₀) = f ( x₀ , y₀ ) ，那么就可以用过该点且斜率为 y′( x₀) 的直线近似求解 x₀ 附近一点 x₁ 的函数值。

   构建直线：

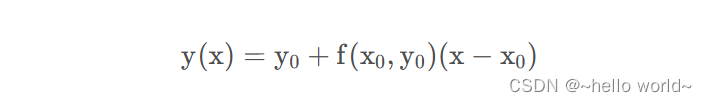
   那么，在 x = x₁ 时，求得：

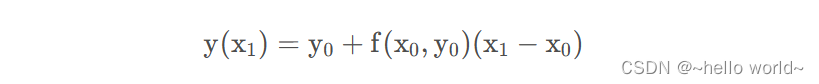
可以求得 y = y ( x₁ )，重复以上步骤，可以求得 y(x₂) , y(x₃) , ⋯   , y (x_n) 。如果等间隔取 x 值，即 x₁−x₀= x₂− x₁ = x₃ − x₂ = ⋯ = x_n − x_n−1 = h，也即 x_n = x₀ + n ⋅ h 可以得到

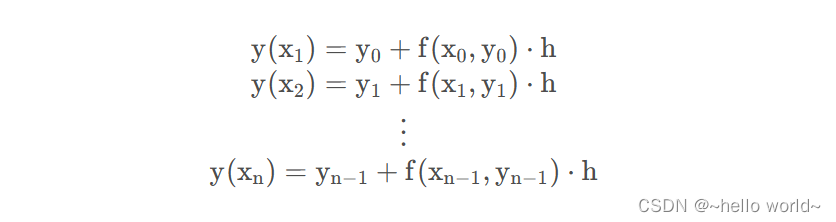
总结为：

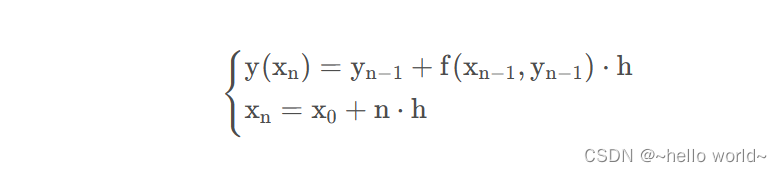
该公式就是欧拉公式。

2.2 龙格-库塔基本原理

   龙格-库塔算法是对欧拉法的改进，都是使用过 ( x_k , y_k) 的直线来近似下一点的函数值 y_k+1 ，区别在于斜率的选择。在欧拉法中，直接使用该点的切线 y′(x_k) 当做直线的斜率，这样会造成对于 y(x_k+1) 的求解一定存在误差，除非 y(x) 为直线时，结果才是准确的。基于上面的考虑，需要解决的便是如何提高 y(x_k+1) 求解的精度；或者说在知道 ( x_k , y_k) 的情况下，如何确定直线斜率确保恰好经过待估测点 y(x_k+1) 。答案是利用拉格朗日中值定理。

   拉格朗日中值定理如下：

即在 ( x_k , x_k+1) 区间内存在一点 ϵ (x_k< ϵ < x_k+1) ，使得等式 f (x_k+1) − f (x_k) = f ′( ϵ ) (x_k+1 − x_k) 成立。

所以准确的直线方程为：

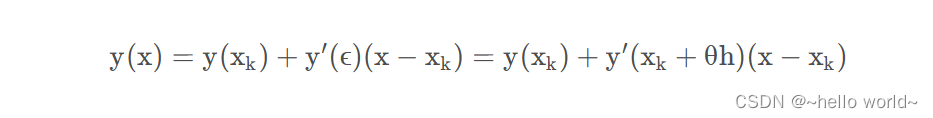
如果等间距取值，即 x_k+1 − x_k = h ，则有

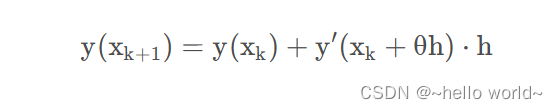
其中，θ ∈ ( 0 , 1 ) ，而当 θ = 0 时就是欧拉法。

.
   现在，原理已经明确了，但如何确定 y′(ϵ) 的取值？这就涉及到算法的精度问题。考虑到直接使用端点处 y′( x_k ) 的斜率不准确，那么取两端点斜率的平均准确度肯定就提升了一点，即y′(ϵ) 取

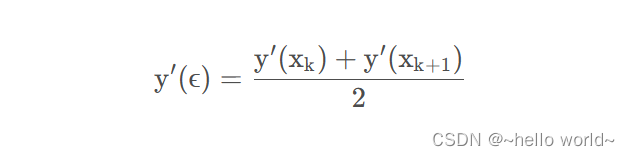
为了方便书写，将 y′(x_k) = κ₁， y′(x_k+1) = κ₂ ，即用 κ 表示斜率。则上式这可改写为：
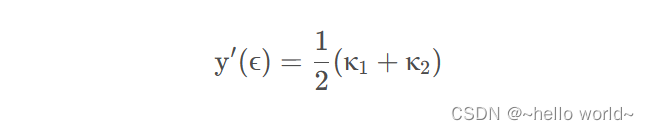根据已知条件方程 y′(x) = f(x,y) ，同理可得：

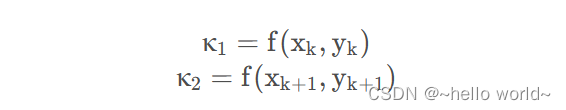
其中 f(x,y) 是已知的，而 f(x_k+1 , y_k+1) 中的 y_k+1 是未知的，若用欧拉法来估计此处的 y_k+1，即有：

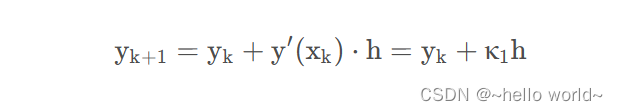
当然这是不准确的，若用两点的平均斜率来提高精，则有：

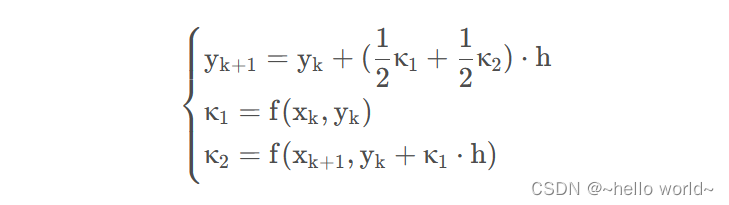
   值得注意的是，对于两端点斜率取平均是出于习惯，但实际应用中是对两斜率进行加权，取平均只是习惯性的把两者权重取相等而已，因此更一般描述为：

.
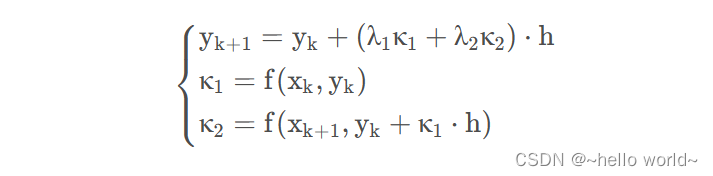
   根据上述斜率取平均值的思路，进行递推取 n 个点，获得更多点加权来估算 f′(ϵ) 的值所得结果精度肯定更高。现在，假设在 (x_k, x_k+1) 区间取 n 个点，对应点为 x_k+α₁h , x_k+α₂h , x_k+α₃h , ⋯   , x_k+α_nh , 且 α ∈ [ 0 , 1 ] ，在每个点的斜率记为 κ₁, κ₂, ⋯   , κ_n ，对应加权为 λ₁ , λ₂, ⋯   , λ_n ， 那么有

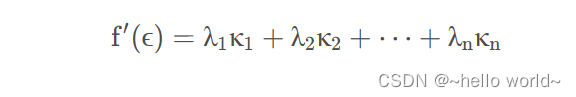
则有：

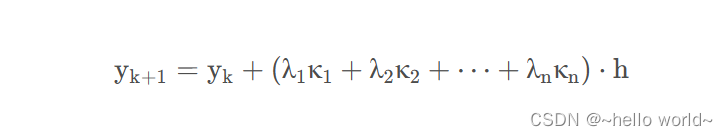
λ 为自取值，对于 κ 有：

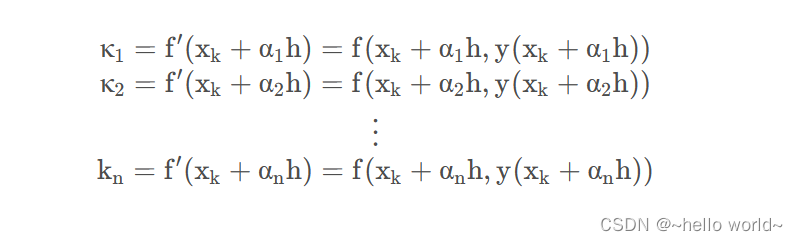
通常 α₁ 取0，即对应 x_k 点；此时，κ₁ = f (x_k, y_k) 。同样，对于其余式子 f 自变量中的 y(x_k+ α_nh ) 使用欧拉法来求，即有：

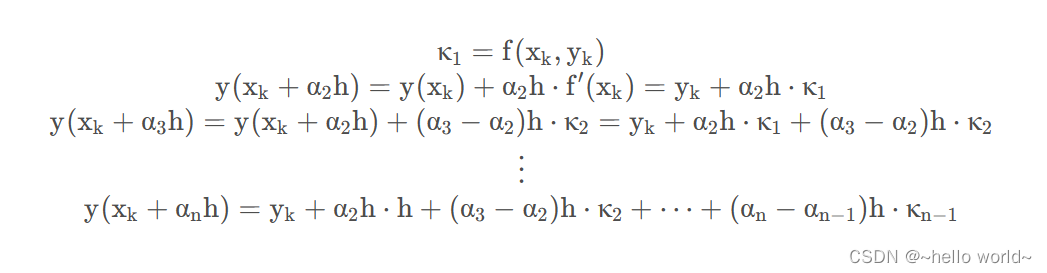
总结以上，即得到龙格-库塔基本表达式：

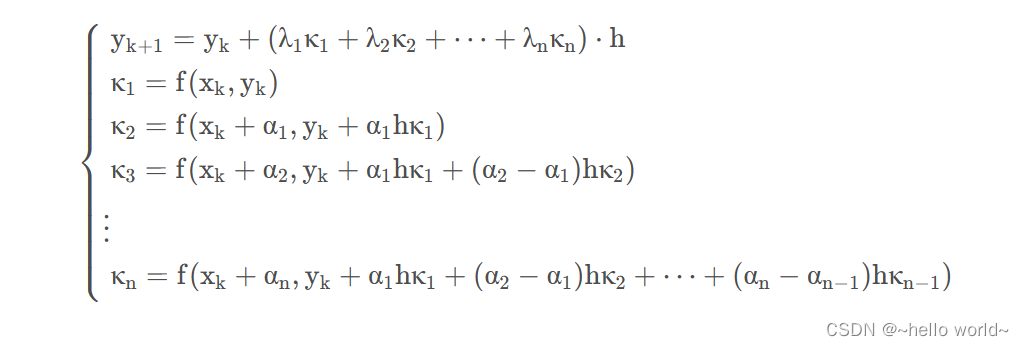
其中：λ₁, λ₂, ⋯ , λ_n 为对应采样点斜率权值，满足 λ₁ + λ₂ + ⋯ + λ_n = 1 ；

   α₁, α₂, ⋯ , α_n 为采样点位置比率，满足 0 < α₁ < α₂ < ⋯ < α_n

.

3、 案例：四阶龙格-库塔法求解微分方程

   本次案例使用的微分方程如下：

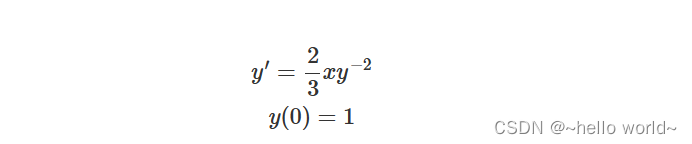
   本次案例使用的是常用的 经典R-K方法，如下：

.
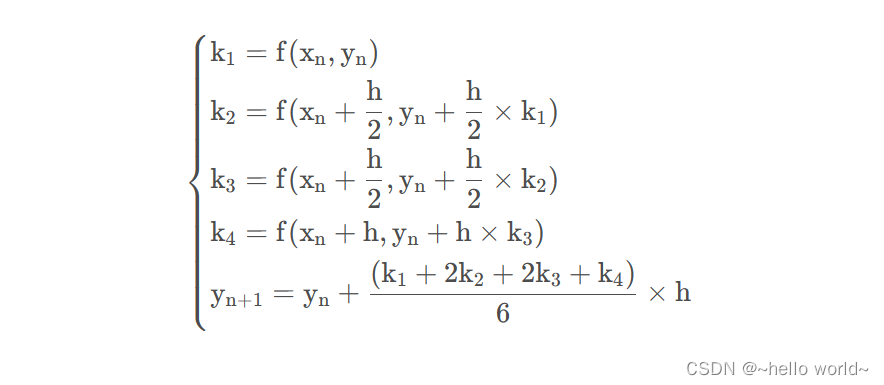
运行代码

# lgkt
import numpy as npdef RK(x0, y0, h, n, func):"""x0: 初始点x坐标y0: 初始点y坐标h: 步长n: 迭代次数func: 事先定义好的f(x,y)"""x = np.linspace(x0, x0 + (n - 1) * h, num=n)y = np.zeros_like(x)y[0] = y0for i in range(n - 1):k1 = func(x[i], y[i])k2 = func(x[i] + h / 2, y[i] + h * k1 / 2)k3 = func(x[i] + h / 2, y[i] + h * k2 / 2)k4 = func(x[i] + h, y[i] + h * k3)y[i + 1] = y[i] + h * (k1 + 2 * k2 + 2 * k3 + k4) / 6return x, yif __name__ == '__main__':# y'=f(x,y)=2x/(3y^2)f = lambda x, y: 2 * x / (3 * y * y)X, Y = RK(0, 1, h=0.4, n=5, func=f)print("X=", X)print("Y=", Y)