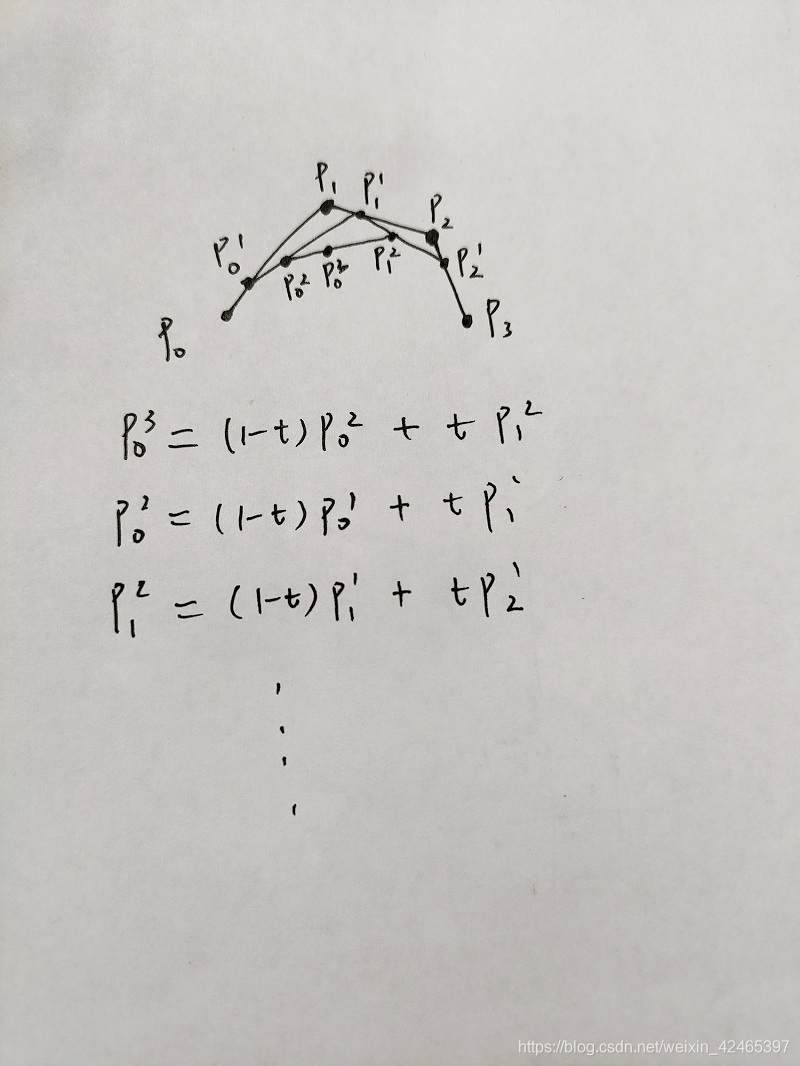Bezier曲线快速相交计算
- 背景介绍
- 算法思路
- 解释和分析
- 示例
- 参考资料
背景介绍
很多时候,需要计算曲线段与曲线段是否有交点。常规的思路是直接联立方程求解。不过,直接求方程的解这种思路通常在计算上开销较大。
针对任意曲线,曲线的方程阶次可能较高,无论是求导还是求根都比较困难。当曲线无交点时,并不能快速判断并停止计算。因此,本文介绍一种快速计算贝塞尔(Bezier)曲线的方法。这个方法的中心思想是化曲为直,分段判断。通过快速排除条件,可以节省计算时间。
算法思路
具体针对两条曲线(2D平面)进行说明:
1)采用AABB模型(Aixe Align Bounding Box)构建每条曲线的包围盒,对构建好的包围盒进行干涉判断,若空间干涉,进行下一步,否者退出本次判断;
2)对干涉空间内的曲线进行二分,即分成2段,2条曲线则分成四段。针对两两进行检测,执行步骤 1) ;
3)退出条件:曲线线段小于某一阈值或到达其他检测精度。
以上就是全部的思路,针对具体工程问题可以针对优化,进行加速计算。
解释和分析
不相交的曲线,在形成包围盒进行相交测试中可能会由于包围盒的范围太大而出现干涉,因此需要进一步二分,减少空间大小以排除或者确定。相交的曲线在该段内形成的包围盒一定会干涉,因此只需要收缩包围盒大小(也即曲线段范围缩小),就能找到交点(当然是一个近似结果,但一般能满足工程需要)。
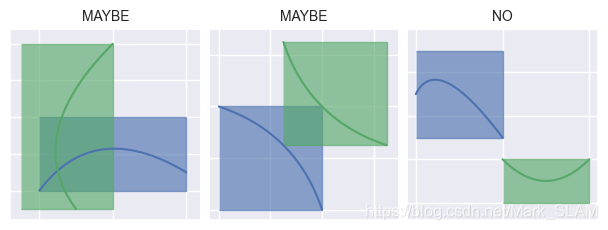
为什么要用AABB模型而不是OBB(Oriented Bounding Box)?
当然从实际角度考虑,曲线是有方向和走向的,使用OBB模型更符合实际。但是OBB的计算比较复杂,需要计算切线方向,涉及到求导等。另外OBB的干涉检测也比较复杂,需要用到分离轴SAT或者GJK算法进行判断,这无疑加大了计算量,每一步的OBB干涉判断耗时太大了。当然,不在乎实时性的可以采用该方法,进一步也可以采用基于OBB的紧包围盒(都不在乎计算量了,直接精确求解它不香嘛)。
AABB包围盒如何计算,如何判断干涉?
如果曲线的x,y从起点出发到终点,x及y的变化呈现递增or递减的情况,则可以简单处理。此时AABB可以由该曲线的两个点确定(起点和终点,其中一个是最大点,一个是最小点)。
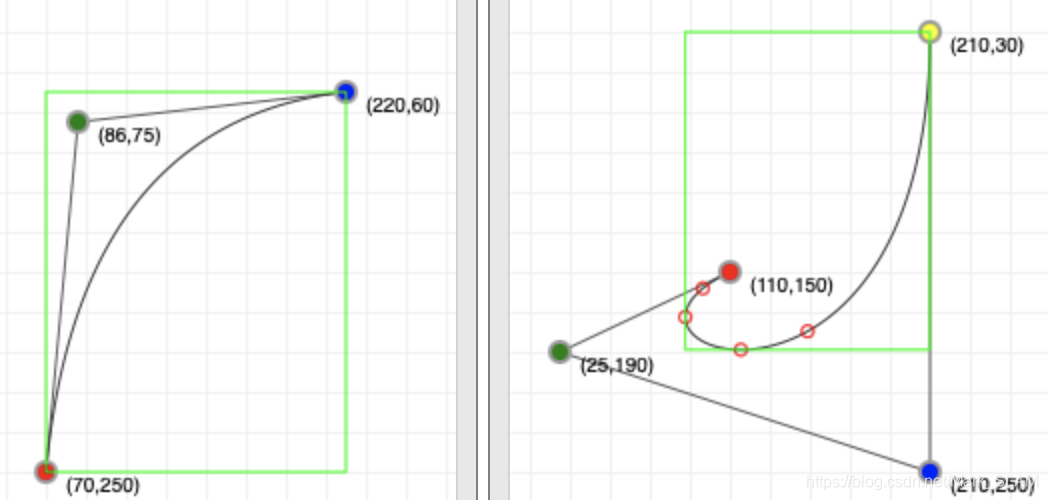
左边这个包围盒就只需要起点(70,250)和终点(220,60)就能确定了。右边这个则需要计算单调性改变处的坐标,并与起点和终点比较,最终构成AABB。具体确定单调性的方法,可以采用计算曲线导数(贝塞尔曲线的一阶导数为低一阶贝塞尔曲线),根据它确定根。
AABB的干涉判断比较简单了,x,y最大最小值直接判断就行了,可以参考其他教程。
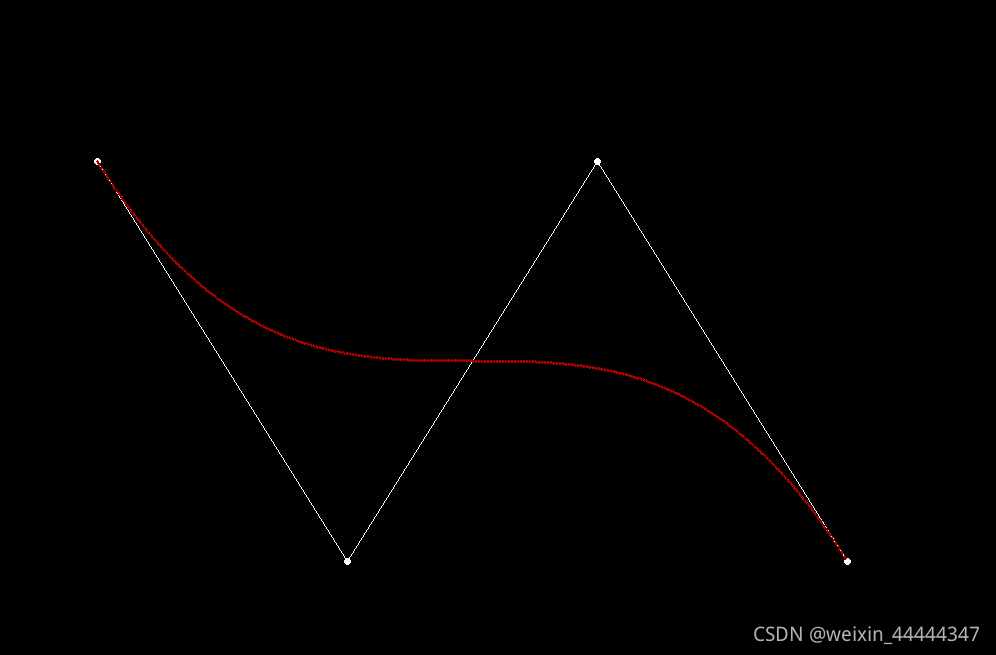
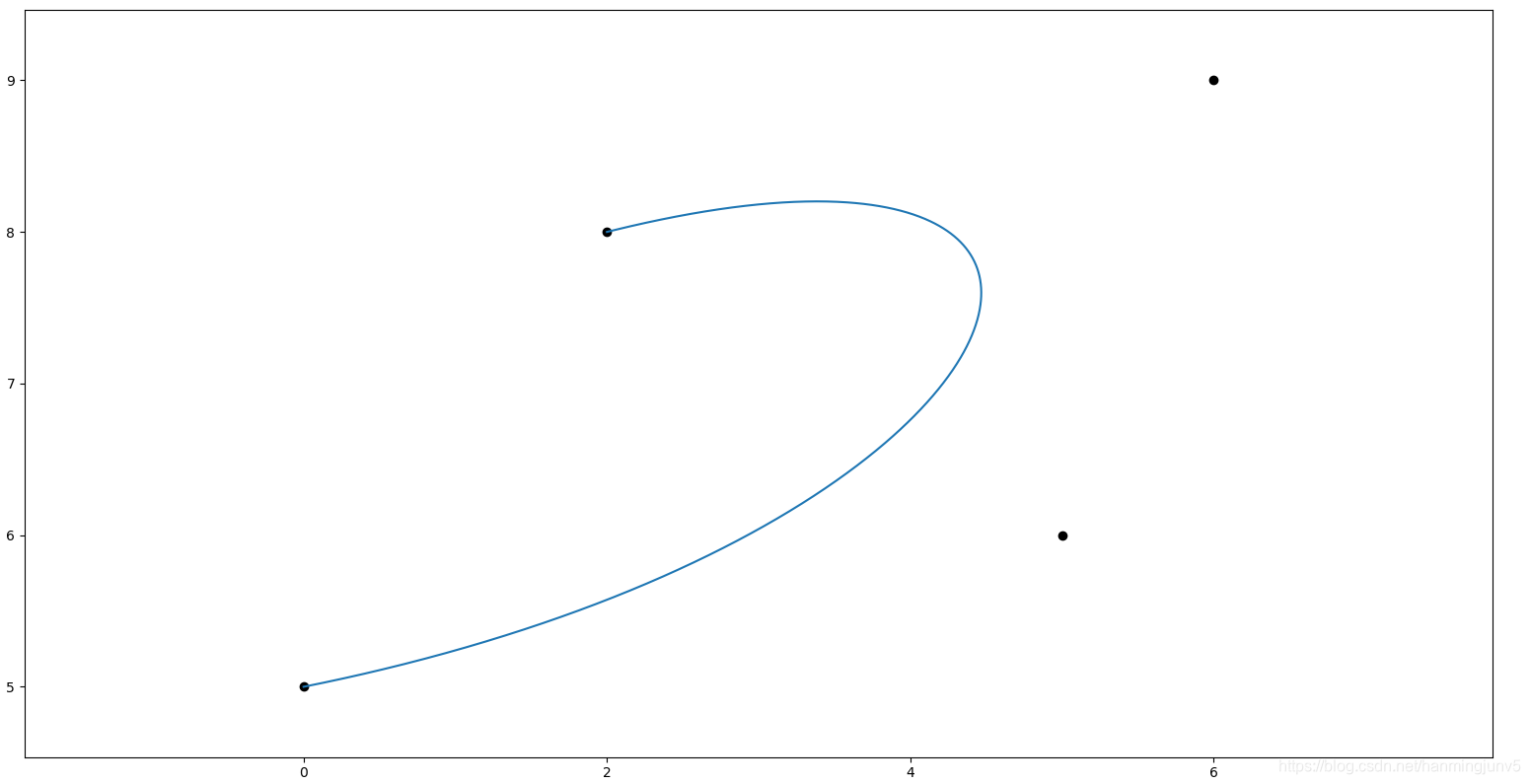
以下两张图是搜索过程展示(资源来自于链接)
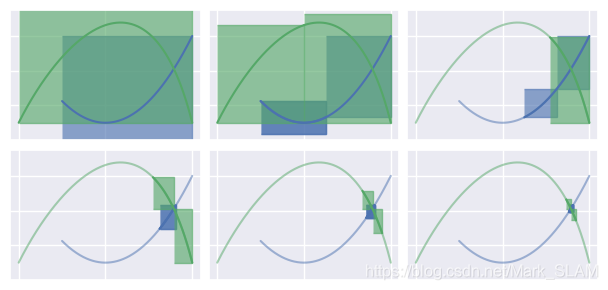
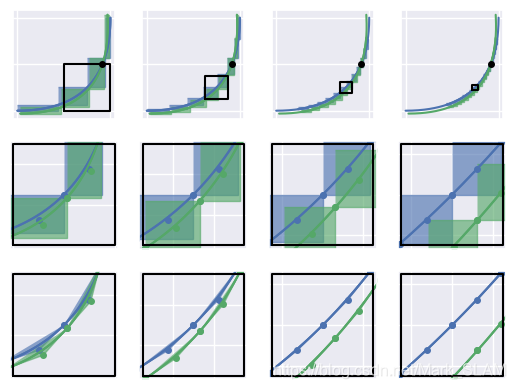
示例
此代码片段来自于python-bezier包
>>> import bezier
>>> import numpy as np
>>> nodes1 = np.asfortranarray([
... [0.0, 0.5, 1.0],
... [0.0, 1.0, 0.0],
... ])
>>> curve1 = bezier.Curve(nodes1, degree=2)
>>> nodes2 = np.asfortranarray([
... [0.0, 0.25, 0.5, 0.75, 1.0],
... [0.0, 2.0 , -2.0, 2.0 , 0.0],
... ])
>>> curve2 = bezier.Curve.from_nodes(nodes2)
>>> intersections = curve1.intersect(curve2)
>>> intersections
array([[0.31101776, 0.68898224, 0. , 1. ],[0.31101776, 0.68898224, 0. , 1. ]])
>>> s_vals = np.asfortranarray(intersections[0, :])
>>> points = curve1.evaluate_multi(s_vals)
>>> points
array([[0.31101776, 0.68898224, 0. , 1. ],[0.42857143, 0.42857143, 0. , 0. ]])
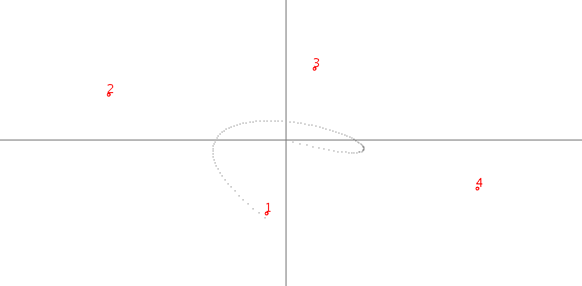
下图四个交点的位置,t1=0.31101776, 0.68898224, 0. , 1,对应t2=0.42857143, 0.42857143, 0. , 0.
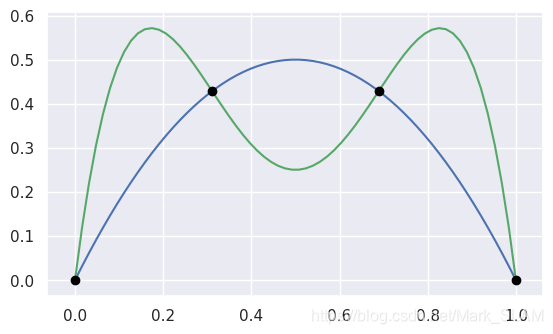
此方法的优点在于不需要计算导数及根,可以快速排除离得较远的曲线段。
参考资料
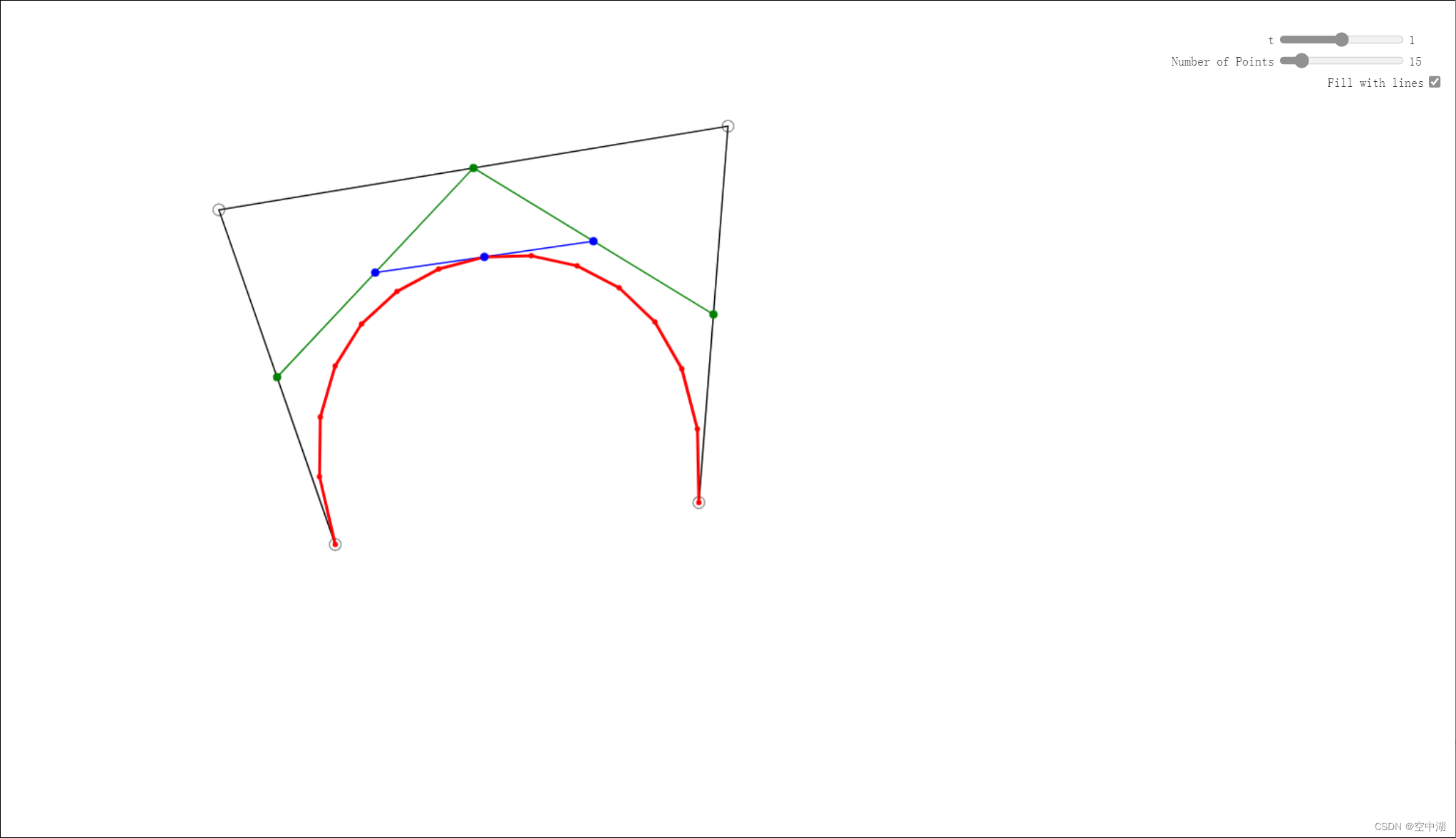
贝塞尔曲线的介绍:https://pomax.github.io/bezierinfo/
python代码:https://github.com/dhermes/bezier
欢迎留言交流,如果觉得有帮助,点个赞呗。