二分图最大匹配
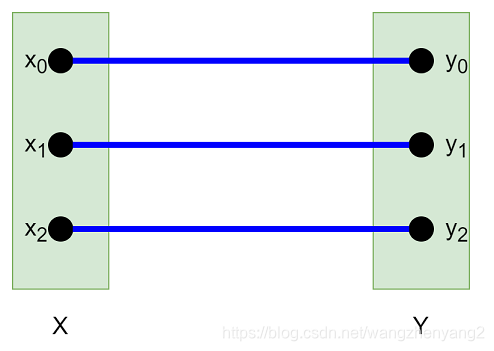
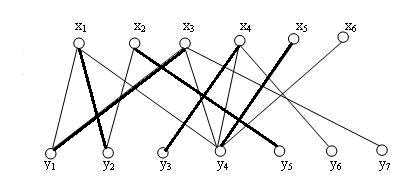
在二分图中,最大匹配是指选出尽可能多的边使得任意两边没有公共端点。
增广路
设 M M M为二分图 G G G已匹配的边的集合,若 P P P是图 G G G中一条连接两个未匹配顶点的路径(起点终点分别在两个集合),属于 M M M的边和不属于 M M M的边交替出现,则 P P P称为 M M M的一条增广路(直接匹配的边也是特殊的增广路)。
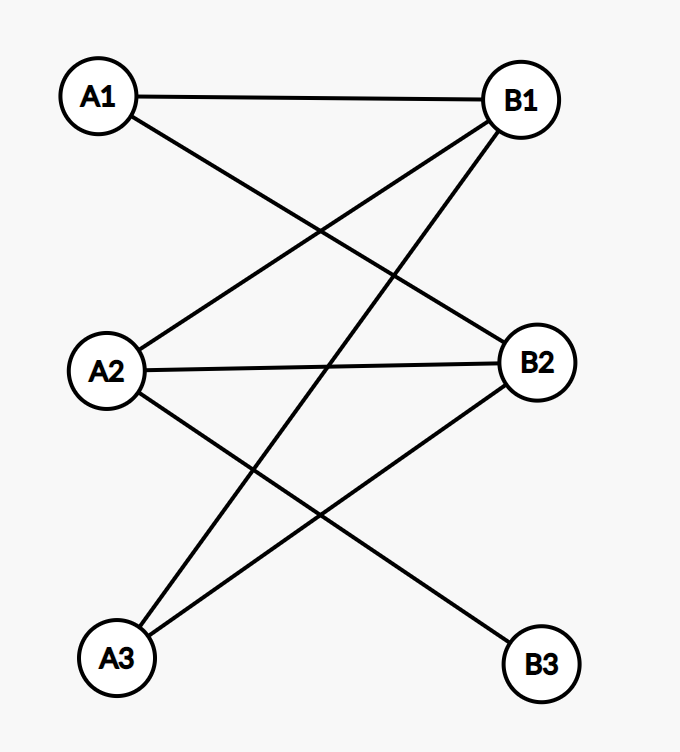
如下图所示,当 1 1 1和 A A A已经匹配,而尝试寻找 2 2 2的匹配时,发现它只能匹配 A A A:

然后尝试让 2 2 2匹配 A A A,这时再给 1 1 1找新的匹配的过程看做:从 2 2 2出发,遍历到 A A A;再从 A A A遍历到 1 1 1;最后遍历 A A A的未匹配的终点,即从 1 1 1到 B B B。那么如下图所示的起点终点确定,确定匹配的边和不能匹配的边交替出现的交错路,就称为增广路。

匈牙利算法
匈牙利算法是依据贪心思想的二分图最大匹配算法。
简单易懂的理解:对于给定的二分图,我们只需考虑左边或者右边的一个点集,然后枚举所有的点。对于当前枚举的点 u u u,考虑它所连向的点 v v v是否已经匹配:若没有匹配,则直接匹配;若已经匹配了 u ′ u' u′,我们采用的策略是暂时将 u u u和 v v v相连接,重新给 u ′ u' u′找匹配对象。即递归遍历 u ′ u' u′所有连向的点,如果能再次匹配到未匹配的 v ′ v' v′,则回溯修改沿途的所有的匹配,建立新的匹配关系。这时新的匹配数显然增加了 1 1 1,最终增加的所有匹配数即为答案。
增广路径下的理解:不难发现,如果需要得到最大匹配,就是给每个节点寻找增广路的过程。如果能找到增广路,那么答案增加,最终增加的次数即为答案。
时间复杂度 O ( n ∗ e ) O(n*e) O(n∗e), n n n为一边的点数, e e e为边数。
dfs模板
- m a t c h [ i ] match[i] match[i]:对于右点集编号为 i i i的点,匹配的左点集的编号。
- v i s [ i ] vis[i] vis[i]:右点集编号为 i i i的点在这次搜索中是否判断。
- g [ i ] g[i] g[i]:左点集编号为 j j j的点所连向的所有右点集的点。
int match[maxn];
bitset<maxn> vis;
vector<int> g[505];
int n; //左边的点数bool dfs(int u) {for (int i = 0; i < g[u].size(); i++) {int v = g[u][i];if (!vis[v]) {vis[v] = 1;if (match[v] == -1 || dfs(match[v])) {match[v] = u;return 1;}}}return 0;
}int hungary() {int ans = 0;memset(match, -1, sizeof match);for (int i = 1; i <= n; i++) {vis.reset();if (dfs(i)) ans++;}return ans;
}
Hopcroft-Karp算法
H K HK HK算法相对于匈牙利算法来说,每次都是增广一系列路径,因此更快。我们每次从所有未匹配的左部节点开始 B F S BFS BFS,进行距离标号。对于每个队列中的节点 X X X,考虑和它相邻的所有右部节点 Y Y Y,若 Y Y Y是一个未匹配的右部节点,则说明至少存在一条增广路,使用一个 b o o l bool bool变量 o k ok ok记录,以便之后增广;否则,将 Y Y Y的匹配节点加入到队列中顺便求出距离标号。当 B F S BFS BFS结束时,若不存在增广路,即 o k ok ok为 f a l s e false false,那么算法结束;否则对于每一个未匹配的左部节点 X X X执行匈牙利算法,注意在这里匈牙利算法中只需考虑满足 d x [ u ] + 1 = d y [ v ] dx[u]+1=dy[v] dx[u]+1=dy[v]的边 ( u , v ) (u,v) (u,v)。
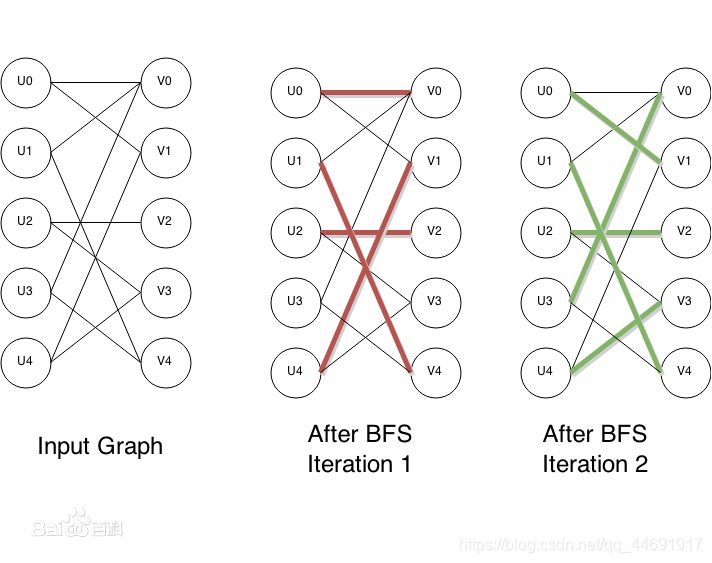
时间复杂度 O ( e n ) O(e\sqrt{n}) O(en)
模板
const int maxn = 5e4 + 10;int n1, n2; //左右部的节点数
int mx[maxn], my[maxn], dx[maxn], dy[maxn]; //左右部匹配的节点以及左右部顶点的距离
queue<int> q;
bitset<maxn> vis;
vector<int> g[maxn];bool find(int u) {for (int i = 0; i < g[u].size(); i++) {int v = g[u][i];if (!vis[v] && dy[v] == dx[u] + 1) {vis[v] = 1;if (!my[v] || find(my[v])) {mx[u] = v, my[v] = u;return true;}}}return false;
}int matching() {memset(mx, 0, sizeof mx);memset(my, 0, sizeof my);int ans = 0;while (1) {bool ok = 0;while (!q.empty()) q.pop();memset(dx, 0, sizeof dx);memset(dy, 0, sizeof dy); for (int i = 1; i <= n1; i++) {if (!mx[i]) q.push(i);}while (!q.empty()) {int u = q.front();q.pop();for (int i = 0; i < g[u].size(); i++) {int v = g[u][i];if (!dy[v]) {dy[v] = dx[u] + 1;if (my[v]) {dx[my[v]] = dy[v] + 1;q.push(my[v]);} else ok = 1;}}}if (!ok) break;vis.reset();for (int i = 1; i <= n1; i++)if (!mx[i] && find(i)) ans++;}return ans;
}