SetupFactory是一款能够用于工程向导、自定义对话框、生成MD5序列化以及两百多个功能函数的脚步编辑器、授权支持等等众多的特性。总体来说使用起来比较简单，在这里俺就介绍一下如何打包C#项目，至于其他使用如果有时间后续俺会再介绍的。

在这里俺使用的SetupFactory9进行演示（各位大佬如果需要安装包，可以私俺或者留言，俺肯定欣然为各位大佬提供安装包）：

1.双击桌面图标或者安装路径下的exe文件进入主界面，主界面效果图如下所示：

2.创建一个新项目或者打开一个已经存在的项目

3.依次填好公司名称、产品名称、软件版本号、公司网址后点击"下一步":

4.选择安装包程序的位数：32位和64位，具体如何选择就要看各位看客的需求了，俺这里考虑到xp系统就选择了32位的安装包，截图如下：

5.指定要打包的文件所在文件夹位置：

6.选择安装包安装样式，此处setupFactory提供两种方式，一种是setupfactory内置提供的多种模板，另一种就是用户进行自定义设计，此处为了方便就选用了第一种方式：

7.选择安装界面模板

8.选择安装包语言，这个就要看各位大佬的选择了：

9.选择软件环境，到后期会出现一些问题，俺在后面会提到的，俺这里选择的是.net4.0的环境：

10.选择支持系统和其它一些细节

11.进入具体设置页面：

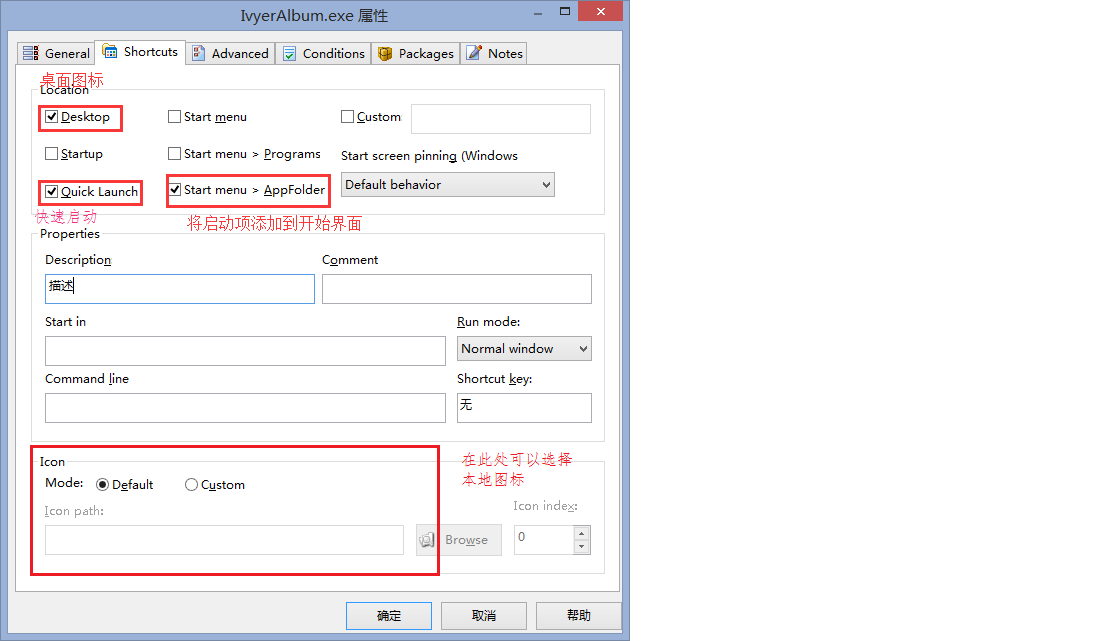
12.在文件列表中找到.exe文件后，双击.exe文件进入软件启动细节设置：

设置快速启动等等.....

13.对软件安装过程中各个展现Srceen进行细节设置：

此处就对安装之前的各项设置进行简单介绍一下，双击"Before Installing" ：

输入软件安装许可协议

14.卸载时设置：

双击“Settings”，进入设置页面：

15.开始生成安装包

此处选择生成.exe文件，当然setupFactory还支持CD、DVD、web等方式：

点击“Next”继续进行设置安装包输出位置：

点击“Next”开始生成安装包。是不是认为这样子就没得问题了呢？当然不可能滴，接着就会报出一个错误滴：

各位看客应该懂了吧，是setupfactory找不到你之前选择的软件运行环境了（之前选择的为.net4.0），对于这些setup是不会为你提供的，需要自行下载并放置到指定目录下：

放置好了吧，接着回去重新build试试看哦！

好了，打包过程到此算是暂时完成了！谢谢