C语言实现雅克比迭代法求根

问题描述

设方程组$Ax=b$的系数矩阵$A$非奇异 ，且$a_{ii}\ne 0$将$A$分裂为：$$A=D+L+U$$
$D=diag(a_{11},a_{22},\cdots a_{nn})$, $L$和$U$分别是将$A$对角元素置为$0$的下三角和上三角矩阵，进行一系列转化形成迭代格式可求解方程组。

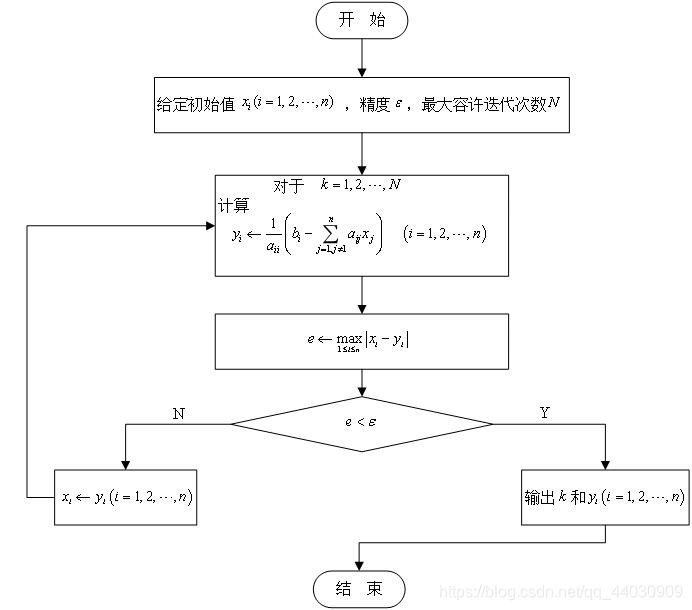
算法思想

将方程组
$$\sum _{i=1}^{i=n}{a}_{ij}{x}_i=b_i,i=1,2...,n$$
乘以$\frac{1}{a_{ii}}$，得到等价方程组
$$x_i=\frac{1}{a_{ii}}(b_i-\sum _{i=1}^{i=n}{b}_i-a_{ij}{x}_i)$$
简记为$x=Bx+f$.
其中，$B=I-D^{-1}=-D^{-1}(L+U),f=D^{-1}b$
我们称 $\phi (x)=Bx+f$为迭代函数，任取初始向量 $x=x^{(0)}$，按照 $x^{(k+1)}=B{x}^{(k)}+f$形成的迭代格式，称这种迭代格式为雅克比迭代法。

C语言程序

#include <stdio.h>
#include <stdlib.h>
#include<math.h>
#define MaxSize 100
double A[MaxSize][MaxSize];
double B[MaxSize];
double C[MaxSize][MaxSize];
double D[MaxSize][MaxSize];//储存D逆
double E[MaxSize][MaxSize];//储存-(D-1)*(L+U)
double F[MaxSize];//(D-1)*B
double X[MaxSize];
double X1[MaxSize];
double Y[MaxSize];
#define e 1e-6//10的负6次方
int n;//矩阵尺寸大小
//所有迭代格式X(k+1)=B*X(k)+F,B范数<1,必收敛，B范数>1,未必发散
//雅克比迭代只适用于A[i][i]非0
void InitMatrix()
{int i,j;for(i=0;i<n;i++)for(j=0;j<n;j++){if(i==j){D[i][j]=1/A[i][i];E[i][j]=0;}if(i<j)E[i][j]=A[i][j];if(i>j)E[i][j]=A[i][j];}}void Jacobi()
{int i,j,k,r;double sum1,sum2,sum4=0;for(i=0;i<n;i++)for(j=0;j<n;j++){sum1=0;for(k=0;k<n;k++)//矩阵运算{sum1=sum1+D[i][k]*E[k][j];}E[i][j]=-sum1;//(D-1)*(L+U)}//求E的F范数，判断是否收敛//E的F范数>1,不一定发散;但是E的F范数<1,一定收敛for(i=0;i<n;i++)for(j=0;j<n;j++)sum4=sum4+pow(E[i][j],2);if(sqrt(sum4)<1)printf("/*****B矩阵F范数<1，必有数值解！*****/\n");elseprintf("/*****B矩阵F范数>1，不一定有数值解！*****/\n");for(i=0;i<n;i++){sum2=0;for(k=0;k<n;k++){sum2=sum2+D[i][k]*B[k];}F[i]=sum2;//(D-1)*B}//X迭代for(r=1;r<100;r++){int flag=0;double sum3;for(i=0;i<n;i++)X1[i]=X[i];//储存上一次迭代运算结果,必须在此处储存for(i=0;i<n;i++){sum3=0;for(k=0;k<n;k++){sum3=sum3+E[i][k]*X1[k];}X[i]=F[i]+sum3;//更新X[i]}for(j=0;j<n;j++)if(fabs(X[j]-X1[j])<e)//abs整型求绝对值,fabs浮点型求绝对值flag++;if(flag==n){printf("迭代第%d次满足精度！\n",r);break;}printf("第%d次迭代向量X：\n",r);for(i=0;i<n;i++)printf("%lf\n",X[i]);}}void input()
{int i,j;printf("请输入系数矩阵A：\n");for(i=0;i<n;i++)for(j=0;j<n;j++)scanf("%lf",&A[i][j]);printf("请输入向量B：\n");for(i=0;i<n;i++)scanf("%lf",&B[i]);printf("请输入初始向量X：\n");for(i=0;i<n;i++)scanf("%lf",&X[i]);
}
void print()
{int i,j;printf("方程组的近似解：\n");for(i=0;i<n;i++)printf("%lf\n",X[i]);
}int main()
{void InitMatrix();void Jacobi();void input();void print();printf("请输入矩阵行数：\n");scanf("%d",&n);printf("\n");input();InitMatrix();Jacobi();print();return 0;
}

实验结果

$$\{\begin{array}{l}{x}_1+2x_2-2x_3=1\\ x_1+x_2+x_3=3\\ 2x_1+2x_2+x_3=5\end{array}$$
初始向量为：$x^{(0)}=(0,0,0{)}^T$