雅可比迭代法
设有线性方程组
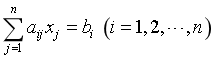 (1)
(1)
其矩阵形式为
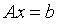
设系数矩阵A为非奇异矩阵,且
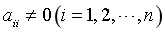
从式(1)的第个方程中解出,得其等价形式
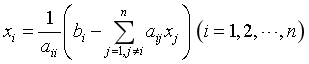 (2)
(2)
取初始向量
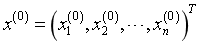
对式(2)应用迭代法,建立相应的迭代公式
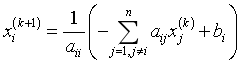 (3)
(3)
也可记为矩阵形式
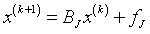 (4)
(4)
若将系数矩阵A分解为
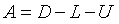
式中
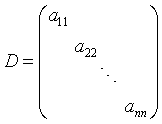

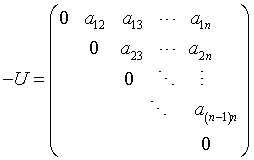
则
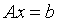
变为
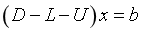
得
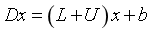
于是有
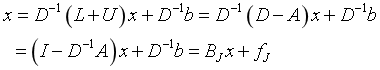
所以式(4)中的
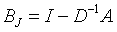
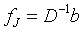
式(3)和式(4)分别称为雅可比(Jacobi)迭代法的分量形式和矩阵形式,分量形式用于编程计算,矩阵形式用于讨论迭代法的收敛性。
算法流程图
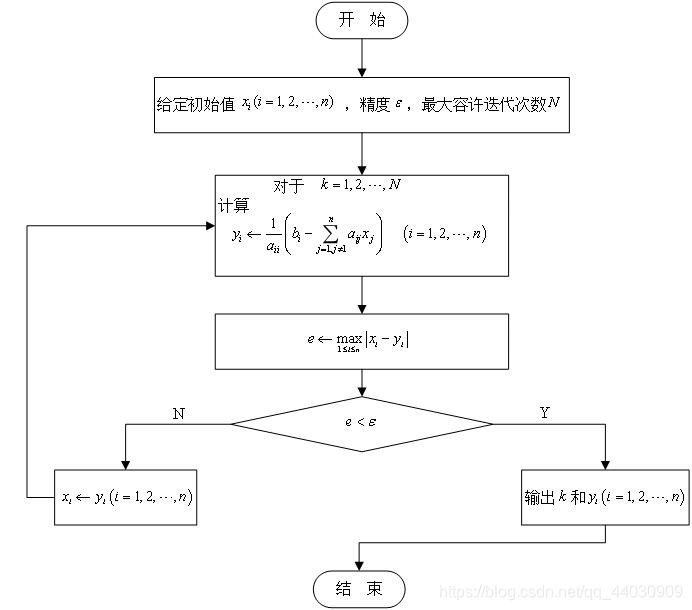
首先编写MATLAB函数文件agui_jacobi.m:
function x= agui_jacobi(a,b)
% a为系数矩阵,b为右端变量,x0为初始向量(默认为零向量)
% e为精度(默认为1e-6),N为最大迭代次数(默认值为100),x为返回解向量
format long
n=length(b);
N=100;
e=1e-6;
x0=zeros(n,1);
x=x0;
x0=x+2*e;
k=0;
d=diag(diag(a));
l=-tril(a,-1);
u=-tril(a,1);
while norm(x0-x,inf)>e&k<Nk=k+1;x0=x;x=inv(d)*(1+u)*x+inv(d)*b;kdisp(x')
end
if k==N warning('已达最大迭代次数');end
end