之前写过不少关于微分和导数的文章:
-
微分是什么?
-
dx,dy是什么?
-
微分和导数的关系是什么?
-
今天这篇文章再换一个角度来谈论微分和导数,让我们从微分出现的原因说起。
1 微分出现的原因
出于种种原因,我们可能想去求曲线的长度、曲面梯形的面积:
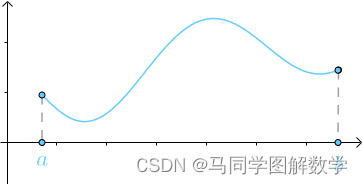
求 和
之间的曲线长度
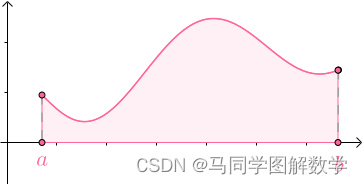
求 和
之间的曲边梯形的面积
求解思路是这样的,以求曲线长度为例,将曲线分为多个部分,每一部分都用切线来近似曲线:
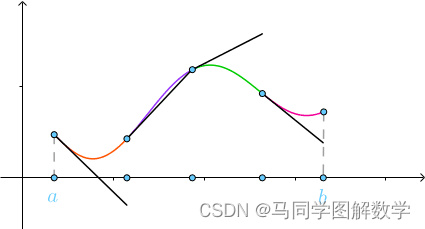
划分的越细,直到划分为无穷多份,最终这些切线的长度加起来就是曲线的长度:
求曲边梯形面积也是类似的,用小矩形来近似曲边梯形的面积,随着小矩形的增多最终得到曲边梯形的面积:
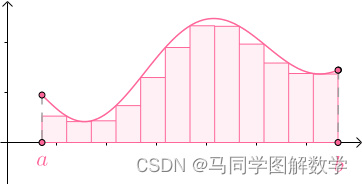
上面的思想就是微积分的核心思想,“以直代曲”。曲线长度、曲边梯形就是“曲”,切线、小矩形就是用来近似(代替)的“直”,这种“直”就是微分。关于这里还不了解的可以看“微分是什么?”这篇文章。
2 微分与导数
先不谈曲边梯形,本节先来回答曲线的微分是什么,也就是可以近似曲线的直线是什么?
2.1 几何分析
下面结合几何来理清一下求解的思路。假设有曲线 和直线
,如果两者完全相等,那么有:
![]()
很显然这在整个曲线和直线上是做不到的,但肯定可以做到在某点上相等,比如让它们在 点相等,从几何上看就是曲线
和直线
在
点相交:

下面要更进一步,不过不要太贪心,只希望两者在 附近尽量相等。比如像下图一样,在
的区间内,曲线
和直线
相差很小:
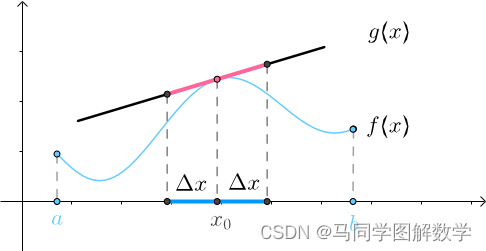
这点如果可以做到,那就可以按照上一节说的,将曲线分成n份,每份都用各自的微分来近似。
2.2 代数分析
通过几何分析,思路已经理清楚了,要找的微分(直线)需要满足以下两点:
(1)曲线 和直线
要交于
点。假设直线
的斜率为
,那么根据点斜式,可得直线函数:
这里面就是 还未知,求出了
就得到了想要的直线,也就得到了微分。
(2)曲线 和直线
要在
的区间内尽可能相等。用代数表示即为:
有约等号的式子是没法计算的,引入高阶无穷小 可以将约等号去掉:
高阶无穷小 的意思就是在
这个范围内无限的接近于 0。至于为什么它无限接近于 0,以及为什么是高阶无穷小,在文章的最后会进行补充说明。
2.3 解出直线的斜率
经过上面的分析我们有了:
这已经足够让我们解出直线的斜率 了。注意到
,可以进行如下变形:
两侧取极限可得:
略微作一下化简可得:
至此我们就求出了 ,也就找到了
的微分(直线
的形式还需要变一下才是真正的微分,关于这点可以参考“dx,dy是什么?”这篇文章)。
这个 在微积分中又有一个专门的名字,称为
的导数。
如果存在(因为
是通过极限求得的,这个极限有不存在的可能),那么就称
可导。
上面的思路还可以进一步思考,如果要找最接近曲线 的多项式曲线呢?这会得到泰勒公式,就留给大家作课后习题吧。
3 补充说明
这里补充说明两点:
(1)高阶无穷小 为什么表示在
的区间内无限接近于 0 ?这是因为它满足:
上面这个极限式意味着 越小,也就是越接近于
点,
越接近于 0。用动画表示就是:

上图中绿线就是曲线 ,蓝线为微分,可以看到随着
缩小,两者之间的距离
也无限接近于 0。
(2)为什么一定要高阶无穷小?同阶无穷小行不行?关于这点可以参考“为什么算出来的圆周率 π 等于 4 ?”这篇文章。