目录

一、求常系数线性齐次微分方程的通解

二、可分离变量的一阶微分方程

三、齐次方程

四、一阶线性微分方程

五、 可降解的高阶微分方程

六、常系数非齐次线性微分方程的特解形式 

---

注：//之后的都是注释，不是过程。

一、求常系数线性齐次微分方程的通解

1.一般形式：y''+py'+qy=0。

2.齐次：“齐次”的含义就是次数相等，y''+py'+qy=0都是一次幂，所以是齐次线性微分方程，如果说加上一个常数c，变为y''+py'+qy+c=0，那么这个c是可以看作cy⁰，y的零次幂，就不是齐次微分方程了。

3.特征方程：有几阶导就看作几次幂。

4.求出特征根：

① 若有两个不同的特征根，通解y=C1*e^r1x+C2*e^r2x（对应例2）

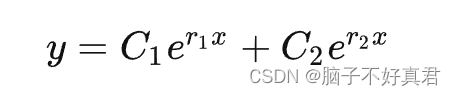
②若有两个相同的特征根，通解y=(C1+C2x)e^rx（对应例3）

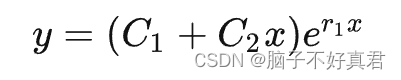
③若有一对共轭复根，通解y=e^αx(C1cosβx+C2sinβx)（对应例4）

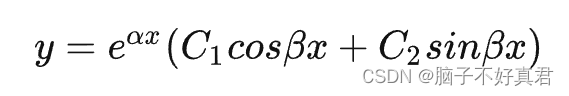
例1：求y'=y的通解。

解：特征方程为r-1=0∴r1=1∴通解y=e^x

例2：求y''-2y'-3y=0的通解。

解：特征方程为r^2-2r-3=0//十字相乘法：1   -3//1    1∴r1=3，r2=-1∴通解为：y=C1e^3x+C2e^-x

例3：求y''+2y'+y=0的通解。

例4：求y''-2y'+5y=0的通解。

 

二、可分离变量的一阶微分方程

解题步骤：

1.把y’写作dy/dx。

2.移项，使等式两边分别全为x，全为y。

3.对两边积分。

例1：求y'=2x的通解。

解：∵dy/dx=2x ∴dy=2xdx ∴∫dy=∫2xdx∴y=x^2+C

例2：求y'=e^2x-y，y|x=0=0的特解。

解：∵dy/dx=e^2x*e^-y  ∴e^ydy=e^2xdx  ∴∫e^ydy=∫e^2xdx  ∴e^y=1/2*e^2x+C  代入x=0,y=0得C=1/2  ∴e^y=1/2*e^2x+1/2  两边同取对数得 y=ln(e^2x+1)/2

例3：求xy'-ylny=0的通解。

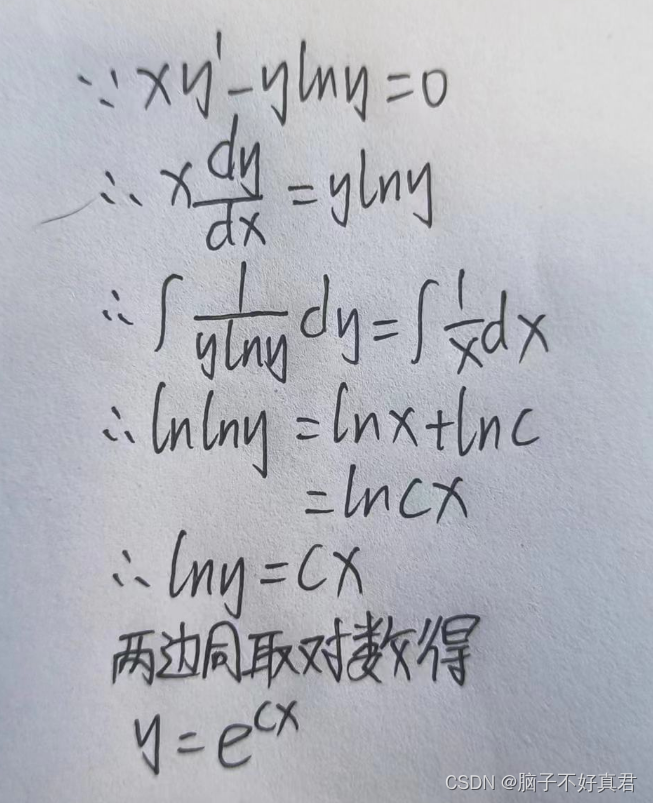
三、齐次方程

出现或者能产生y/x的情况使用，实际上就是换元法，步骤：

1.设u=y/x。

2.所以y=ux、dy/dx=u+x*du/dx，将两者代入方程(化为y/x形式的那个方程)。

3.分离变量的方法。

例1：求齐次方程xy'=ylny/x的通解。

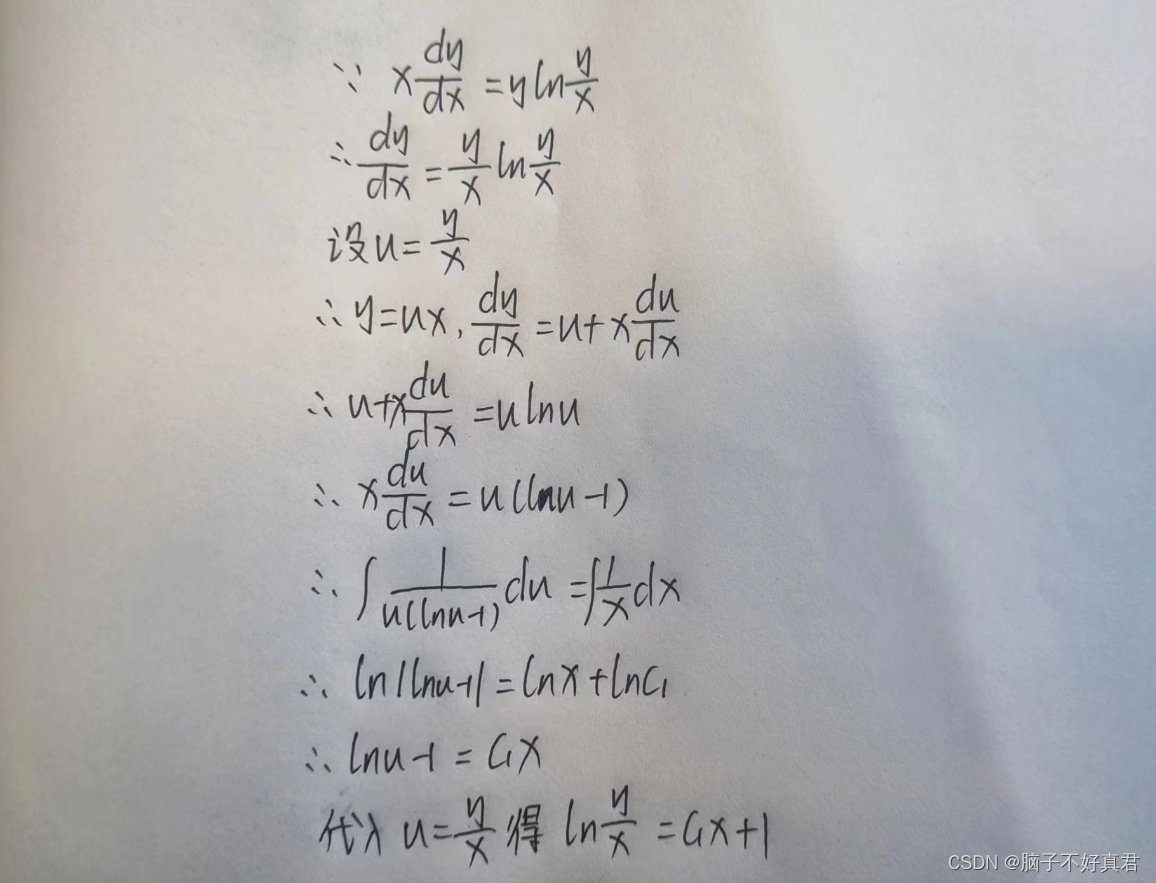
四、一阶线性微分方程

1.方程：y'+P(x)y=Q(x)

2.公式：

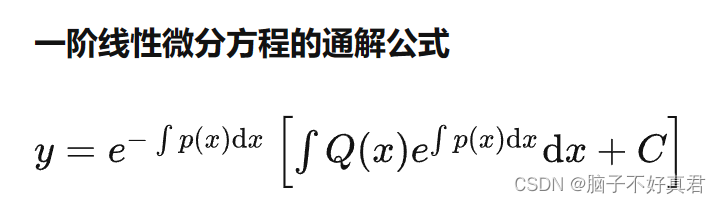
例1： 求y'+y=e^x的通解。

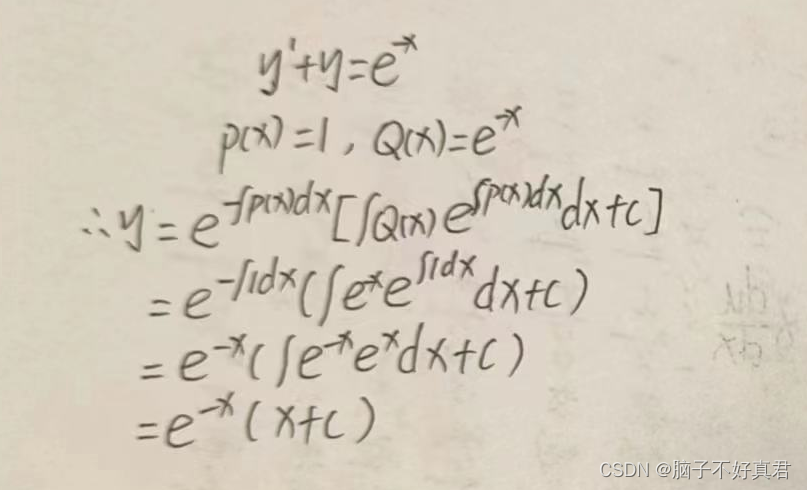
例2：y'-ytanx=secx的通解。

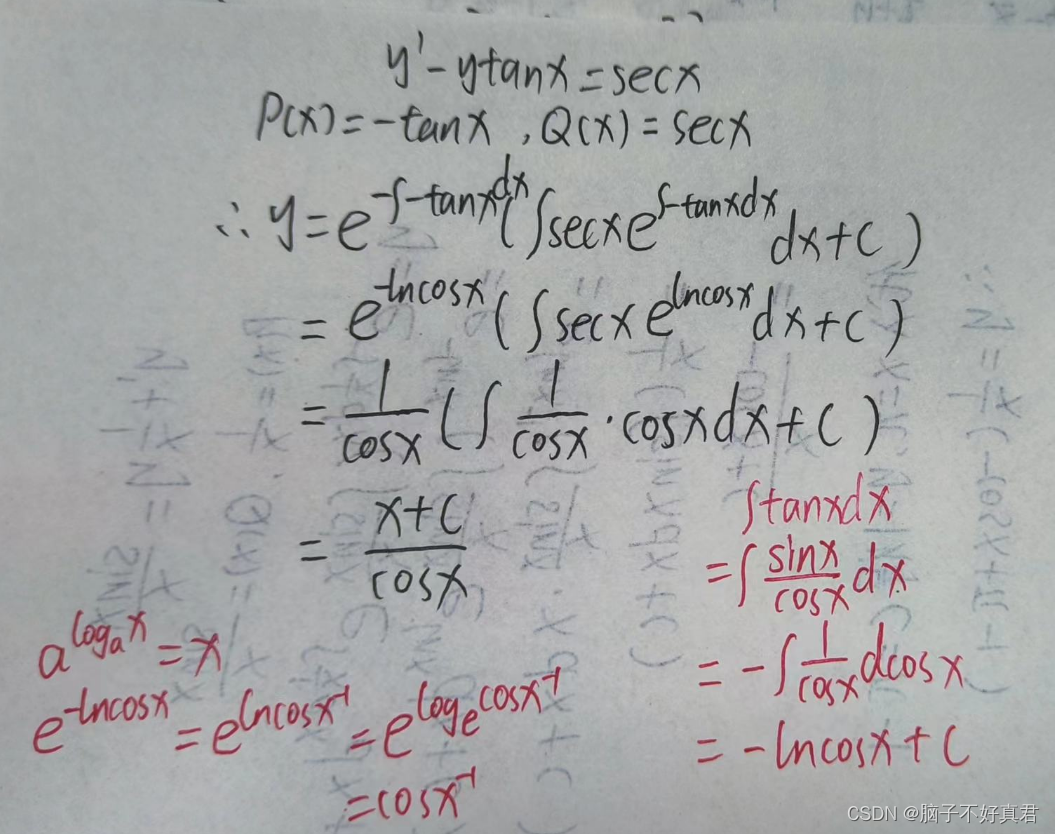
例3：y'+y/x=sinx/x，y|x=π=1的特解。

五、 可降解的高阶微分方程

1.缺y型的形式：y''=f(x,y')

解题方法：令y'=p  y''=p'

2.缺x型的形式：y''=f(y,y')

解题方法：令y'=p  y''=p*dp/dy

例1：求(1+x^2)y''=2xy'的通解。(移项后符合y''=f(x,y')，是缺y型)

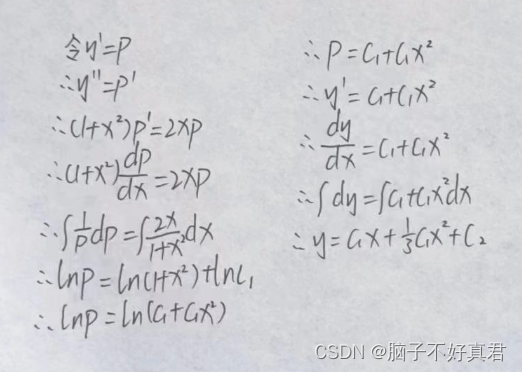
例2：求yy''-y'^2=0的通解。(移项后符合y''=f(y,y')，是缺x型)

六、常系数非齐次线性微分方程的特解形式 

1.一般形式：y''+py'+qy=f(x)

2.解题步骤：

①把f(x)看作0，视为齐次方程。

②写出该齐次方程的特征方程，求出特征根。

③与λ(例题中解释)相比，若λ=r1=r2（重根）；若λ=r1或者r2（单根）；若λ≠r1,r2（无根）。

④重根k=2；单根k=1；无根k=0。

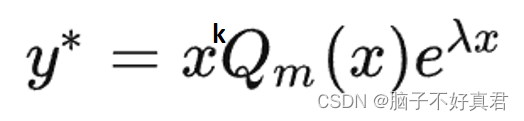
 ⑤Q(m)的情况：看等式右边x的次数，一次幂设Q(m)=ax+b；二次幂设Q(m)=ax^2+bx+c；没有x设Q(m)=a。

例1：求y''-5y'+6y=xe^2x的特解形式。

例2：求y''+5y'+4y=6-2x的特解形式。

大家放心，草稿纸剩下的边边角角我都会用起来的，绝不会浪费纸张。如果有错误望指出。