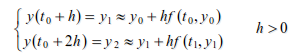微分滤波器总结

article/2025/4/3 9:02:39

微分滤波器

本质：逻辑上，平滑使用的是积分，锐化则应使用微分。

1.索贝尔（Sobel）导数

索贝尔算子可以实现任意阶导数和混合偏导数。
本质：求得图像的一阶或二阶近似梯度图像。

void Sobel( InputArray src, OutputArray dst, int ddepth,int dx, int dy, int ksize = 3,double scale = 1, double delta = 0,int borderType = BORDER_DEFAULT );
参数：src：源图像。
dst：目标图像。
ddepth：图像的深度和类型。
dx：x方向求导次数。
dy：y方向求导次数。
ksize：滤波器尺寸。
scale：结果线性处理系数。
delta：结构偏移处理系数。
borderType：边界添加类型。
其中：dst=sacle*dst1+delta

以求图像一阶梯度图像，最小模板即3X3为例：
首先：离散函数x,y方向上的梯度大小为
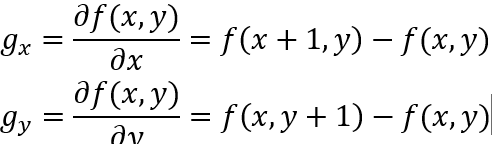
在这里插入图片描述
二维梯度大小为：
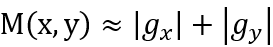
M(x,y)≈|g_x |+|g_y |
实际计算时：常常取：
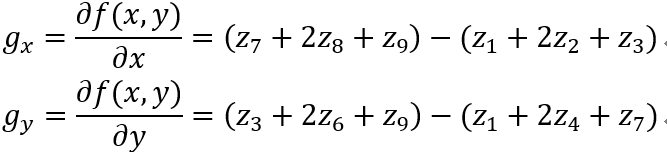
g_x=(∂f(x,y))/∂x=(z_7+〖2z〗_8+z_9 )-(z_1+〖2z〗_2+z_3)g_y=(∂f(x,y))/∂y=(z_3+〖2z〗_6+z_9 )-(z_1+〖2z〗_4+z_7)
z1 z2 z3z4 z5 z6z7 z8 z9
最终：

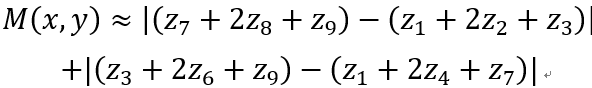
从离散函数求导的角度来说，核的size越大自然越接近导数，但对于像素值剧烈变换的像素点来说，大Size反而会使结果发生较大偏差。

2.Scharr滤波器

类似于Sobel，只不过核的Size被固定为3x3。

void Scharr( InputArray src, OutputArray dst, int ddepth,int dx, int dy, double scale = 1, double delta = 0,int borderType = BORDER_DEFAULT );
参数：src：源图像。
dst：目标图像。
ddepth：图像的深度和类型。
dx：x方向求导次数。
dy：y方向求导次数。
scale：结果线性处理系数。
delta：结构偏移处理系数。
borderType：边界添加类型

3. 拉普拉斯变换

由微分的图像信息得知：图像的一阶微分产生较粗的边缘，二阶微分产生由零分开的一个像素宽的双边缘。在增强细节方面二阶微分比一阶微分好得多。
拉普拉斯算子（二阶微分）：
∇2=(∂2 f)/(∂x^2 )+(∂^2 f)/(∂y^2 )∇^2=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)
拉普拉斯算子应用：突出被大值包围的点或者被小值包围的点。同时可用于边缘检测。

    void Laplacian( InputArray src, OutputArray dst, int ddepth,int ksize = 1, double scale = 1, double delta = 0,int borderType = BORDER_DEFAULT );参数：src：源图像。
dst：目标图像。
ddepth：图像的深度和类型。
ksize：核尺寸。
scale：结果线性处理系数。
delta：结构偏移处理系数。
borderType：边界添加类型