贝塔分布例子（转）

 

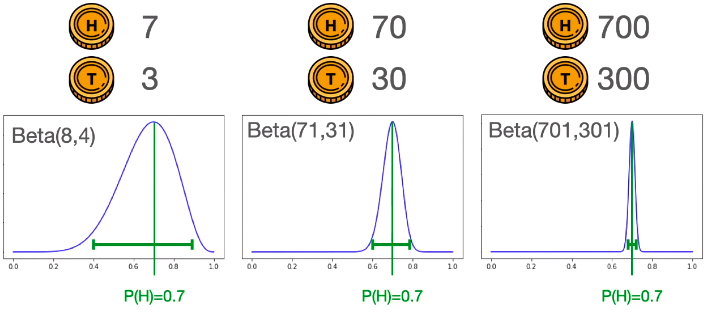
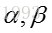古语有云，“学好数理化，走遍天下都不怕。”

 

人工智能时代尤其如此。

 

比如，写上几句基础的数学概念，天上就能掉下一个工作来……这是真事。

 

学概率的时候，我们会反复来理解什么是正态分布，什么是均匀分布，什么是二项分布，什么是贝塔分布……不知在座的各位是否还能记起当时做过的习题？是否还能通俗地讲解一下这些概念？

 

在Stack Overflow，有位学机器学习的同学理解不了贝塔分布，希望有人能帮他解答下。刚好，正在学生物信息学博士的David Robinson现身说法，用一个有关棒球运动的统计数据来解释这个概念。这位博士纯粹是为了消磨时间，觉得好玩。

 

不过，Stack Overflow数据科学团队的Jason Punyon读完David Robinson的解答后，觉得解释很赞，他在内部会议上突发奇想：

 

 

“哇！咱们干脆雇了这哥们儿吧。”

 

于是，一份公开的邀请不期而至：我们十分期待你能拜访一下Stack Overflow。

 

 

在好奇心的驱使下，原本打算博士毕业后研究计算生物学的David Robinson，鬼使神差地拜访了这家科技公司。一次拜访、几周面试，Stack Overflow提供给他一个无法拒绝的工作机会，David Robinson从计算生物学博士变成了一个数据科学家。

 

你一定特别好奇，这到底是个怎样的问题，直接就让这位博士拿到了数据科学家的offer？David Robinson的解释到底又有多精彩？现在我们让来看看这个问题。

 

 

问题

 

 

首先声明，我并不是统计学家，只是一名软件工程师。我所掌握的大部分统计学知识都来自于自学，因此对于一些别人觉得很简单的概念，我可能会觉得很难理解。因此我希望答案能尽量通俗易懂，少一些专业名词而多一些形象解释。

 

我之前试图想弄清楚贝塔分布(beta distribution)的本质——它能用于做什么以及如何解释它的应用场景？

 

例如，当我们谈正态分布时，可以将它描述成火车的到达时间：大多数情况下火车正点到站，有时候会早1分钟或者迟1分钟，但是早20分钟或者迟20分钟的情况则非常罕见；均匀分布可以描述为彩票中奖的机会事件；二项分布可以描述成抛硬币事件等等。那么，贝塔分布有这样的直观解释吗？

 

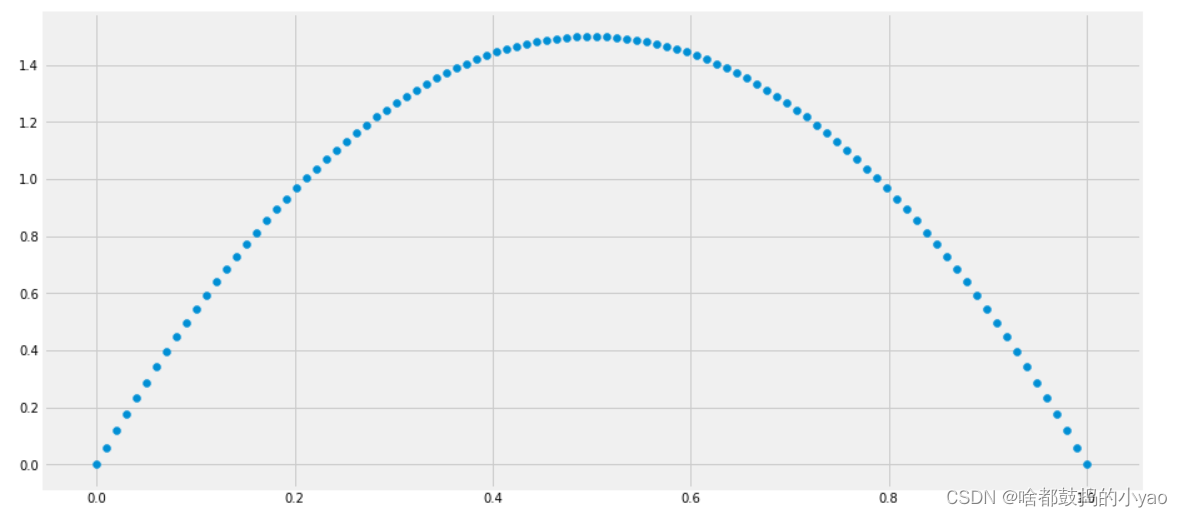
例如 α=.99，β=.5，贝塔分布B(α,β)如下图所示（使用R生成）：

 

 

 

那么这个图代表什么意思？Y轴是一个概率密度，那么X轴呢？

 

答案可以基于这个例子来解释，或者任何其他的也行。我将感激不尽。

 

David Robinson 解释如下：

 

简而言之，贝塔分布可以看作是一个概率的分布，也就是说，当我们不知道一个东西的具体概率是多少时，它给出了所有概率出现的可能性大小。下面结合一个应用场景来理解：

 

熟悉棒球运动的都知道一个指标就是棒球击球率（batting average-http://en.wikipedia.org/wiki/Batting_average%22），就是用一个运动员击中的球数除以总的击球数（因此它是一个0到1之间的百分比）。我们一般认为0.266是一个平均的击球水平，而如果击球率达到0.3就会被认为非常优秀了。

 

假设有一个棒球运动员，现在我们想预测他整个赛季的棒球击球率如何。你可能就会直接计算他目前的棒球击球率，用击中数除以击球数，但这在赛季开始阶段时是很不合理的！假如这个运动员就打了一次，还中了，那么他的击球率就是100%，如果他没中，那么就是0%。甚至打5、6次的时候，也可能运气爆棚全中击球率100%，或者运气很糟击球率0%。无论如何，基于这些来做预测是不合理的。

 

那么，为什么用前几次击中来预测整个赛季击球率不合理呢？当运动员首次击球没中时，为什么没人认为他整个赛季都会一次不中？因为我们有先验期望。根据历史信息，我们知道击球率一般会在0.215到0.36之间。如果一个运动员一开始打了几次没中，那么我们知道他可能最终成绩会比平均稍微差一点，但是一般不可能会偏离上述区间。

 

对于这个击球率问题，我们可以用二项分布(https://en.wikipedia.org/wiki/Binomial_distribution)表示（一系列的成功或失败事件），一个最好的方法来表示这些先验期望（统计中称为先验（prior））就是贝塔分布，这表示在运动员打球之前，我们就对他的击球率有了一个大概范围的预测。贝塔分布的定义域为(0, 1)，与概率是一样的。我们下面继续解释为什么贝塔分布用在这个任务上是合理的。

 

假设我们预计运动员整个赛季的击球率大概是0.27左右，范围大概是在0.21到0.35之间。那么用贝塔分布来表示，我们可以取参数 α==81，β==219。

 

curve(dbeta(x, 81, 219))

 

 

之所以取这两个参数，原因如下：

 

• 贝塔分布的均值 

   

 

 

• 从上图中可以看出，这个分布主要落在(0.2, 0.35)之间，这是从经验得到的合理范围。

 

你问在贝塔分布的密度图上x轴代表什么，在这里，x轴代表运动员的击球率。注意到在这个例子里，不仅y轴是代表概率（确切说是概率密度），x轴也是（击球率是击中次数的概率分布）。因此贝塔分布可以看作一个概率的分布。

 

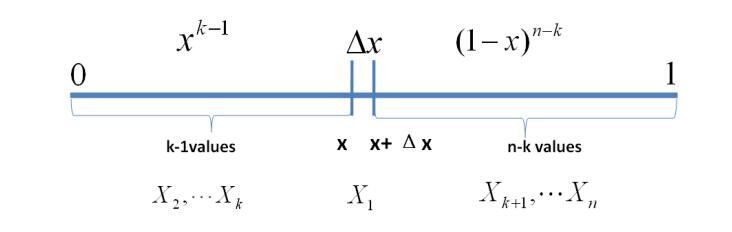
接下来解释为什么贝塔分布适合这个例子。假设运动员一次击中，那么现在他本赛季的记录是“1次打中；1次打击”。那么我们更新我们的概率分布，让概率曲线做一些移动来反应我们的新信息。这里涉及一些数学上的证明(点此查看-https://en.wikipedia.org/wiki/Conjugate_prior#Example)，但是结论非常简单。新的贝塔分布为：

 

 

其中 α0和β0是初始参数，在这里是81和219。所以，在这个例子里，增加了1（击中了一次），没有增加（没有失误）。因此新的贝塔分布为Beta(81+1,219)，如下图：

 

 

curve(dbeta(x, 82, 219))

 

 

 

可以看到这个分布与原来相比并没有什么肉眼可见的变化，这是因为仅一次击中球并不能太说明什么问题。

 

然而，随着整个赛季运动员逐渐进行比赛，这个曲线也会逐渐移动以匹配最新的数据。由于我们拥有了更多的数据，因此曲线（击球率范围）会逐渐变窄。假设赛季过半时，运动员一共打了300次，其中击中100次。那么新的贝塔分布是Beta(81+100,219+200)，如下图：

 

 

curve(dbeta(x, 81+100, 219+200))

 

 

可以看出，曲线现在更尖而且往右移动了（击球率更高），由此我们对于运动员的击球率有了更好的了解。

 

根据新的贝塔分布，我们得到的期望值通常也是我们的新的估计。贝塔分布的期望值计算公式是。因此新的贝塔分布的期望值为，注意到这个值比直接预估要低，但是比赛季开始时的预计要高。

 

你可能已经注意到了，这个公式就相当于给运动员的击中次数添加了“初始值”，相当于在赛季开始前，运动员已经有81次击中219次不中的记录。

 

因此，在我们事先不知道概率是什么但又有一些合理的猜测时，贝塔分布能够很好地表示为一个概率的分布。

 

就这样，靠着一道数学题，就拿到了数据科学家的职位。做机器学习，你的数学准备好吗？

 

 

 

 

转自：https://mp.weixin.qq.com/s/ZEoxYPgenFgzHuNnI2IieQ