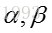全文共 1897 字，22 幅图，

预计阅读时间 10 分钟。

本文是「小孩都看得懂」系列的第十五篇，本系列的特点是内容不长，碎片时间完全可以看完，但我背后付出的心血却不少。喜欢就好！

1. 小孩都看得懂的神经网络

2. 小孩都看得懂的推荐系统

3. 小孩都看得懂的逐步提升

4. 小孩都看得懂的聚类

5. 小孩都看得懂的主成分分析

6. 小孩都看得懂的循环神经网络

7. 小孩都看得懂的 Embedding

8. 小孩都看得懂的熵、交叉熵和 KL 散度

9. 小孩都看得懂的 p-value

10. 小孩都看得懂的假设检验

11. 小孩都看得懂的基尼不纯度

12. 小孩都看得懂的 ROC

13. 小孩都看得懂的 SVD

14. 小孩都看得懂的 SVD 2

15. 小孩都看得懂的 GMM

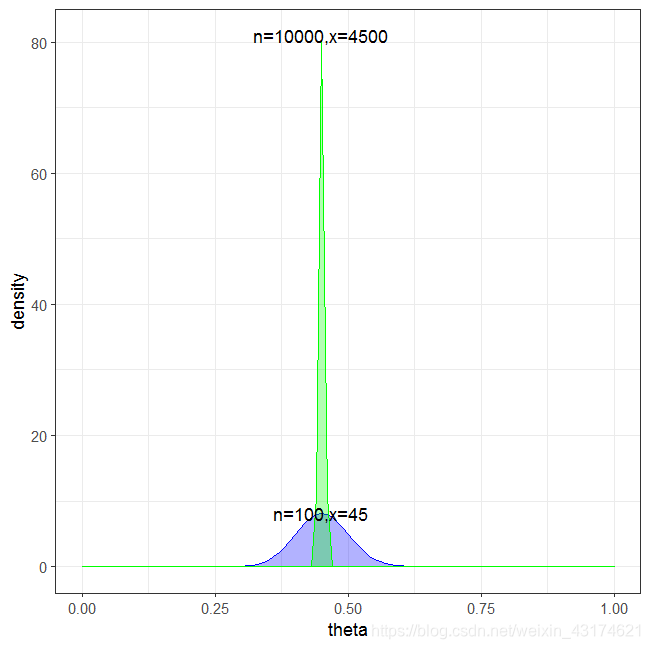
16. 小孩都看得懂的贝塔分布
    

0

贝塔分布 (beta distribution) 对概率建模得到的一个概率分布。听起来很绕口，下面看一个简单示例。

1

硬币问题

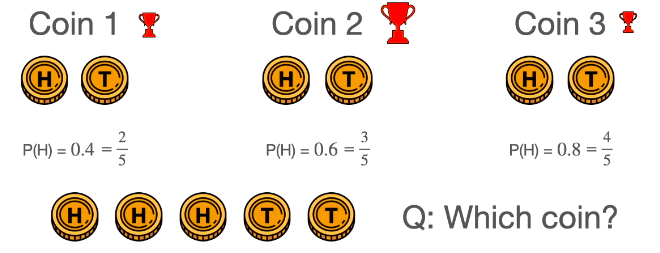
三个有偏 (biased) 硬币，丢它们落下来正面的概率分别是 0.4, 0.6 和 0.8。

如果随机选一个硬币，丢五次，得到“正正正反反 (HHHTT)”，问选中的是哪一个硬币？

2

硬币 2 的正面概率是 0.6 (3/5)，而丢 5 次 3 次朝上正好符合这个 3/5 的概率，那么应该是硬币 2。

但是选中的 100% 的是硬币 2 么？不是！硬币 1 和 3 也有可能被选中，只不过给定 “HHHTT”，选中的概率比选硬币 2 要小。  

要点：给定 HHHTT，硬币 2 最有可能被选中，而硬币 1 和 3 被选中的可能性小一些。没有绝对的，都是概率问题。

3

现在来计算出现 HHHTT 的概率。

• 硬币 1：0.43 × 0.62 = 0.0230

• 硬币 2：0.63 × 0.42 = 0.0346

• 硬币 3：0.83 × 0.22 = 0.0205

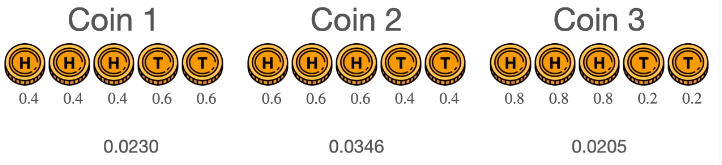
最后标准化使得三个概率总和为 1，注意分母是三个概率的和 (spoil alert: 这个概率和贝塔函数有联系)。

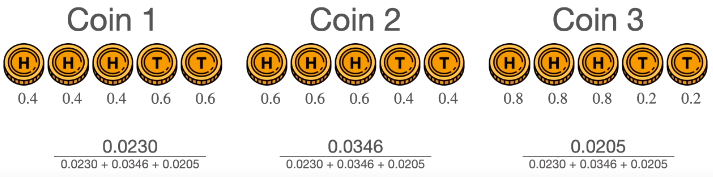
最终得到选中每个硬币的概率为 0.295, 0.443 和 0.262。

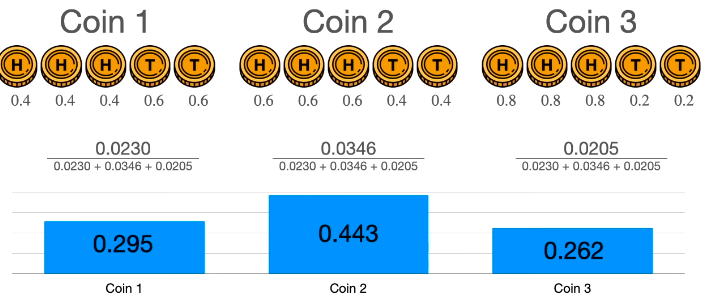
4

加到十个硬币 (每个硬币丢正的概率从 0, 0.1, 0.2 到 1)，任选一个丢 10 次，得到 7 正 3 反，最优可能是哪个硬币？

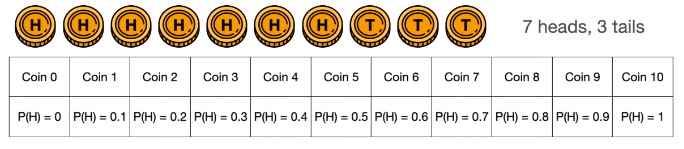
7 正 3 反，那么最有可能选到硬币 7 (丢正的概率为 0.7)。

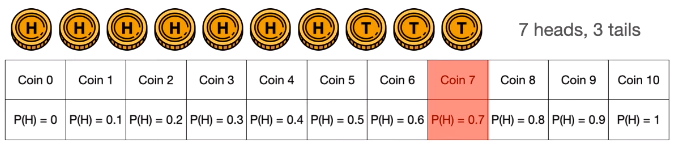
那么其他硬币的呢？也有可能选中，概率计算如下表。

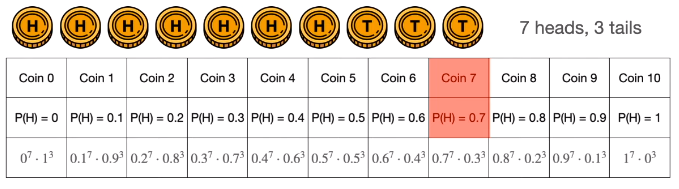
标准化 (除以十个概率的和) 得到下表的结果。

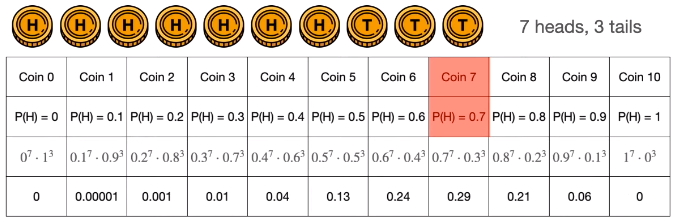
可视化如下。

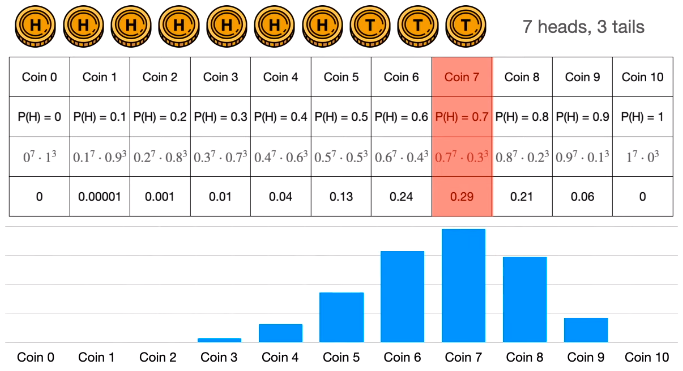
5

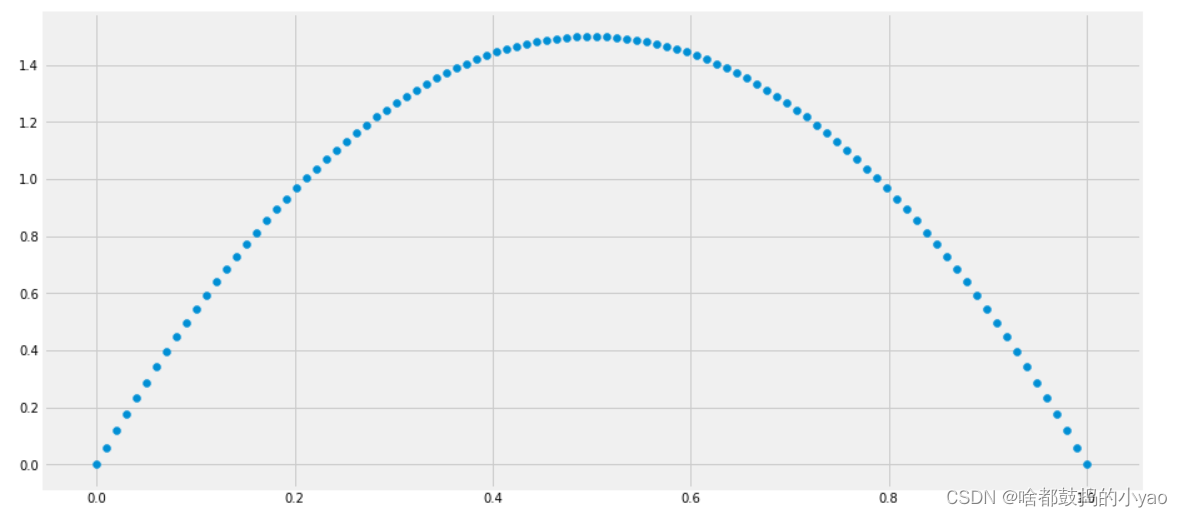
将上例的十个硬币 (丢正概率为 0 到 1) 扩展到无数个硬币 (丢正概率为 p)，那么任取一个硬币丢 10 次得到 7 正 3 反的概率为 p7 × (1-p)3。

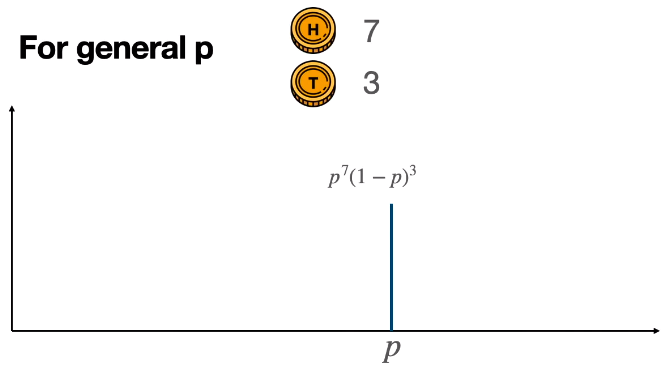
将 p 从 0 到 1 分隔很多点 p(i)，对每个 p(i) 计算出 p(i)7 × (1-p(i))3 并画出图。不难发现 p = 0.7 时函数值最高，即最有可能选取“丢正概率为 0.7”的硬币。

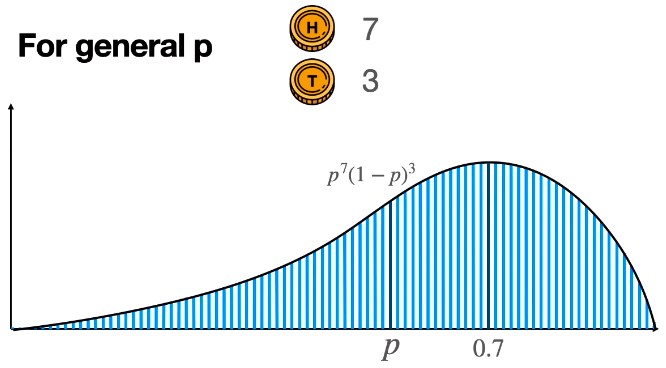
当选无限多个点 p(i) 时，就可完全填充曲线下的面积了。

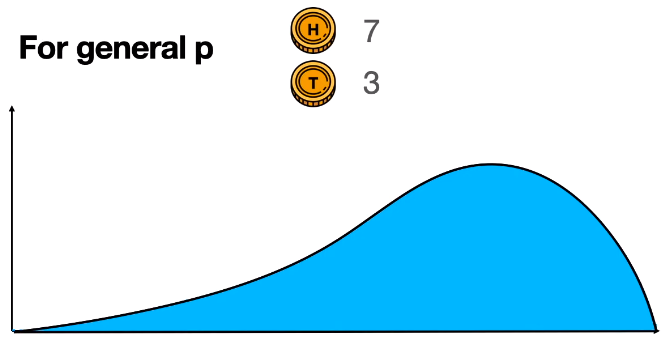
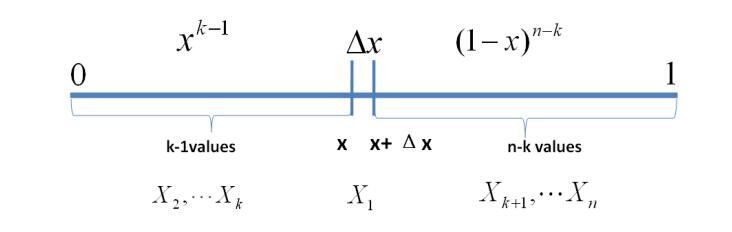
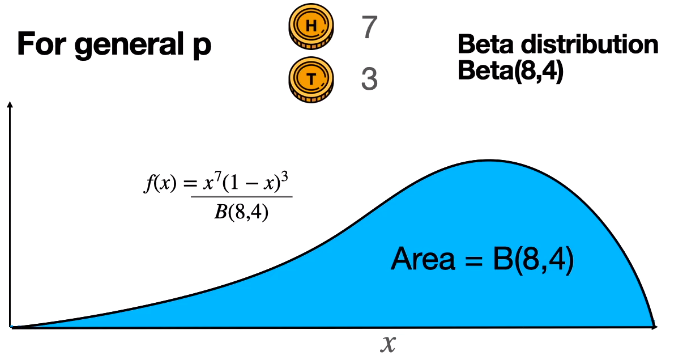
得到的概率值 x7 × (1-x)3 需要被标准化才能得到一个概率分布，而这个面积的大小，在本例中表示为 B(8, 4)，就是用来“标准化”概率除以的那个分母。

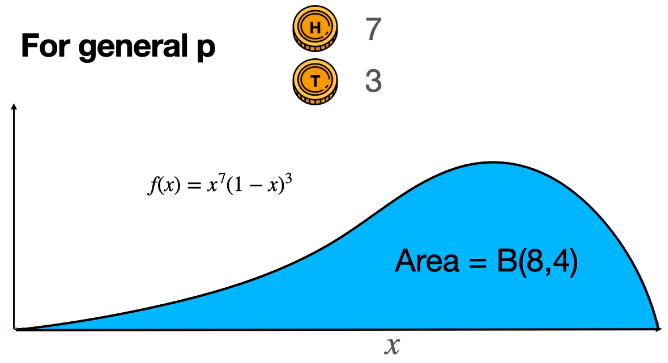
为什么表示为 B(8, 4) 而不是 B(7, 3)，这个是惯例，即在丢正的次数 7 和丢反的次数 3 加上 1，记住就行了。

6

这样  x7(1-x)3 / B(8, 4) 就构成了一个概率分布，即贝塔分布。

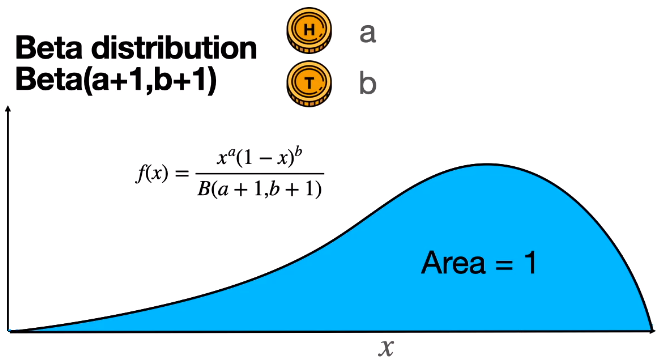
将具体“丢正的次数 7 和丢反的次数 3”分别用 a 和 b 表示，那么通用的贝塔分布的概率分布函数为 xa(1-x)b / B(a+1, b+1)。

7

现在假设观测到以下三种情况：

1. 7 正 3 反
   

2. 70 正 30 反

3. 700 正 300 反

很显然最有可能选取的硬币的丢正概率都为 0.7，但哪种情况最有信心来声称选取的硬币的丢正概率都为 0.7？

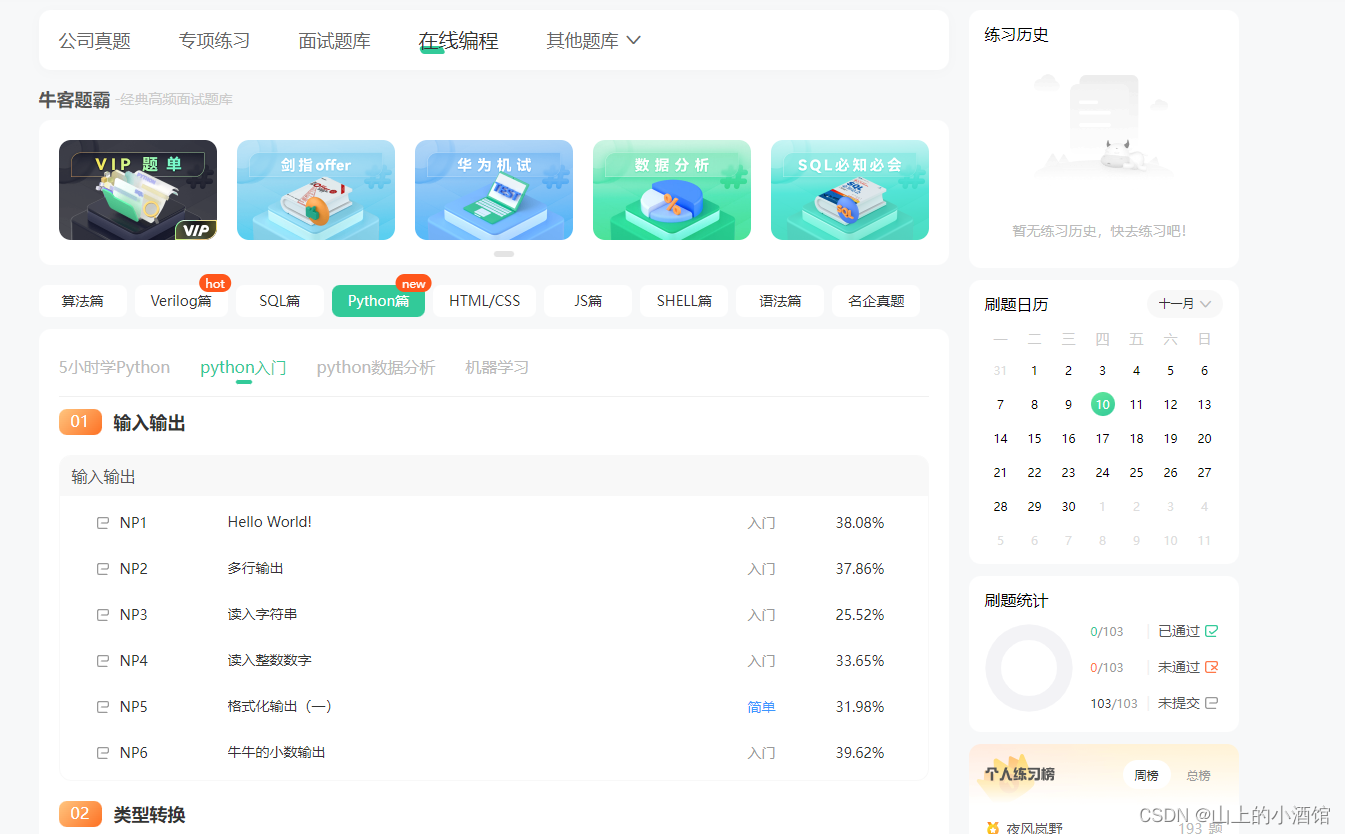
简单，将三种情况下的贝塔分布图画出即可。

三幅图相同的是，函数最大值都发生在 p = 0.7 时。

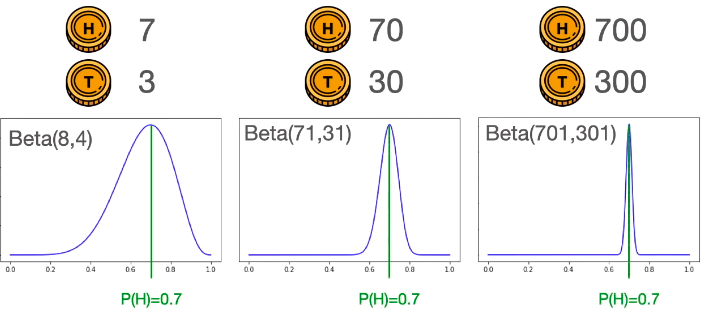
三幅图不同的是，从左到右来看，峰越来越尖，展开越来越窄，即越来越有信心声称选取的硬币的丢正概率为 0.7。

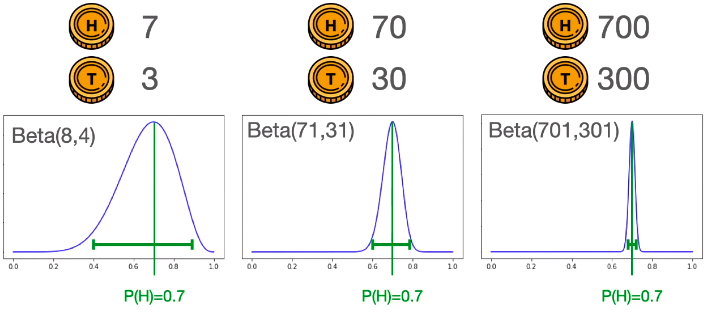
朋友们，你们弄懂了贝塔分布吗？

---

有兴趣学习 Python 和金融工程的同学，可以参考我自己做的精品课：

付费文章

Python 基础版 11 节目录

1. 编程概览

2. 元素型数据

3. 容器型数据

4. 流程控制：条件-循环-异常处理

5. 函数上：低阶函数

6. 函数下：高阶函数

7. 类和对象：封装-继承-多态-组合

8. 字符串专场：格式化和正则化

9. 解析表达式：简约也简单

10. 生成器和迭代器：简约不简单

11. 装饰器：高端不简单

数据分析进阶课的目录

1. NumPy 上

2. NumPy 下

3. Pandas 上

4. Pandas 下

5. SciPy 上

6. SciPy 下

7. Pandas 时间序列

8. Pandas 高频数据

9. 默顿模型 - 计量经济资本

10. LSMC - 美式百慕大期权定价

11. Bachelier - 负油价和负利率

12. Nelson Siegel - 债券收益率曲线构建
    

13. 外汇交易组合保证金

14. FR007 利率掉期定价和曲线拔靴

15. 量化交易 - 向量化回测
    

金融工程硬核付费文章

1. 欧式期权 PDE FD

2. 美式和百慕大期权 PDE FD

3. 单障碍和单触碰期权 PDE FD

4. 双障碍和双触碰期权 PDE FD

5. Snowball Autocallable PDE FD

6. 离散障碍和触碰期权 PDE FD