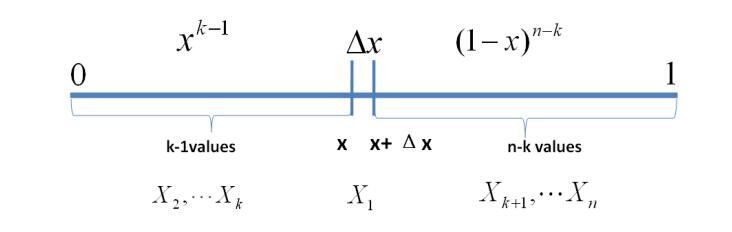
Beta 函数
B ( α , β ) ≜ ∫ 0 1 x α − 1 ( 1 − x ) β − 1 d x \Beta(\alpha, \beta) \triangleq \int_0^1 x^{\alpha-1}(1-x)^{\beta-1}dx B(α,β)≜∫01xα−1(1−x)β−1dx
其中 α , β > 0 \alpha, \beta > 0 α,β>0
Beta 函数与 Gamma 函数
B ( α , β ) = Γ ( α ) Γ ( β ) Γ ( α + β ) \Beta(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} B(α,β)=Γ(α+β)Γ(α)Γ(β)
当 α , β ∈ N + \alpha,\beta\in N^+ α,β∈N+ 时,
B ( α , β ) = ( α − 1 ) ! ( β − 1 ) ! ( α + β − 1 ) ! \Beta(\alpha, \beta) = \frac{(\alpha-1)!(\beta-1)!}{(\alpha+\beta-1)!} B(α,β)=(α+β−1)!(α−1)!(β−1)!
Beta 分布
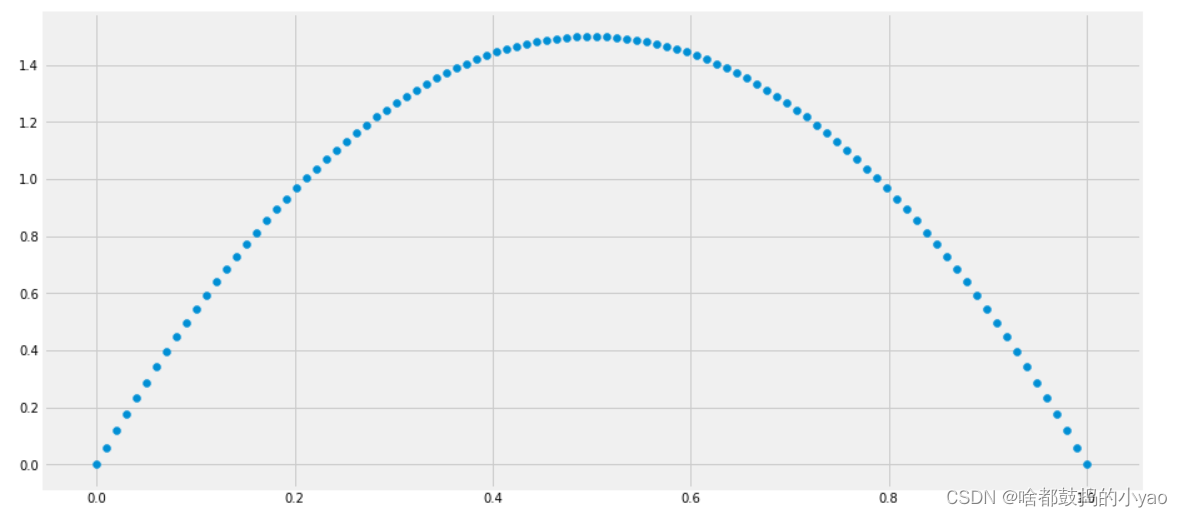
f ( x ; α , β ) ≜ 1 B ( α , β ) x α − 1 ( 1 − x ) β − 1 f(x;\alpha, \beta) \triangleq \frac{1}{\Beta(\alpha, \beta)} x^{\alpha-1}(1-x)^{\beta-1} f(x;α,β)≜B(α,β)1xα−1(1−x)β−1
为定义在 [ 0 , 1 ] [0,1] [0,1]上的 Beta分布 的概率密度函数,显然
∫ 0 1 f ( x ; α , β ) d x = 1 \int_0^1 f(x;\alpha, \beta) dx = 1 ∫01f(x;α,β)dx=1
Beta 分布的期望
∫ 0 1 x f ( x ; α , β ) d x = ∫ 0 1 1 B ( α , β ) x α ( 1 − x ) β − 1 d x = 1 B ( α , β ) ∫ 0 1 x α + 1 − 1 ( 1 − x ) β − 1 d x = B ( α + 1 , β ) B ( α , β ) = Γ ( α + 1 ) Γ ( β ) Γ ( α + 1 + β ) Γ ( α + β ) Γ ( α ) Γ ( β ) = α α + β \begin{aligned} \int_0^1 xf(x;\alpha, \beta) dx &=\int_0^1 \frac{1}{\Beta(\alpha, \beta)} x^{\alpha}(1-x)^{\beta-1}dx \\\\ &=\frac{1}{\Beta(\alpha, \beta)} \int_0^1 x^{\alpha+1-1}(1-x)^{\beta-1}dx \\\\ &=\frac{\Beta(\alpha+1, \beta)}{\Beta(\alpha, \beta)} \\\\ &= \frac{\Gamma(\alpha+1)\Gamma(\beta)}{\Gamma(\alpha+1+\beta)}\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} \\\\ &= \frac{\alpha}{\alpha+\beta} \end{aligned} ∫01xf(x;α,β)dx=∫01B(α,β)1xα(1−x)β−1dx=B(α,β)1∫01xα+1−1(1−x)β−1dx=B(α,β)B(α+1,β)=Γ(α+1+β)Γ(α+1)Γ(β)Γ(α)Γ(β)Γ(α+β)=α+βα
Beta-Binomial 共轭
假定二项分布 B ( n , p ) B(n, p) B(n,p) 的参数 p p p 服从 B e t a ( p ; α , β ) Beta(p;\alpha,\beta) Beta(p;α,β) 先验分布
p ∼ B e t a ( p ; α , β ) = 1 B ( α , β ) p α − 1 ( 1 − p ) β − 1 p \sim Beta(p;\alpha,\beta) = \frac{1}{\Beta(\alpha, \beta)} p^{\alpha-1}(1-p)^{\beta-1} p∼Beta(p;α,β)=B(α,β)1pα−1(1−p)β−1
然后又做了 n 1 + n 2 n_1 + n_2 n1+n2 次伯努利实验(记为 W W W),成功 n 1 n_1 n1 次,失败 n 2 n_2 n2 次,于是后验分布为
P ( p ∣ W ) = P ( p , W ) P ( W ) = P ( W ∣ p ) P ( p ) ∫ 0 1 P ( W ∣ p ) P ( p ) d p = ( n 1 + n 2 n 1 ) p n 1 ( 1 − p ) n 2 1 B ( α , β ) p α − 1 ( 1 − p ) β − 1 ∫ 0 1 ( n 1 + n 2 n 1 ) p n 1 ( 1 − p ) n 2 1 B ( α , β ) p α − 1 ( 1 − p ) β − 1 d p = p n 1 + α − 1 ( 1 − p ) n 2 + β − 1 ∫ 0 1 p n 1 + α − 1 ( 1 − p ) n 2 + β − 1 d p = p n 1 + α − 1 ( 1 − p ) n 2 + β − 1 B ( n 1 + α , n 2 + β ) \begin{aligned} P(p|W) &= \frac{P(p,W)}{P(W)} \\\\ &= \frac{P(W|p)P(p)}{\int_0^1P(W|p)P(p)dp} \\\\ &= \frac{\dbinom{n_1+n_2}{n_1}p^{n_1}(1-p)^{n_2} \frac{1}{\Beta(\alpha, \beta)} p^{\alpha-1}(1-p)^{\beta-1}}{\int_0^1\dbinom{n_1+n_2}{n_1}p^{n_1}(1-p)^{n_2}\frac{1}{\Beta(\alpha, \beta)} p^{\alpha-1}(1-p)^{\beta-1}dp} \\\\ &= \frac{ p^{n_1+\alpha-1}(1-p)^{n_2+\beta-1}}{\int_0^1 p^{n_1+\alpha-1}(1-p)^{n_2+\beta-1}dp} \\\\ &= \frac{ p^{n_1+\alpha-1}(1-p)^{n_2+\beta-1}}{\Beta(n_1+\alpha, n_2 + \beta)} \\\\ \end{aligned} P(p∣W)=P(W)P(p,W)=∫01P(W∣p)P(p)dpP(W∣p)P(p)=∫01(n1n1+n2)pn1(1−p)n2B(α,β)1pα−1(1−p)β−1dp(n1n1+n2)pn1(1−p)n2B(α,β)1pα−1(1−p)β−1=∫01pn1+α−1(1−p)n2+β−1dppn1+α−1(1−p)n2+β−1=B(n1+α,n2+β)pn1+α−1(1−p)n2+β−1即服从 B e t a ( n 1 + α , n 2 + β ) Beta(n_1+\alpha, n_2 + \beta) Beta(n1+α,n2+β) 分布!
简而言之:
B e t a ( α , β ) + B i n o m C o u n t ( n 1 , n 2 ) = B e t a ( n 1 + α , n 2 + β ) Beta(\alpha, \beta) + BinomCount(n_1, n_2) = Beta(n_1+\alpha, n_2 + \beta) Beta(α,β)+BinomCount(n1,n2)=Beta(n1+α,n2+β)

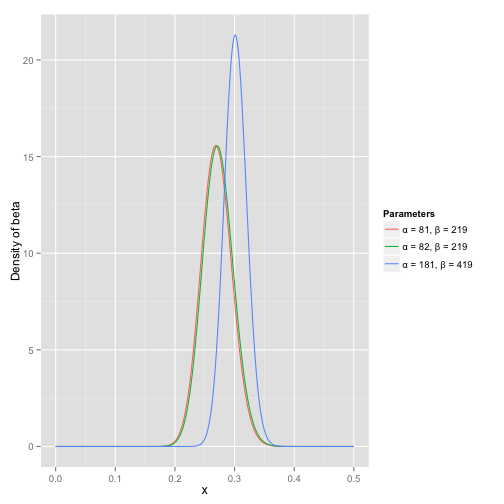
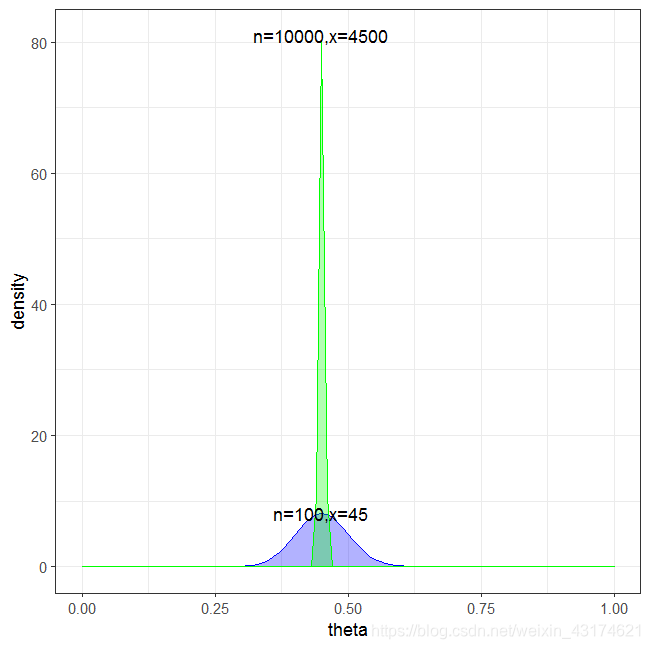
Beta 分布是二项分布的共轭先验, α \alpha α 和 β \beta β 可以分别看成伯努利试验中成功和失败的次数,而 B e t a ( p ; α , β ) Beta(p;\alpha, \beta) Beta(p;α,β)就是对伯努利试验中成功概率 p p p 的概率密度函数。
上图中的蓝色虚线对应 p = 0.25 p = 0.25 p=0.25,是 Beta(2,6) 和 Beta(10,30) 的期望值,即:
0.25 = 2 2 + 6 = 10 10 + 30 0.25 = \frac{2}{2+6} = \frac{10}{10+30} 0.25=2+62=10+3010
但是可以明显看出 Beta(10,30) 的概率密度曲线要比 Beta(2,6)更尖锐,说明当实验次数越多时,对 p = 0.25 p = 0.25 p=0.25 的信念越强!