#beta分布介绍
相信大家学过统计学的都对 正态分布 二项分布 均匀分布 等等很熟悉了,但是却鲜少有人去介绍beta分布的。
用一句话来说,beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可能性大小。
举一个简单的例子,熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average),就是用一个运动员击中的球数除以击球的总数,我们一般认为0.266是正常水平的击球率,而如果击球率高达0.3就被认为是非常优秀的。
现在有一个棒球运动员,我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率,用击中的数除以击球数,但是如果这个棒球运动员只打了一次,而且还命中了,那么他就击球率就是100%了,这显然是不合理的,因为根据棒球的历史信息,我们知道这个击球率应该是0.215到0.36之间才对啊。
对于这个问题,我们可以用一个二项分布表示(一系列成功或失败),一个最好的方法来表示这些经验(在统计中称为先验信息)就是用beta分布,这表示在我们没有看到这个运动员打球之前,我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。
接下来我们将这些先验信息转换为beta分布的参数,我们知道一个击球率应该是平均0.27左右,而他的范围是0.21到0.35,那么根据这个信息,我们可以取 α = 81 , β = 219 \alpha=81 ,\beta=219 α=81,β=219

之所以取这两个参数是因为:
- beta分布的均值是 α α + β = 81 81 + 219 = 0.27 \frac{\alpha}{\alpha+\beta}=\frac{81}{81+219}=0.27 α+βα=81+21981=0.27
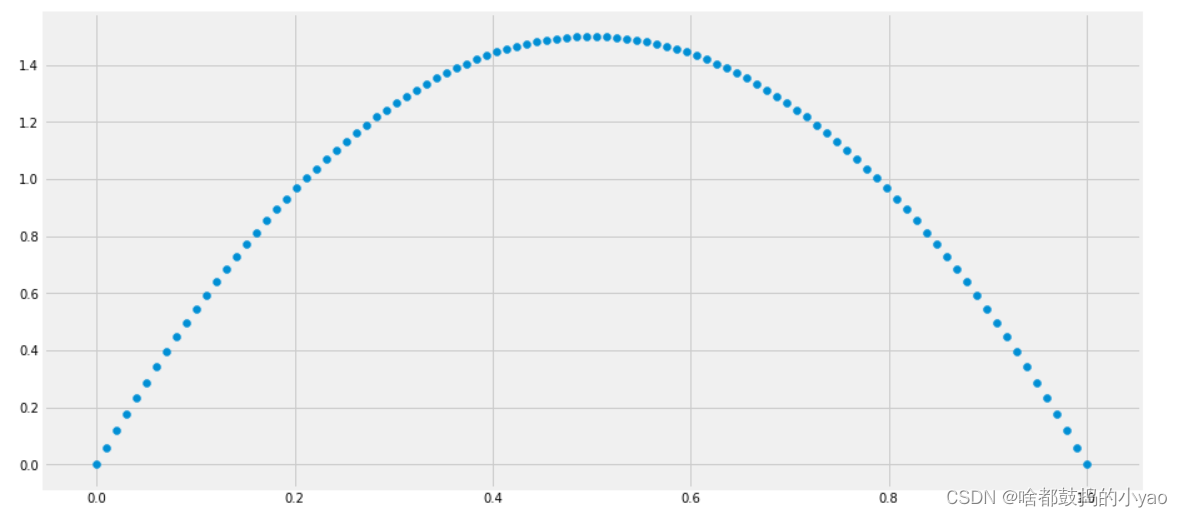
- 从图中可以看到这个分布主要落在了(0.2,0.35)间,这是从经验中得出的合理的范围。
在这个例子里,我们的x轴就表示各个击球率的取值,x对应的y值就是这个击球率所对应的概率。也就是说beta分布可以看作一个概率的概率分布。
那么有了先验信息后,现在我们考虑一个运动员只打一次球,那么他现在的数据就是"1中;1击"。这时候我们就可以更新我们的分布了,让这个曲线做一些移动去适应我们的新信息。beta分布在数学上就给我们提供了这一性质,他与二项分布是共轭先验的(Conjugate_prior)。所谓共轭先验就是先验分布是beta分布,而后验分布同样是beta分布。结果很简单:
B e t a ( α 0 + h i t s , β 0 + m i s s e s ) Beta(\alpha_0+hits, \beta_0+misses) Beta(α0+hits,β0+misses)
其中 α 0 \alpha_0 α0和 β 0 \beta_0 β0是一开始的参数,在这里是81和219。所以在这一例子里, α \alpha α增加了1(击中了一次)。 β \beta β没有增加(没有漏球)。这就是我们的新的beta分布 B e t a ( 81 + 1 , 219 ) Beta(81+1, 219) Beta(81+1,219),我们跟原来的比较一下:

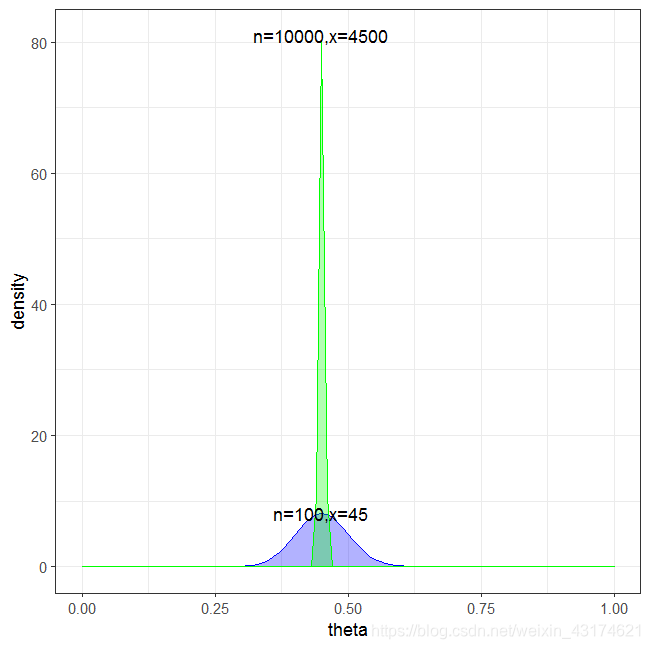
可以看到这个分布其实没多大变化,这是因为只打了1次球并不能说明什么问题。但是如果我们得到了更多的数据,假设一共打了300次,其中击中了100次,200次没击中,那么这一新分布就是:
B e t a ( 81 + 100 , 219 + 200 ) Beta(81+100, 219+200) Beta(81+100,219+200)

注意到这个曲线变得更加尖,并且平移到了一个右边的位置,表示比平均水平要高。
一个有趣的事情是,根据这个新的beta分布,我们可以得出他的数学期望为: α α + β = 82 + 100 82 + 100 + 219 + 200 = . 303 \frac{\alpha}{\alpha+\beta}=\frac{82+100}{82+100+219+200}=.303 α+βα=82+100+219+20082+100=.303 ,这一结果要比直接的估计要小 100 100 + 200 = . 333 \frac{100}{100+200}=.333 100+200100=.333 。你可能已经意识到,我们事实上就是在这个运动员在击球之前可以理解为他已经成功了81次,失败了219次这样一个先验信息。
因此,对于一个我们不知道概率是什么,而又有一些合理的猜测时,beta分布能很好的作为一个表示概率的概率分布。
#beta分布与二项分布的共轭先验性质
##二项分布
二项分布即重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项分布服从0-1分布
二项分布的似然函数:
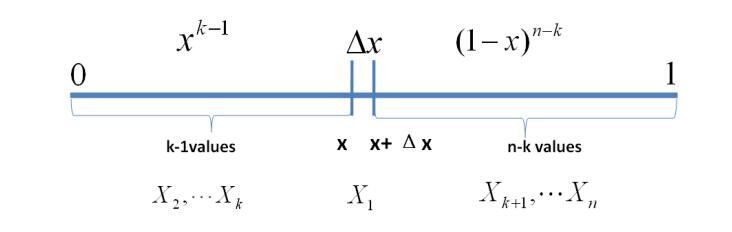
P ( d a t a ∣ θ ) ∝ θ z ( 1 − θ ) N − z z = ∑ i = 1 N X i P(data|\theta) \propto \theta^z(1-\theta)^{N-z} \\ z=\sum_{i=1}^NX_i P(data∣θ)∝θz(1−θ)N−zz=i=1∑NXi
##beta分布
B e t a ( a , b ) = θ a − 1 ( 1 − θ ) b − 1 B ( a , b ) ∝ θ a − 1 ( 1 − θ ) b − 1 Beta(a,b)=\frac{\theta^{a-1}(1-\theta)^{b-1}}{B(a,b)}\propto \theta^{a-1}(1-\theta)^{b-1} Beta(a,b)=B(a,b)θa−1(1−θ)b−1∝θa−1(1−θ)b−1
在beta分布中,B函数是一个标准化函数,它只是为了使得这个分布的概率密度积分等于1才加上的。
##贝叶斯估计
我们做贝叶斯估计的目的就是要在给定数据的情况下求出 θ \theta θ的值,所以我们的目的是求解如下后验概率:
P ( θ ∣ d a t a ) = P ( d a t a ∣ θ ) P ( θ ) P ( d a t a ) ∝ P ( d a t a ∣ θ ) P ( θ ) P(\theta |data)=\frac{P(data|\theta)P(\theta)}{P(data)}\propto P(data|\theta)P(\theta) P(θ∣data)=P(data)P(data∣θ)P(θ)∝P(data∣θ)P(θ)
注意到因为P(data)与我们所需要估计的 θ \theta θ是独立的,因此我们可以不考虑它。
我们称 P ( d a t a ∣ θ ) P(data|\theta) P(data∣θ)为似然函数, P ( θ ) P(\theta) P(θ)为先验分布
##共轭先验
现在我们有了二项分布的似然函数和beta分布,现在我们将beta分布代进贝叶斯估计中的 P ( θ ) P(\theta) P(θ)中,将二项分布的似然函数代入 P ( d a t a ∣ θ ) P(data|\theta) P(data∣θ)中,可以得到:
P ( θ ∣ d a t a ) ∝ θ z ( 1 − θ ) N − z ∗ θ a − 1 ( 1 − θ ) b − 1 ∝ θ a + z − 1 ( 1 − θ ) b + N − z − 1 P(\theta |data) \propto \theta^z(1-\theta)^{N-z}*\theta^{a-1}(1-\theta)^{b-1} \\ \propto \theta^{a+z-1}(1-\theta)^{b+N-z-1} P(θ∣data)∝θz(1−θ)N−z∗θa−1(1−θ)b−1∝θa+z−1(1−θ)b+N−z−1
我们设 a ′ = a + z , b ′ = b + N − z a'=a+z,b'=b+N-z a′=a+z,b′=b+N−z
最后我们发现这个贝叶斯估计服从Beta(a’,b’)分布的,我们只要用B函数将它标准化就得到我们的后验概率:
P ( θ ∣ d a t a ) = θ a ′ − 1 ( 1 − θ ) b ′ − 1 B ( a ′ , b ′ ) P(\theta |data)=\frac{\theta^{a'-1}(1-\theta)^{b'-1}}{B(a',b')} P(θ∣data)=B(a′,b′)θa′−1(1−θ)b′−1
#参考资料:
1.Understanding the beta distribution (using baseball statistics)
2.20 - Beta conjugate prior to Binomial and Bernoulli likelihoods
作为分享主义者(sharism),本人所有互联网发布的图文均遵从CC版权,转载请保留作者信息并注明作者a358463121专栏:http://blog.csdn.net/a358463121,如果涉及源代码请注明GitHub地址:https://github.com/358463121/。商业使用请联系作者。