定义：

beta分布可以看作一个概率的概率分布，当你不知道一个东西的具体概率是多少时，它可以给出了所有概率出现的可能性大小。

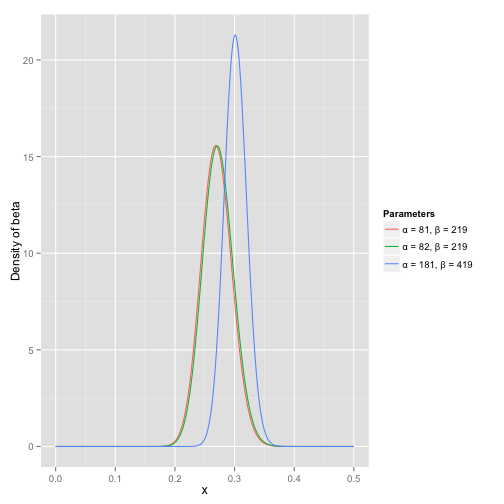
举一个简单的例子，熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average)，就是用一个运动员击中的球数除以击球的总数，我们一般认为0.266是正常水平的击球率，而如果击球率高达0.3就被认为是非常优秀的。现在有一个棒球运动员，我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率，用击中的数除以击球数，但是如果这个棒球运动员只打了一次，而且还命中了，那么他就击球率就是100%了，这显然是不合理的，因为根据棒球的历史信息，我们知道这个击球率应该是0.215到0.36之间才对啊。对于这个问题一个最好的方法就是用beta分布，这表示在我们没有看到这个运动员打球之前，我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。接下来我们将这些先验信息转换为beta分布的参数，我们知道一个击球率应该是平均0.27左右，而他的范围是0.21到0.35，那么根据这个信息，我们可以取α=81,β=219（击中了81次，未击中219次）

之所以取这两个参数是因为：

• beta分布的均值是从图中可以看到这个分布主要落在了(0.2,0.35)间，这是从经验中得出的合理的范围。
• 在这个例子里，我们的x轴就表示各个击球率的取值，x对应的y值就是这个击球率所对应的概率。也就是说beta分布可以看作一个概率的概率分布。

         

 公式： 

# IMPORTS
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import matplotlib.style as style
from IPython.core.display import HTML# PLOTTING CONFIG
%matplotlib inline
style.use('fivethirtyeight')
plt.rcParams["figure.figsize"] = (14, 7)plt.figure(dpi=100)# PDF
plt.plot(np.linspace(0, 1, 100), stats.beta.pdf(np.linspace(0, 1, 100),a=2,b=2) )
print (stats.beta.pdf(np.linspace(0, 1, 100),a=2,b=2))
plt.fill_between(np.linspace(0, 1, 100),stats.beta.pdf(np.linspace(0, 1, 100),a=2,b=2),alpha=.15)# CDF
plt.plot(np.linspace(0, 1, 100), stats.beta.cdf(np.linspace(0, 1, 100),a=2,b=2),)# LEGEND
plt.text(x=0.1, y=.7, s="pdf (normed)", rotation=52, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=0.45, y=.5, s="cdf", rotation=40, alpha=.75, weight="bold", color="#fc4f30")# TICKS
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)# TITLE, SUBTITLE & FOOTER
plt.text(x = -.125, y = 1.85, s = "Beta Distribution - Overview",fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -.125, y = 1.6, s = 'Depicted below are the normed probability density function (pdf) and the cumulative density\nfunction (cdf) of a beta distributed random variable ' + r'$ y \sim Beta(\alpha, \beta)$, given $ \alpha = 2 $ and $ \beta = 2$.',fontsize = 19, alpha = .85)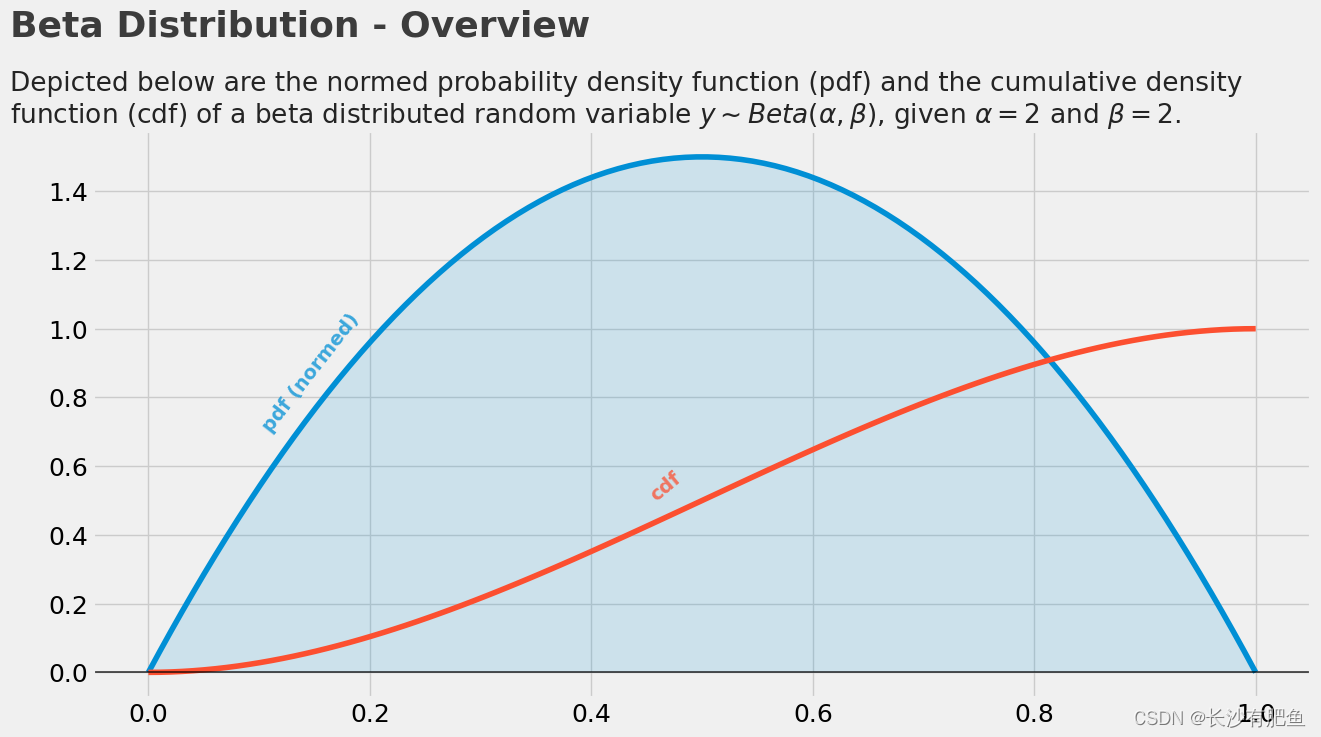

 改变参数α和β对结果产生的影响如下所示：

plt.figure(dpi=100)# A = B = 1
plt.plot(np.linspace(0, 1, 200), stats.beta.pdf(np.linspace(0, 1, 200), a=1, b=1),)
plt.fill_between(np.linspace(0, 1, 200),stats.beta.pdf(np.linspace(0, 1, 200), a=1, b=1),alpha=.15,)# A = B = 10
plt.plot(np.linspace(0, 1, 200), stats.beta.pdf(np.linspace(0, 1, 200), a=10, b=10),)
plt.fill_between(np.linspace(0, 1, 200),stats.beta.pdf(np.linspace(0, 1, 200), a=10, b=10),alpha=.15,)# A = B = 100
plt.plot(np.linspace(0, 1, 200), stats.beta.pdf(np.linspace(0, 1, 200), a=100, b=100),)
plt.fill_between(np.linspace(0, 1, 200),stats.beta.pdf(np.linspace(0, 1, 200), a=100, b=100),alpha=.15,)# LEGEND
plt.text(x=0.1, y=1.45, s=r"$ \alpha = 1, \beta = 1$", alpha=.75, weight="bold", color="#008fd5")
plt.text(x=0.325, y=3.5, s=r"$ \alpha = 10, \beta = 10$", rotation=35, alpha=.75, weight="bold", color="#fc4f30")
plt.text(x=0.4125, y=8, s=r"$ \alpha = 100, \beta = 100$", rotation=80, alpha=.75, weight="bold", color="#e5ae38")# TICKS
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)# TITLE, SUBTITLE & FOOTER
plt.text(x = -.1, y = 13.75, s = r"Beta Distribution - constant $\frac{\alpha}{\beta}$, varying $\alpha + \beta$",fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -.1, y = 12, s = 'Depicted below are three beta distributed random variables with '+ r'equal $\frac{\alpha}{\beta} $ and varying $\alpha+\beta$'+'.\nAs one can see the sum of ' + r'$\alpha + \beta$ (mainly) sharpens the distribution (the bigger the sharper).',fontsize = 19, alpha = .85)

 

plt.figure(dpi=100)# A / B = 1/3
plt.plot(np.linspace(0, 1, 200), stats.beta.pdf(np.linspace(0, 1, 200), a=25, b=75),)
plt.fill_between(np.linspace(0, 1, 200),stats.beta.pdf(np.linspace(0, 1, 200), a=25, b=75),alpha=.15,)# A / B = 1
plt.plot(np.linspace(0, 1, 200), stats.beta.pdf(np.linspace(0, 1, 200), a=50, b=50),)
plt.fill_between(np.linspace(0, 1, 200),stats.beta.pdf(np.linspace(0, 1, 200), a=50, b=50),alpha=.15,)# A / B = 3
plt.plot(np.linspace(0, 1, 200), stats.beta.pdf(np.linspace(0, 1, 200), a=75, b=25),)
plt.fill_between(np.linspace(0, 1, 200),stats.beta.pdf(np.linspace(0, 1, 200), a=75, b=25),alpha=.15,)# LEGEND
plt.text(x=0.15, y=5, s=r"$ \alpha = 25, \beta = 75$", rotation=80, alpha=.75, weight="bold", color="#008fd5")
plt.text(x=0.39, y=5, s=r"$ \alpha = 50, \beta = 50$", rotation=80, alpha=.75, weight="bold", color="#fc4f30")
plt.text(x=0.65, y=5, s=r"$ \alpha = 75, \beta = 25$", rotation=80, alpha=.75, weight="bold", color="#e5ae38")# TICKS
plt.tick_params(axis = 'both', which = 'major', labelsize = 18)
plt.axhline(y = 0, color = 'black', linewidth = 1.3, alpha = .7)# TITLE, SUBTITLE & FOOTER
plt.text(x = -.1, y = 11.75, s = r"Beta Distribution - constant $\alpha + \beta$, varying $\frac{\alpha}{\beta}$",fontsize = 26, weight = 'bold', alpha = .75)
plt.text(x = -.1, y = 10, s = 'Depicted below are three beta distributed random variables with '+ r'equal $\alpha+\beta$ and varying $\frac{\alpha}{\beta} $'+'.\nAs one can see the fraction of ' + r'$\frac{\alpha}{\beta} $ (mainly) shifts the distribution ' + r'($\alpha$ towards 1, $\beta$ towards 0).',fontsize = 19, alpha = .85)

 构造随机beta分布：

from scipy.stats import beta# draw a single sample
print(beta.rvs(a=2, b=2), end="\n\n")# draw 10 samples
print(beta.rvs(a=2, b=2, size=10))

0.736118736802914[0.52821195 0.41843068 0.64285567 0.13075973 0.47871566 0.720698170.27643923 0.38471512 0.51838499 0.64945068]

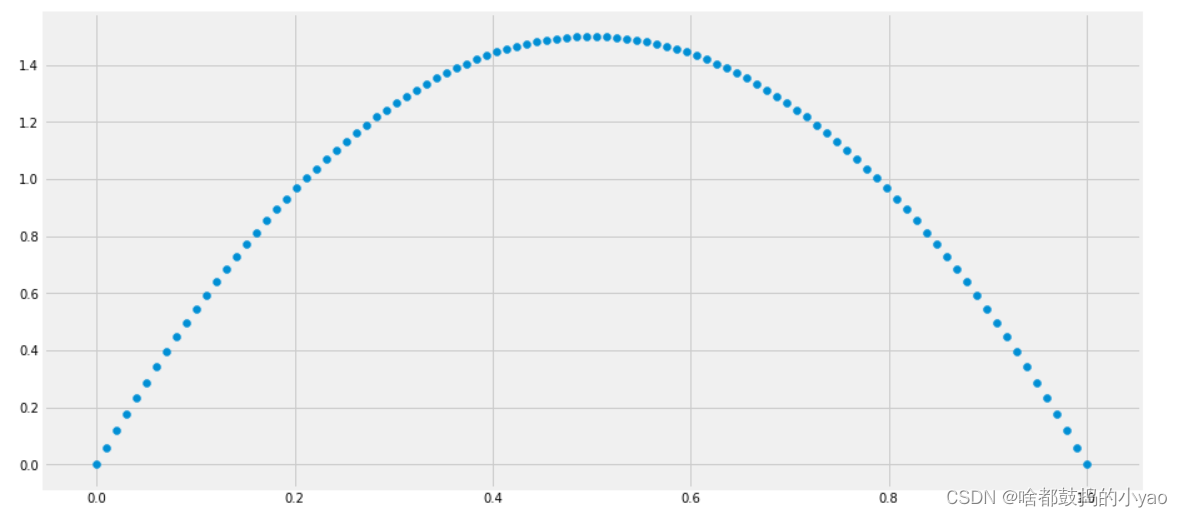
 概率密度函数：

from scipy.stats import beta# additional import for plotting
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams["figure.figsize"] = (14, 7)# continuous pdf for the plot
x_s = np.linspace(0, 1, 100)
y_s = beta.pdf(a=2, b=2, x=x_s)
plt.scatter(x_s, y_s);

 累计概率密度函数：

from scipy.stats import beta# probability of x less or equal 0.3
print("P(X <0.3) = {:.3}".format(beta.cdf(a=2, b=2, x=0.3)))# probability of x in [-0.2, +0.2]
print("P(-0.2 < X < 0.2) = {:.3}".format(beta.cdf(a=2, b=2, x=0.2) - beta.cdf(a=2, b=2, x=-0.2)))

P(X <0.3) = 0.216
P(-0.2 < X < 0.2) = 0.104