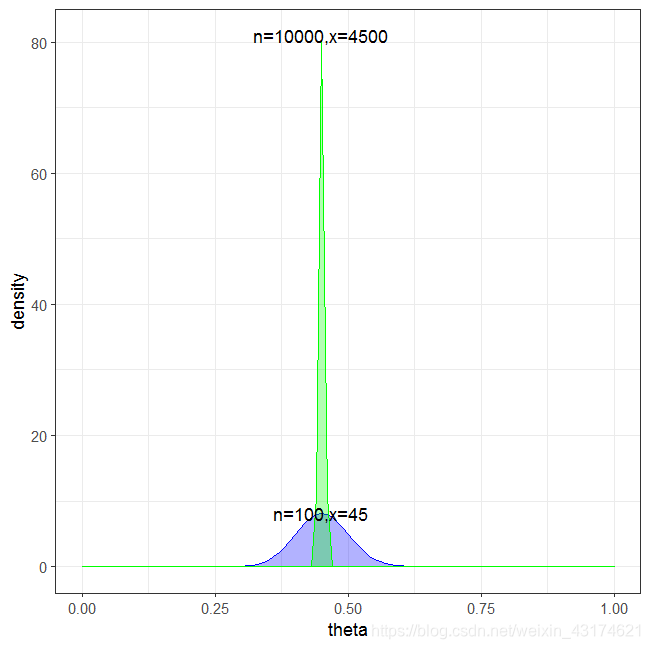
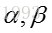相信大家学过统计学的都对 正态分布 二项分布 均匀分布 等等很熟悉了,但是却鲜少有人去介绍beta分布的。
用一句话来说,beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可能性大小。
举一个简单的例子,熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average),就是用一个运动员击中的球数除以击球的总数,我们一般认为0.266是正常水平的击球率,而如果击球率高达0.3就被认为是非常优秀的。
现在有一个棒球运动员,我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率,用击中的数除以击球数,但是如果这个棒球运动员只打了一次,而且还命中了,那么他就击球率就是100%了,这显然是不合理的,因为根据棒球的历史信息,我们知道这个击球率应该是0.215到0.36之间才对啊。
对于这个问题,我们可以用一个二项分布表示(一系列成功或失败),一个最好的方法来表示这些经验(在统计中称为先验信息)就是用beta分布,这表示在我们没有看到这个运动员打球之前,我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。
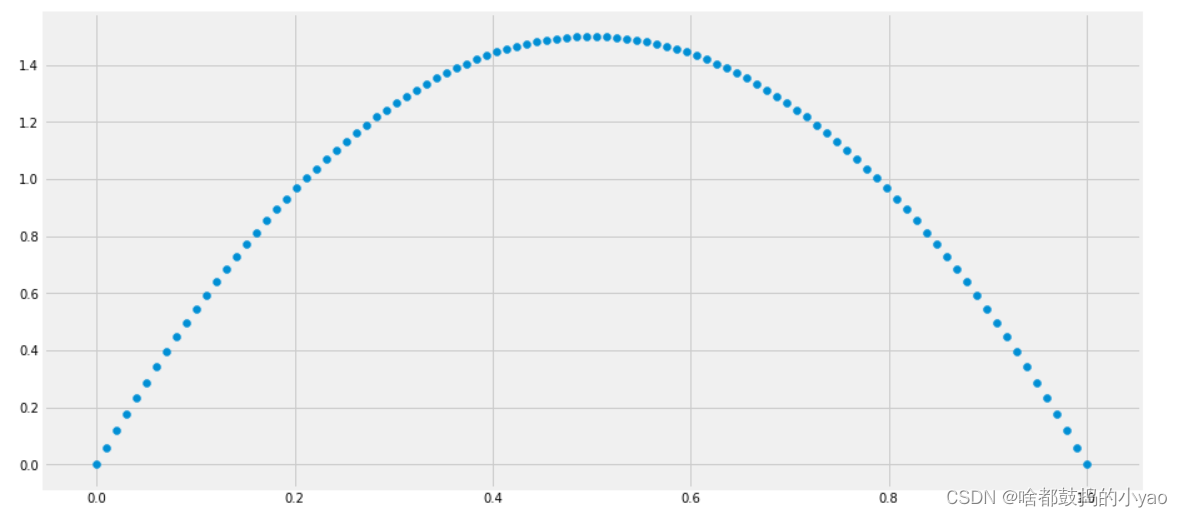
接下来我们将这些先验信息转换为beta分布的参数,我们知道一个击球率应该是平均0.27左右,而他的范围是0.21到0.35,那么根据这个信息,我们可以取α=81,β=219。
之所以取这两个参数是因为:
1、beta分布的均值是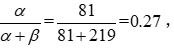
2、从图中可以看到这个分布主要落在了(0.2,0.35)间,这是从经验中得出的合理的范围。

在这个例子里,我们的x轴就表示各个击球率的取值,x对应的y值就是这个击球率所对应的概率。也就是说beta分布可以看作一个概率的概率分布。
那么有了先验信息后,现在我们考虑一个运动员只打一次球,那么他现在的数据就是”1中;1击”。这时候我们就可以更新我们的分布了,让这个曲线做一些移动去适应我们的新信息。beta分布在数学上就给我们提供了这一性质,他与二项分布是共轭先验的(Conjugate_prior)。所谓共轭先验就是先验分布是beta分布,而后验分布同样是beta分布。结果很简单:


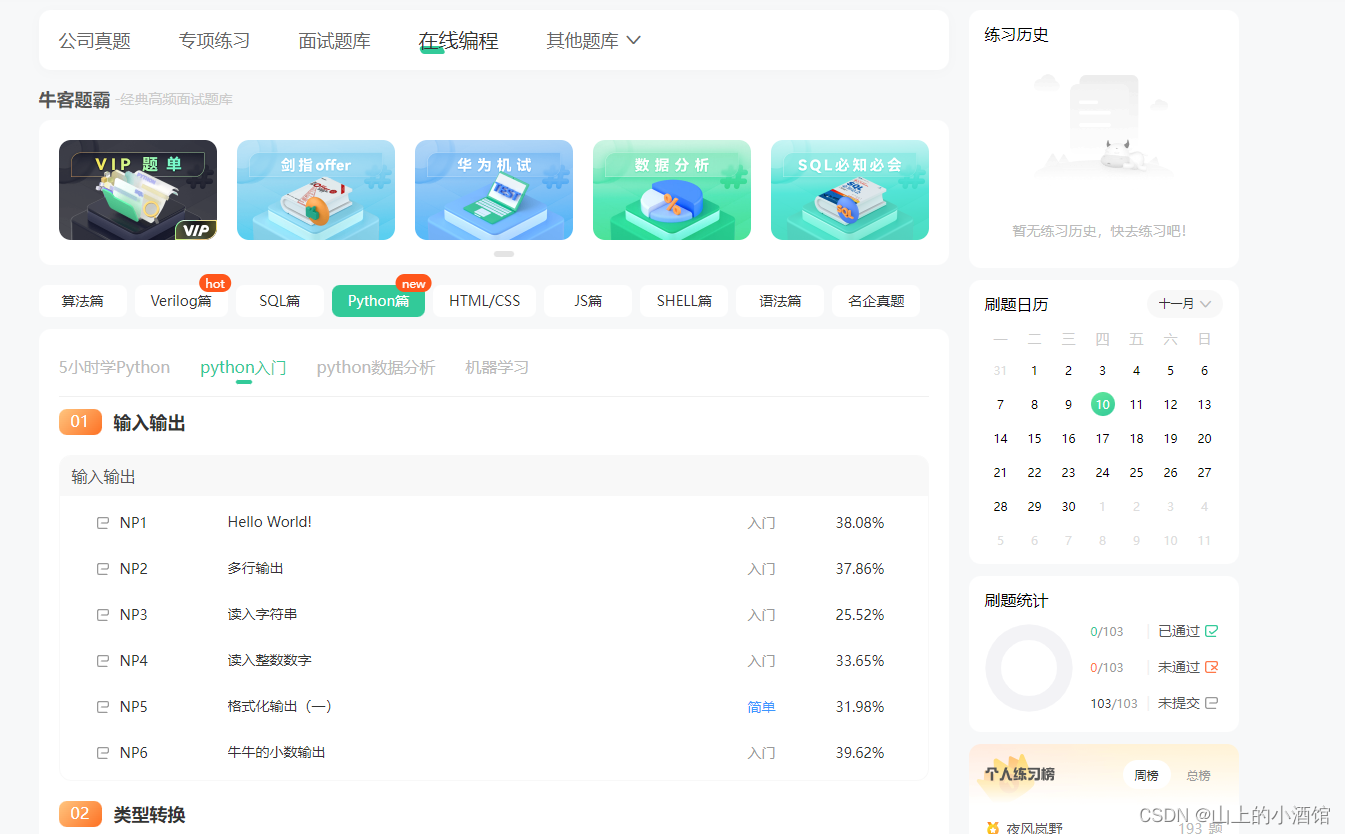
可以看到这个分布其实没多大变化,这是因为只打了1次球并不能说明什么问题。但是如果我们得到了更多的数据,假设一共打了300次,其中击中了100次,200次没击中,那么这一新分布就是:
beta(81+100,219+200)


参考:http://blog.csdn.net/a358463121/article/details/52562940
beta分布介绍
article/2025/10/15 15:57:23
相关文章
泊松过程、伽马分布、贝塔分布及狄利克雷分布
泊松过程、伽马分布、贝塔分布及狄利克雷分布 1.泊松过程1.1Poisson过程的定义1.2Poisson过程的应用 2.伽马分布2.1伽马分布的定义2.2伽马分布的性质2.3伽马分布与其他分布的关系 3.贝塔分布3.1贝塔分布的定义3.2贝塔分布的图形3.3贝塔分布的应用 4.狄利克雷分布4.1狄利克雷分布…
贝叶斯分析——分布之分布(beta分布)
转自:http://blog.sciencenet.cn/blog-677221-1049350.html
贝叶斯与逆概率问题
对于“白球黑球”的概率问题。概率问题可以正向计算,也能反推回去。
(1)盒子里有10个球,黑白两种颜色,如果我们知道10个球中5白5黑&a…
Beta分布(Beta Distribution)
定义:
beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可能性大小。
举一个简单的例子,熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average),就是…
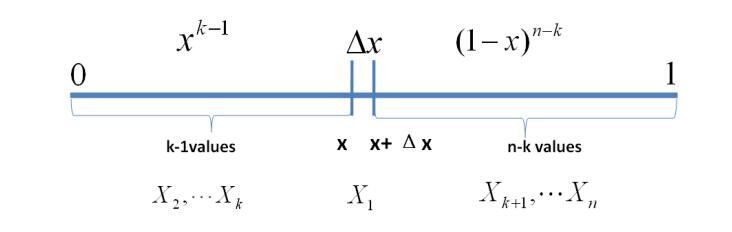
推导Beta分布公式
Beta分布可以用于拟合各种不同的分布,网上各种资料对于Beta分布的原理着墨较多,却少有推导Beta分布公式的,所以,推导Beta分布公式如下: 设一组随机变量 ,将这n个随机变量排序后得到顺序统计量 ,…
如何理解beta分布?
相信大家学过统计学的都对 正态分布 二项分布 均匀分布 等等很熟悉了,但是却鲜少有人去介绍beta分布的。
用一句话来说,beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可…
原创 | 一文读懂正态分布与贝塔分布
本文约2300字,建议阅读5分钟 本文通过案例介绍了正态分布和贝塔分布的概念。 正态分布 正态分布,是一种非常常见的连续概率分布,其也叫做常态分布(normal distribution),或者根据其前期的研究贡献者之一高斯的名字来称…
带你理解beta分布
#beta分布介绍 相信大家学过统计学的都对 正态分布 二项分布 均匀分布 等等很熟悉了,但是却鲜少有人去介绍beta分布的。
用一句话来说,beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所…
深入理解什么是Beta分布
例一
Beta分布是一种描述概率的概率分布,这句话可能有些绕口,看一个例子:
以抛硬币为例,如果硬币是均匀的,并且正面朝上的概率记为p(p0.5),那么每一次抛硬币都可以看做是一次伯努利…
贝塔分布(beta分布)及Python实现——计算机视觉修炼之路(二)
beta分布
贝塔分布( Beta Distribution ) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数,在机器学习和数理统计学中有重要应用。在概率论中,贝塔分布,是指一组定义在(0,1)区间的连续概率分布。其概率密度函数为&…
Beta分布(概率的概率)
目录 1.前言
2.定义 3.Beat分布的概率密度函数(PDF):
4.Beat分布的累积密度函数(CDF): 1.前言
伯努利试验(同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验…
伽马分布与 贝塔分布
伽马函数
称 为伽马函数,其中参数 ,伽马函数具有如下性质: ,n为自然数;或写作
余元公式:对于 ,有
与贝塔函数 的关系 : 对于 ;伽马函数是严格凹函数。x足够大时,可以用Stirling 公式来计算Gam…
数据科学分布——Beta分布
Beta分布 概念参数影响数量比例 随机产生数据概率密度函数累积概率密度函数 概念
贝塔分布(Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数,在机器学习和数理统计学中有重要应用。在概率论中,贝塔分布&#…
Beta分布及其应用
贝塔分布(Beta Distribution)是一个连续的概率分布,它只有两个参数。它最重要的应用是为某项实验的成功概率建模。在本篇博客中,我们使用Beta分布作为描述。
原文地址:http://www.datalearner.com/blog/1051505532393…
机器学习中的数学——常用概率分布(十):贝塔分布(Beta分布)
分类目录:《机器学习中的数学》总目录 相关文章: 常用概率分布(一):伯努利分布(Bernoulli分布) 常用概率分布(二):范畴分布(Multinoulli分布&am…
NLPIR分词系统的使用
前身是2000年发布的ICTCLAS,2009年更为现名。张华平博士打造。
Java课设做自动问答系统,用到了,所以记录一下使用方法,网上方法可能有点老,所以自己发现没有那么复杂。
https://github.com/NLPIR-team/NLPIR 上下载源…
中科院分词ICTCLAS汉语分词系统简单配置
汉语分词一直来说都是进行文本分析的瓶颈,这里介绍一个汉语分词系统ICTCLAS,全球很受欢迎的汉语分词开源系统,曾获得首界国际分词大赛综合排名第一,国家973评测第一名;支持词典,多级词性标注,支…