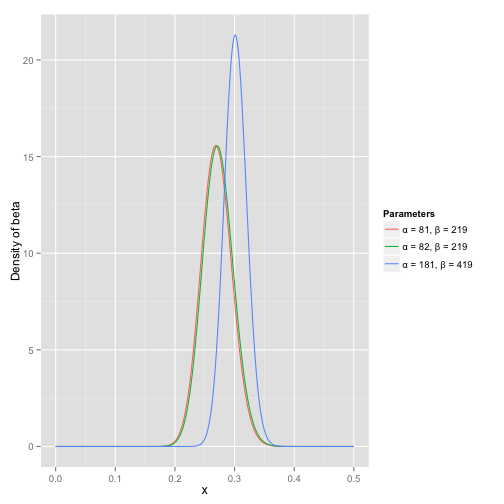
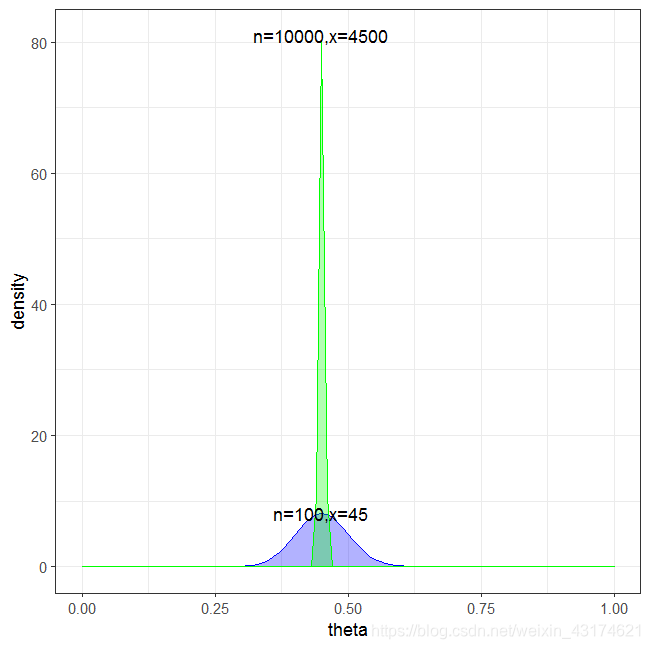
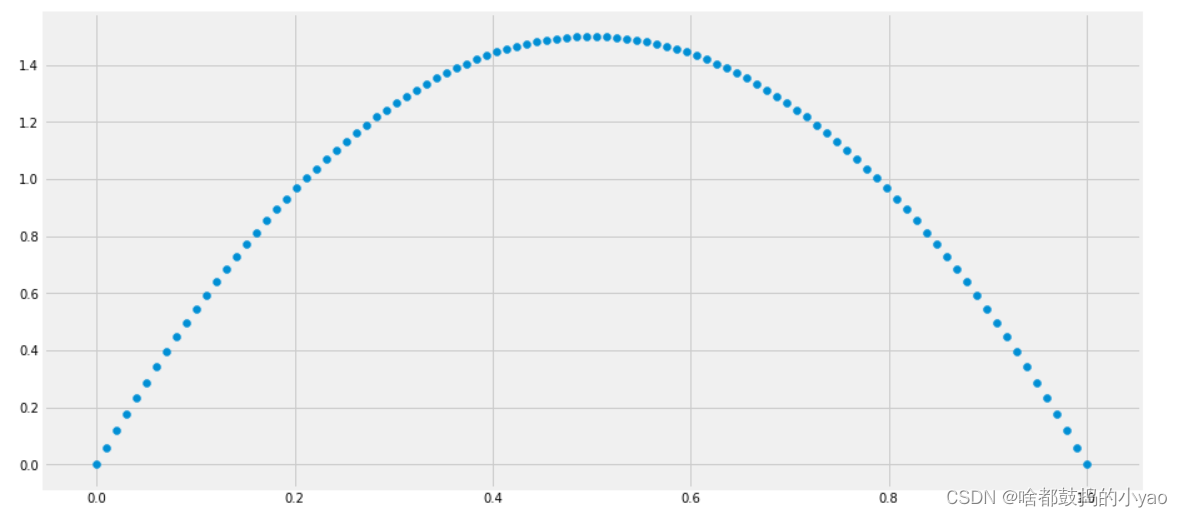
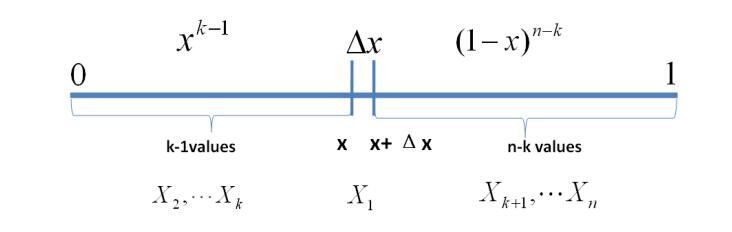
Beta分布可以用于拟合各种不同的分布,网上各种资料对于Beta分布的原理着墨较多,却少有推导Beta分布公式的,所以,推导Beta分布公式如下:
设一组随机变量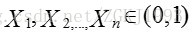
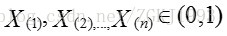
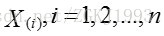
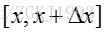
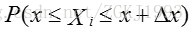
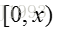
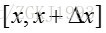
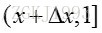
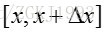
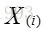
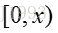
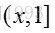
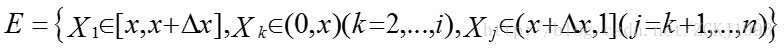
则有:
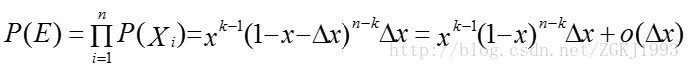
考虑较为复杂的情形,假设n个数中有两个数落在了区间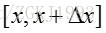
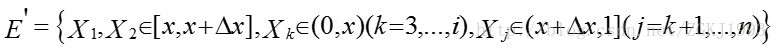
则有:
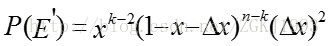
从以上分析可以看出,只要落在 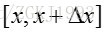
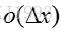
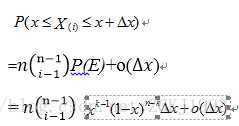
所以,可以得到 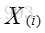
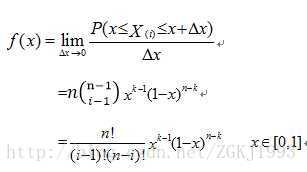
利用Gamma函数,可以把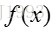
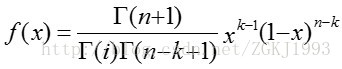
取 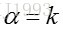
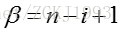
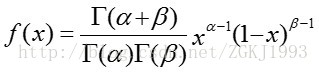
此即为标准Beta分布的概率密度函数。更为一般的 分布概率密度函数为:
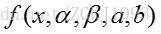
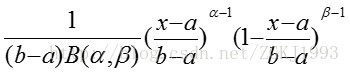
式中:
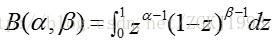
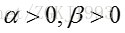
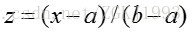
称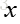
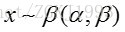
形状参数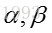
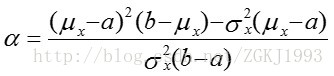
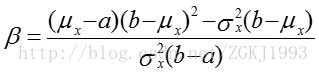
式中, 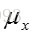
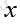
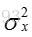
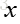
通过 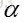
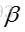
得到一组样本数据后,通过调整eta分布的形状参数 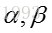
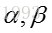
推导Beta分布公式
article/2025/10/15 16:41:31
相关文章
如何理解beta分布?
相信大家学过统计学的都对 正态分布 二项分布 均匀分布 等等很熟悉了,但是却鲜少有人去介绍beta分布的。
用一句话来说,beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所有概率出现的可…
原创 | 一文读懂正态分布与贝塔分布
本文约2300字,建议阅读5分钟 本文通过案例介绍了正态分布和贝塔分布的概念。 正态分布 正态分布,是一种非常常见的连续概率分布,其也叫做常态分布(normal distribution),或者根据其前期的研究贡献者之一高斯的名字来称…
带你理解beta分布
#beta分布介绍 相信大家学过统计学的都对 正态分布 二项分布 均匀分布 等等很熟悉了,但是却鲜少有人去介绍beta分布的。
用一句话来说,beta分布可以看作一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出了所…
深入理解什么是Beta分布
例一
Beta分布是一种描述概率的概率分布,这句话可能有些绕口,看一个例子:
以抛硬币为例,如果硬币是均匀的,并且正面朝上的概率记为p(p0.5),那么每一次抛硬币都可以看做是一次伯努利…
贝塔分布(beta分布)及Python实现——计算机视觉修炼之路(二)
beta分布
贝塔分布( Beta Distribution ) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数,在机器学习和数理统计学中有重要应用。在概率论中,贝塔分布,是指一组定义在(0,1)区间的连续概率分布。其概率密度函数为&…
Beta分布(概率的概率)
目录 1.前言
2.定义 3.Beat分布的概率密度函数(PDF):
4.Beat分布的累积密度函数(CDF): 1.前言
伯努利试验(同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验…
伽马分布与 贝塔分布
伽马函数
称 为伽马函数,其中参数 ,伽马函数具有如下性质: ,n为自然数;或写作
余元公式:对于 ,有
与贝塔函数 的关系 : 对于 ;伽马函数是严格凹函数。x足够大时,可以用Stirling 公式来计算Gam…
数据科学分布——Beta分布
Beta分布 概念参数影响数量比例 随机产生数据概率密度函数累积概率密度函数 概念
贝塔分布(Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数,在机器学习和数理统计学中有重要应用。在概率论中,贝塔分布&#…
Beta分布及其应用
贝塔分布(Beta Distribution)是一个连续的概率分布,它只有两个参数。它最重要的应用是为某项实验的成功概率建模。在本篇博客中,我们使用Beta分布作为描述。
原文地址:http://www.datalearner.com/blog/1051505532393…
机器学习中的数学——常用概率分布(十):贝塔分布(Beta分布)
分类目录:《机器学习中的数学》总目录 相关文章: 常用概率分布(一):伯努利分布(Bernoulli分布) 常用概率分布(二):范畴分布(Multinoulli分布&am…
NLPIR分词系统的使用
前身是2000年发布的ICTCLAS,2009年更为现名。张华平博士打造。
Java课设做自动问答系统,用到了,所以记录一下使用方法,网上方法可能有点老,所以自己发现没有那么复杂。
https://github.com/NLPIR-team/NLPIR 上下载源…
中科院分词ICTCLAS汉语分词系统简单配置
汉语分词一直来说都是进行文本分析的瓶颈,这里介绍一个汉语分词系统ICTCLAS,全球很受欢迎的汉语分词开源系统,曾获得首界国际分词大赛综合排名第一,国家973评测第一名;支持词典,多级词性标注,支…
智能语言-中科院分词系统ICTCLAS(NLPIR)
智能语言的处理中,第一个步骤就是分词。一个句子处理的第一步就是分词了,目前而言中文分词中效果最好的就是中科院分词系统。在2014版本以及之前称为ICTCLAS,之后的版本都更名为NLPIR。 我给出一个最简单的使用教程,能够帮助新手…
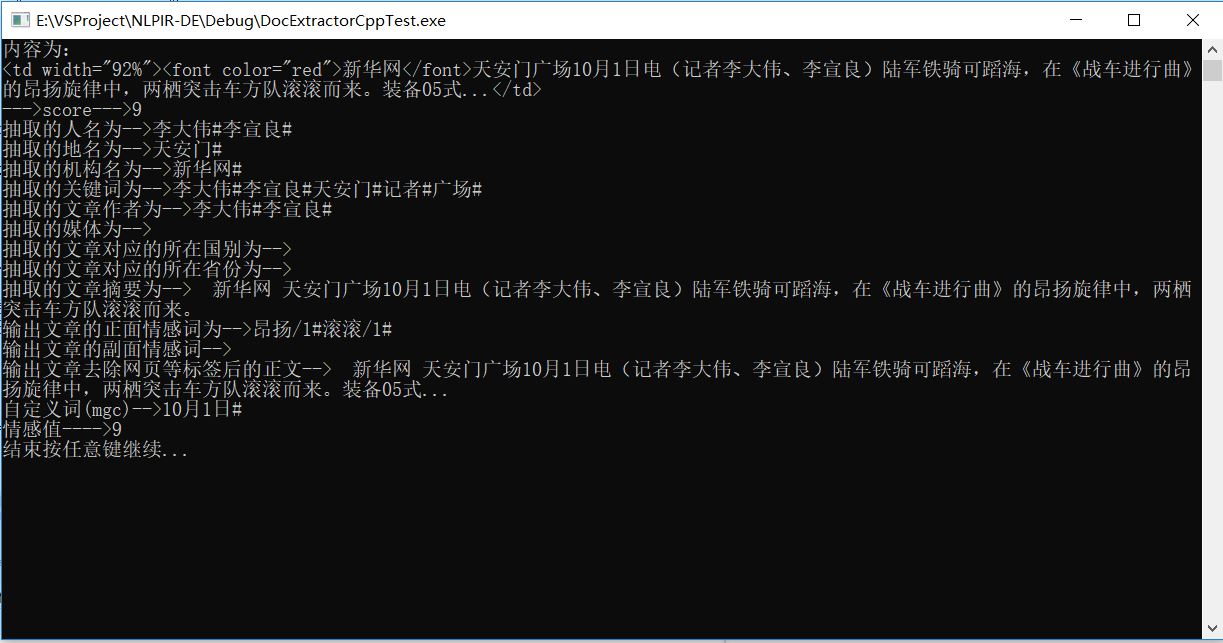
NLPIR(北理工张华平版中文分词系统)的SDK(C++)调用方法
一、本文内容简介
关于中文分词的基本概念关于NLPIR(北理工张华平版中文分词系统)的基本情况具体SDK模块(C版)的组装方法
二、具体内容
1. 中文分词的基本概念 中文分词是自然语言处理的一个分支,自然语言即人们在日常生活中使用的语言,包含书面语,口…
哈工大中文分词系统LTP(pyltp)学习笔记
一、LTP简介 介绍:语言技术平台(LTP) 提供包括中文分词、词性标注、命名实体识别、依存句法分析、语义角色标注等丰富、高效、精准的自然语言处理技术。经过 哈工大社会计算与信息检索研究中心 11 年的持续研发和推广,LTP已经成为国内外最具影响力的中文…
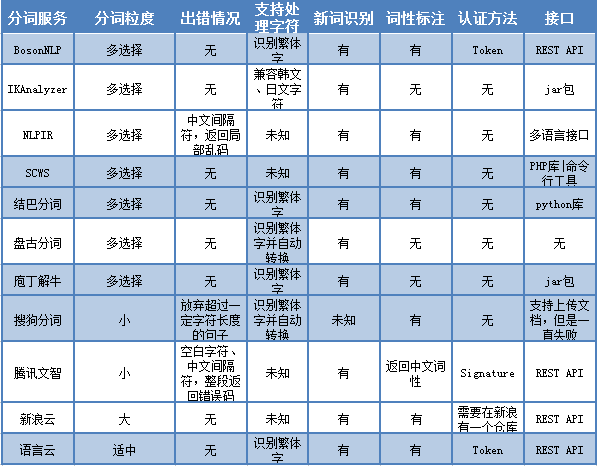
比较热门好用的开源中文分词软件系统有哪些?
在逐渐步入DT(Data Technology)时代的今天,自然语义分析技术越发不可或缺。对于我们每天打交道的中文来说,并没有类似英文空格的边界标志。而理解句子所包含的词语,则是理解汉语语句的第一步。汉语自动分词的任务&…