本文约2300字,建议阅读5分钟
本文通过案例介绍了正态分布和贝塔分布的概念。
正态分布
正态分布,是一种非常常见的连续概率分布,其也叫做常态分布(normal distribution),或者根据其前期的研究贡献者之一高斯的名字来称呼,高斯分布(Gaussian distribution)。正态分布是自然科学与行为科学中的定量现象的一个方便模型。
各种各样的心理学测试结果和物理现象的观测值,比如光子计数等都被发现近似地服从正态分布。甚至生活中很多现象的表征结果也符合正态分布的分布规律。尽管这些现象的根本原因经常是未知的,甚至被采样的样本的原始群体分布并不服从正态分布,但这个变量的采样分布均值仍会近似服从正态分布。
正态分布的概率密度函数呈左右对称的钟形,其具体表达式为:
因为正态分布是如此的常见而这个式子是如此的奇怪,我们打算重温高斯当年的推导过程,但部分细节不会那么严谨的证明,只是带领大家看看高斯当年的思路是如何的。
首先,高斯事先假定了如下条件,才得到了正态分布的连续密度函数。
即: 误差分布导出的极大似然估计 = 算术平均值
这里我们把全部过程用直白的语言复述一遍。
设某物理量真值为 , 而这里我们由于误差等原因,没办法测量得到真值,所以只能对 进行一系列的观测,打算从这些观测值来推断真值。设 为n次独立的观测测量值。站在上帝视角,我们知道每次测量的误差为 ,假设误差 的概率密度函数为 , 如果我们有办法求得 的一般形式,就求得了正态分布(实际上是观测误差的概率分布)的密度分布函数。所以我们的最终目的就是求 的解析表达式。
这些测量值们的联合概率为 个误差的联合概率,记为
我们应该让 取最大值。为求极大似然估计,令
整理后可以得到
别忘了,我们是要从上面的式子想办法求 。令 ,
由于高斯假设真值 在极大似然下就等于算术平均值 ,把解代入上式,可以得到
(1)式中取 , 有
由于此时有 , 并且 是任意都可能取到的,由此得到
因此 是一个奇函数。
(1)式中再取 , 并且要求 , 则有 , 并且
所以得到
注意到这里 是任意实数。
我们换一种角度来看,就是
这也是个大名鼎鼎的方程,叫做柯西函数方程。容易证明在有理数范围内可以得到唯一连续通解,当然也容易证明(这个真不太容易)在实数域内也有相同形式的唯一通解。
这个解就是
我们知道 , 从而进一步可以求解出
由于 是概率密度函数, 在所有实数域内积分为1,且大于0。因此这里我们把 换成 。结合这些边界条件,可以进一步得到
所以我们得到了
至此,测量误差分布的概率密度函数推导结束。
贝塔分布
贝塔分布,beta分布,简单来说,就是一个事件出现的概率的概率密度分布。
举个例子,篮球比赛的三分命中率是衡量篮球后卫运动员很重要的一个指标。通过过去的历史经验,我们知道运动员的三分命中率很难超过40%。假如老张是一个优秀老练的篮球后卫,其过去历史的三分命中率是35%,总投数为10000次,命中次为3500次。请问他在新赛季刚开始的时候,得到了一次三分投球机会,请问他这次投中的概率服从什么分布呢?
我们必须清楚,这个概率一定不是确定的,而是服从某种分布。这个概率密度分布函数应该在0.35处最大,沿两边逐渐递减。
这个概率就服从beta分布。确切的说,是服从
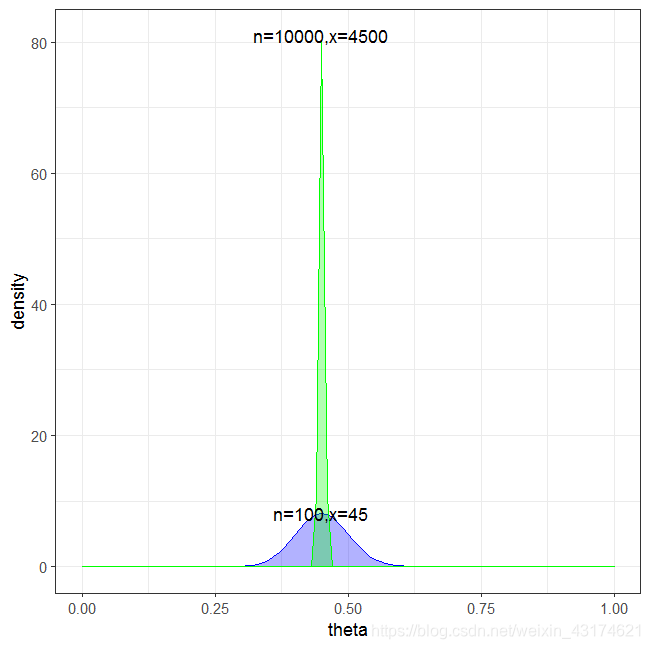
还有个运动员小张,而小张很年轻也很优秀,他的历史三分命中率也是35%,但是总投数为1000次,命中次数为350次。请问他在新赛季首投三分,命中概率的分布和老张一样吗?
明显不一样!虽然他们的历史投球命中率都是35%,但是我们直觉认为老张比小张更靠谱,老张首投命中的概率密度分布应该在0.35附近高于小张的。事实上,我们可以迅速借助python的scipy库中内置的beta统计方法。
from scipy import statsimport matplotlib.pyplot as pltimport numpy as np
x = np.linspace(0,0.7,1000)plt.plot(x,stats.beta.pdf(x,a=350,b=650),c='b',label='350/1000')plt.plot(x,stats.beta.pdf(x,a=3500,b=6500),c='g',label='3500/10000')plt.legend()plt.show()
我们来看一下图像。
的确如此。那么beta分布的具体表达式是什么呢?
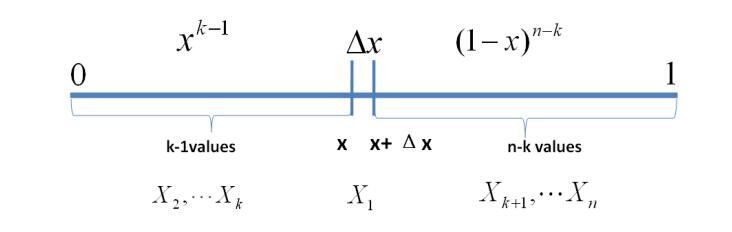
beta分布的表达式有两个参数 ,
公式是:
写成这样的式子很好理解,就是分子(命中 次且没命中 次的概率)除以分母(出现命中 次且没命中 次所有命中率出现的概率总和)。
而结合伽马函数 和贝塔函数,这种写法可以进一步简化:
关于伽马函数和贝塔函数,这里我们不做赘述。
需要指出的是,看起来beta分布的概率密度函数和高斯分布的曲线很像,实则不然。
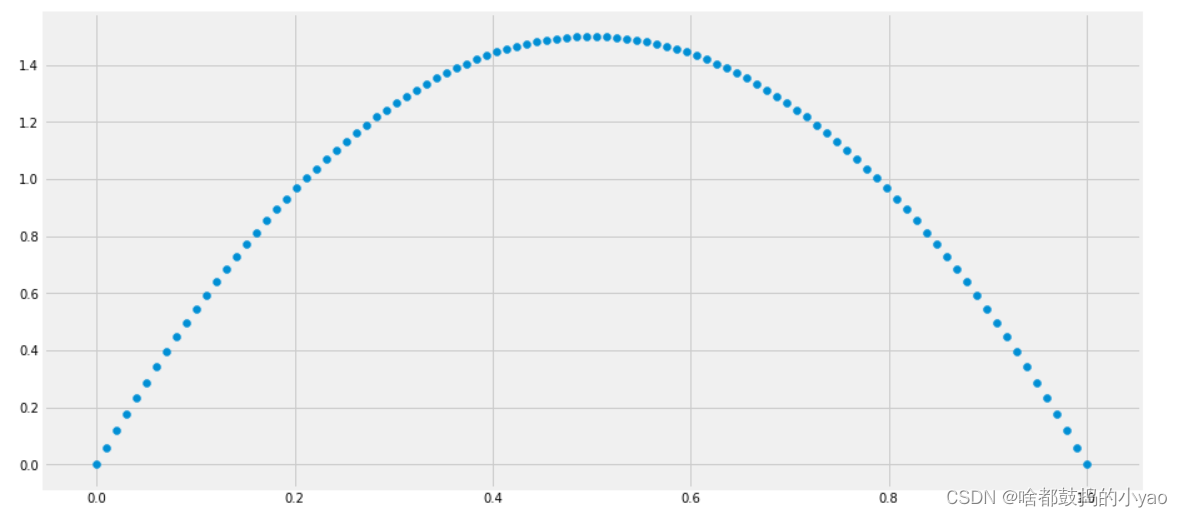
再举个例子,假如老张的孙子也想做做运动员,老张煞有介事的统计了小小张的历史三分投数,为5投1中。问他下一次投球,也就是第六次投球,命中的概率的分布是怎样的?如果过去是5投2中,5投3中,和5投4中呢?
可以看到,beta分布的PDF和高斯分布的曲线形状差别可大了。
作者:贾恩东
编辑:王菁
校对:林亦霖
数据派研究部介绍
数据派研究部成立于2017年初,以兴趣为核心划分多个组别,各组既遵循研究部整体的知识分享和实践项目规划,又各具特色:
算法模型组:积极组队参加kaggle等比赛,原创手把手教系列文章;
调研分析组:通过专访等方式调研大数据的应用,探索数据产品之美;
系统平台组:追踪大数据&人工智能系统平台技术前沿,对话专家;
自然语言处理组:重于实践,积极参加比赛及策划各类文本分析项目;
制造业大数据组:秉工业强国之梦,产学研政结合,挖掘数据价值;
数据可视化组:将信息与艺术融合,探索数据之美,学用可视化讲故事;
网络爬虫组:爬取网络信息,配合其他各组开发创意项目。
点击文末“阅读原文”,报名数据派研究部志愿者,总有一组适合你~
转载须知
如需转载,请在开篇显著位置注明作者和出处(转自:数据派THUID:DatapiTHU),并在文章结尾放置数据派醒目二维码。有原创标识文章,请发送【文章名称-待授权公众号名称及ID】至联系邮箱,申请白名单授权并按要求编辑。
未经许可的转载以及改编者,我们将依法追究其法律责任。
点击“阅读原文”加入组织~