1 类的加载机制

类的加载指的是将类的.class文件中的二进制数据读入到内存中，将其放在运行时数据区的方法区内，然后在堆区创建一个java.lang.Class对象，用来封装类在方法区内的数据结构。类的加载的最终产品是位于堆区中的Class对象，Class对象封装了类在方法区内的数据结构，并且向Java程序员提供了访问方法区内的数据结构的接口。

1.1 类的加载过程

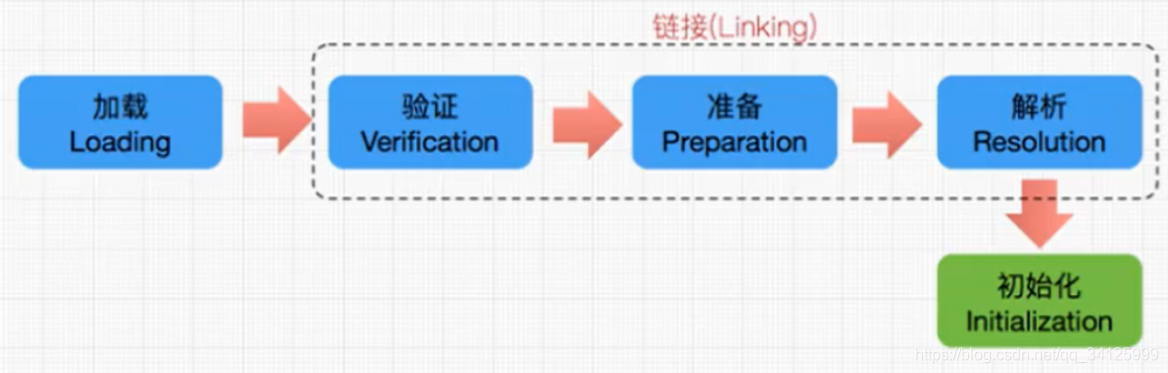
1.2 加载

所谓加载，简而言之就是将Java类的字节码文件加载到机器内存中，并在内存中构建出Java类的原型——类模板对象。

所谓类模板对象，其实就是Java类在JVM内存中的一个快照，JVM将从字节码文件中解析出的常量池、类字段、类方法等信息存储到类模板中，这样JVM在运行期便能通过类模板而获取Java类中的任意信息，能够对Java类的成员变量进行遍历，也能进行Java方法的调用。

类模型的位置，加载的类在JVM中创建相应的类结构，类结构会存储在方法区(JDK1.8之前:永久代;JDK1.8及之后:元空间)。

一般来说加载分为以下几步：
(1) 通过一个类的全限定名获取此类的二进制字节流
(2) 将这个字节流所代表的静态存储结构转化为方法区的运行时数据结构
(3) 在内存中生成一个代表这个类的java.lang.Class对象，作为方法区这个类的各种数据的访问入口

1.3 验证

验证作为链接的第一步，用于确保类或接口的二进制表示结构上是正确的，从而确保字节流包含的信息对虚拟机来说是安全的。Java虚拟机规范中关于验证阶段的规则也是在不断增加的，但大体上会完成下面4个验证动作。

(1) 文件格式验证：主要验证字节流是否符合Class文件格式规范，并且能被当前版本的虚拟机处理。
(2) 元数据验证：主要对字节码描述的信息进行语义分析，以保证其提供的信息符合Java语言规范的要求。
(3) 字节码验证：主要是通过数据流和控制流分析，确定程序语义是合法的、符合逻辑的。在第二阶段对元数据信息中的数据类型做完校验后，字节码验证将对类的方法体进行校验分析，保证被校验类的方法在运行时不会做出危害虚拟机安全的事件。
(4) 符号引用验证：最后一个阶段的校验发生在虚拟机将符号引用转化为直接引用的时候，这个转化动作将在连接的第三阶段解析阶段发生。符号引用是对类自身以外（常量池中的各种符号引用）的信息进行匹配校验。

1.4 准备

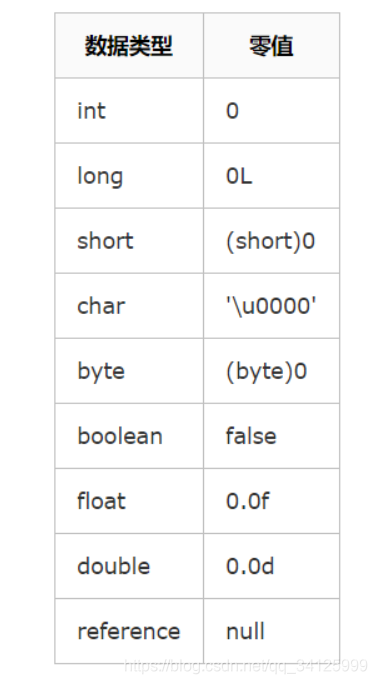
准备阶段的任务是为类或者接口的静态字段分配空间，并且默认初始化这些字段。这个阶段不会执行任何的虚拟机字节码指令，在初始化阶段才会显示的初始化这些字段，所以准备阶段不会做这些事情。

1.5 解析

解析阶段是把常量池内的符号引用替换成直接引用的过程。

符号引用（Symbolic References）：符号引用以一组符号来描述所引用的目标，符号可以是任何形式的字面量，只要可以唯一定位到目标即可。符号引用于内存布局无关，所以所引用的对象不一定需要已经加载到内存中。各种虚拟机实现的内存布局可以不同，但是接受的符号引用必须是一致的，因为符号引用的字面量形式已经明确定义在Class文件格式中。

直接引用（Direct References）：直接引用时直接指向目标的指针、相对偏移量或是一个能间接定位到目标的句柄。直接引用和虚拟机实现的内存布局相关，同一个符号引用在不同虚拟机上翻译出来的直接引用一般不会相同。如果有了直接引用，那么它一定已经存在于内存中了。

1.6 初始化

初始化是类加载的最后一步，在前面的阶段里，除了加载阶段可以通过用户自定义的类加载器加载，其余部分基本都是由虚拟机主导的。但是到了初始化阶段，才开始真正执行用户编写的java代码了。

在准备阶段，变量都被赋予了初始值，但是到了初始化阶段，所有变量还要按照用户编写的代码重新初始化。换一个角度，初始化阶段是执行类构造器()方法的过程。()方法是由编译器自动收集类中的所有类变量的赋值动作和静态语句块(static语句块)中的语句合并生成的，编译器收集的顺序是由语句在源文件中出现的顺序决定的，静态语句块中只能访问到定义在静态语句块之前的变量，定义在它之后的变量，在前面的静态语句块中可以赋值，但是不能访问。

2 类加载的时机

2.1 类在使用时才会加载

public class Test01 {public static void main(String[] args) {System.out.println(TestB.str);}static class TestA {public static String str = "A str";static {System.out.println("A static block");}}static class TestB extends TestA {static {System.out.println("B static block");}}
}

2.2 加载一个类的子类会加载父类

public class Test02 {public static void main(String[] args) {System.out.println(new TestB().str);}static class TestA {static {System.out.println("A static block");}}static class TestB extends TestA {public String str = "B str";static {System.out.println("B static block");}}}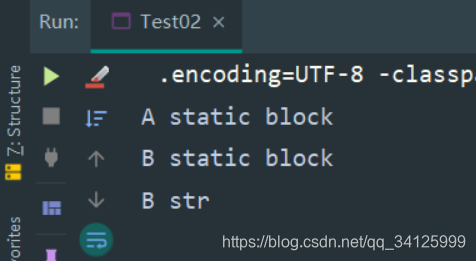

2.3 new 对象触发类的加载

public class Test03 {public static void main(String[] args) {TestA testA = new TestA();}static class TestA {static {System.out.println("TestA static block");}}}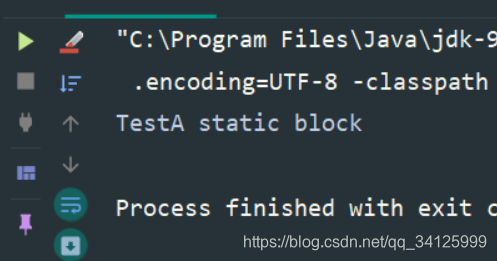

2.4 static final修饰的常量属性会存到常量池中，类不会加载

public class Test04 {public static void main(String[] args) {System.out.println(TestA.str);}static class TestA {public static final String str = "A str";static {System.out.println("TestA static block");}}}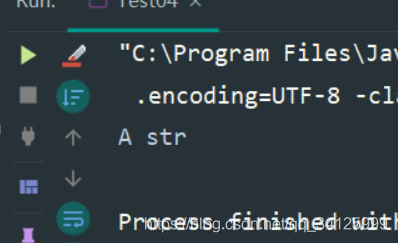

2.5 反射触发类加载

public class Test05 {static {System.out.println("Test05 static block");}public static void main(String[] args) throws ClassNotFoundException {Class<?> clazz = Class.forName("com.rosh.Test01");}}