讲透学烂二叉树(三)：二叉树的遍历图解算法步骤及JS代码

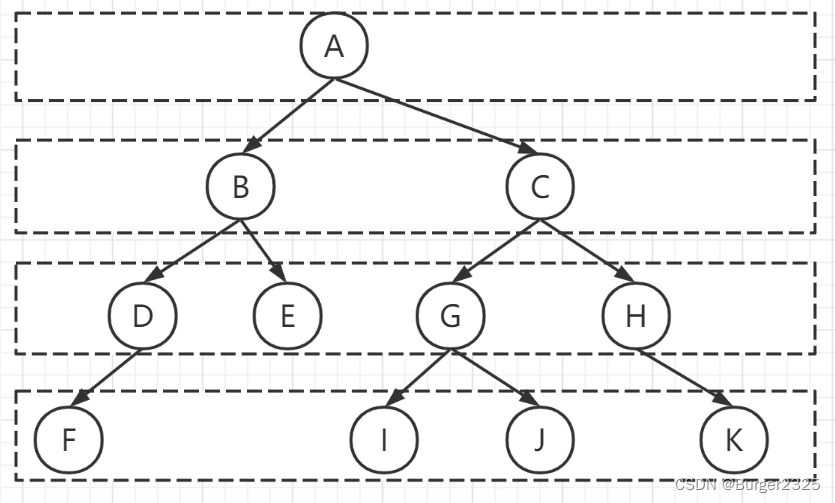
二叉树的遍历是指不重复地访问二叉树中所有结点，主要指非空二叉树，对于空二叉树则结束返回。

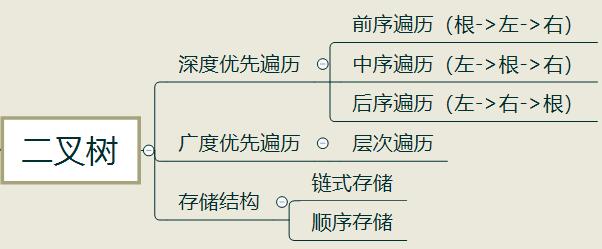
二叉树的遍历分为

深度优先遍历
- 先序遍历：根节点->左子树->右子树（根左右），有的叫：前序遍历
- 中序遍历：左子树->根节点->右子树（左根右）
- 后序遍历：左子树->右子树->根节点（左右根）
广度优先遍历
- 层次遍历：

二叉树-深度的优先遍历-图解

深度优先，前、中、后遍历顺序，就是组合[根左右]，移动根的位置，根左右、左根右、左右根，但是我即使代码会写了，还是搞不明白这个根左右与遍历的关系毛线头在哪里，特别是中序遍历的左根右，

博主YuXi_0520的图解，应该是我看过最易懂的。这里盗图贴一下

先序遍历（DLR）

先序遍历可以想象成，小人从树根开始绕着整棵树的外围转一圈，经过结点的顺序就是先序遍历的顺序

二叉树先序遍历流程图解

让我们来看下动画，和小人儿一起跑两遍就记住啦，记住是绕着外围跑哦

二叉树先序列遍历-gif动画演示

二叉树先序遍历小人动画演示

先序遍历结果：ABDHIEJCFKG

二叉树先序遍历-js代码实现

递归实现—二叉树先序遍历

根 - 左 - 右递归

判断根结点是否为空，为空则返回null；否则取结点的值，然后去左、右结点的值

/*** @description 前序遍历 =>1.访问根节点； 2.访问左子树； 3.访问右子树* @param node {Node} 遍历的树*/
preOrderTraverse (node = this.tree) {// 数组存储数遍历值let backs = []// 递归，function tempFunction (node) {if (node.data !== null) {// 先取根结点backs.push(node.data)// 如果存在左结点，取左节点的值node.leftChild && tempFunction(node.leftChild)// 如果存在右结点，取右结点值node.rightChild && tempFunction(node.rightChild)}}tempFunction(node)return backs
}

非递归-二叉树先序遍历

取结点的值，然后将左、右结点压如栈

preOrderTraverse2 (node = this.tree) {let backs = []if (!node) {return backs}let queue = [node]while (queue.length) {// 取出最后一个结点，对这个结点进行遍历let root = queue.pop()backs.push(root.data)// 因为queue.pop，所以先存入右结点root.rightChild && queue.push(root.rightChild)root.leftChild && queue.push(root.leftChild)}return backs
}

非递归-二叉树先序遍历

下面代码应该更容易理解

如果结点存在左结点，取值，然后存入栈中，直至没有左结点是叶子，再取右边

preOrderTraverse3 (node = this.tree) {let backs = []if (!node) {return backs}let currentNode = nodelet queue = [node]while (queue.length) {if(currentNode){backs.push(currentNode.data)queue.push(currentNode)currentNode=currentNode.leftChild}else {currentNode = queue.pop()currentNode = currentNode.rightChild}}return backs
}

中序遍历（LDR）

中序遍历可以想象成，按树画好的左右位置投影下来就可以了

二叉树-中序遍历-gif动图演示

下面看下投影的过程动画，其实就是按左右顺序写下来就行了

中序遍历结果：HDIBEJAFKCG

二叉树中序遍历-JavaScript代码实现

递归实现-二叉树中序遍历

/*** @description 中遍历 =>左右根* @param node {Node} 遍历的树*/
inOrderTraverse (node = this.tree) {// 数组存储数遍历值let backs = []// 递归，function tempFunction (node) {if (node.data !== null) {// 如果存在左结点，取左节点的值node.leftChild && tempFunction(node.leftChild)// 取根结点backs.push(node.data)// 如果存在右结点，取右结点值node.rightChild && tempFunction(node.rightChild)}}tempFunction(node)return backs
}

非递归实现-二叉树中序遍历

inOrderTraverse2(node){let backs = []if(!node){return backs}let stack = [node]let currentNode = nodewhile(stack.length){if(currentNode){stack.push(currentNode)currentNode = currentNode.leftChild}else {currentNode = stack.pop()backs.push(currentNode.data)currentNode = currentNode.rightChild}}
}

后序遍历（LRD）

后序遍历就像是剪葡萄，我们要把一串葡萄剪成一颗一颗的（从左到右，剪最底下的叶子结点）。

就是围着树的外围绕一圈，如果发现一剪刀就能剪下的葡萄（必须是一颗葡萄），就把它剪下来，组成的就是后序遍历了。

跟之前先序遍历绕圈的路线是一样的(先序遍历，是遇到结点，就push到数组），但是后续遍历是：递归：先取左叶结点（没有就跳过），再取右叶子结点

二叉树-后续遍历

二叉树-后续遍历-gif图

后序遍历结果：HIDJEBKFGCA

二叉树后续遍历-JavaScript代码实现

递归实现—二叉树后续遍历

/*** @description 后序遍历 =>左根右*  1.访问左子树。（先访问左子树中的左子树，再访问左子树中的右子树）*  2.访问右子树。（先访问右子树中的左子树，再访问右子树中的右子树）*  3.访问根* @param node {Node} 遍历的树*/
postOrderTraverse (node) {// 数组存储数遍历值let backs = []// 递归，function tempFunction (node) {if (node.data !== null) {// 如果存在左结点，取左节点的值node.leftChild && tempFunction(node.leftChild)// 如果存在右结点，取右结点值node.rightChild && tempFunction(node.rightChild)// 最后取根结点backs.push(node.data)}}tempFunction(node)return backs
}

非递归实现—二叉树后续遍历

postOrderTraverse2 (node){let backs = []if(!node){return backs}let stack  = [node]while(stack.length){let currentNode = stack.pop()backs.push(currentNode.data)currentNode.leftChild&&stack.push(currentNode.leftChild)currentNode.rightChild&&stack.push(currentNode.rightChild)}return  backs
}

非递归实现2—二叉树后续遍历

postOrderTraverse2 (node) {let backs = []if (!node) {return backs}let stack = []let currentNode = nodewhile (stack.length||currentNode) {if (currentNode) {stack.push(currentNode)backs .unshift(currentNode.data)currentNode = currentNode.rightChild} else {let temp = stack.pop()currentNode = temp.leftChild}}return backs
}

非递归实现3—二叉树后续遍历

postOrderTraverse3 (node) {let backs = []if (!node) {return backs}let stack = [node]while (stack.length) {let currentNode = stack.pop()backs.unshift(currentNode.data)currentNode.leftChild && stack.push(currentNode.leftChild)currentNode.rightChild && stack.push(currentNode.rightChild)}return backs
}

非递归实现4—二叉树后续遍历

postOrderTraverse4 (node) {let backs = []if (!node) {return backs}let stack = [node]let currentNode = nodelet visitedNode = nullwhile (stack.length) {if (currentNode) {stack.push(currentNode)currentNode = currentNode.leftChild} else {currentNode = stack[stack.length - 1]if (currentNode.rightChild && currentNode.rightChild !== visitedNode) {currentNode = currentNode.rightChild} else {backs.push(currentNode.data)visitedNode = currentNodestack.pop()currentNode = null}}}return backs
}

二叉树-广度优先遍历-图解

这个只有层序遍历

层序遍历

层序遍历太简单了，就是按照一层一层的顺序，从左到右写下来就行了。

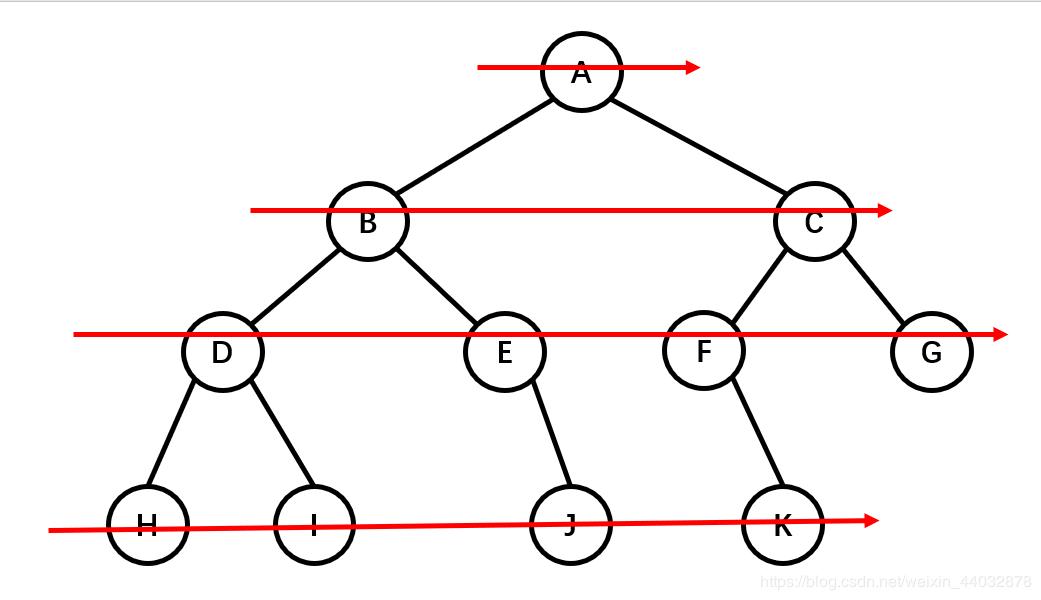
二叉树-广度优先-层序遍历

层序遍历结果：ABCDEFGHIJK

二叉序层序遍历-JavaScript代码实现

/*** @description 中遍历 =>左右根* @param node {Node} 遍历的树*/
inOrderTraverse (node = this.tree) {// 数组存储数遍历值let backs = []// 递归，function tempFunction (node) {if (node.data !== null) {// 如果存在左结点，取左节点的值node.leftChild && tempFunction(node.leftChild)// 取根结点backs.push(node.data)// 如果存在右结点，取右结点值node.rightChild && tempFunction(node.rightChild)}}tempFunction(node)return backs
}

不知道通过这种方式，有没有觉得闭着眼睛都能写出前序、中序、后序、层序了呀，不过这只是为了大家好理解，我想出的一种形象思维，为了用代码实现，我们还需要具体了解一下前序、中序、后序遍历。

真正理解三种遍历

还记得我们先序和后序遍历时候跑的顺序么？按照这个顺序再跑一次，就是围着树的外围跑一整圈。

让我们来理解一下绕着外围跑一整圈的真正含义是：遍历所有结点时，都先往左孩子走，再往右孩子走。

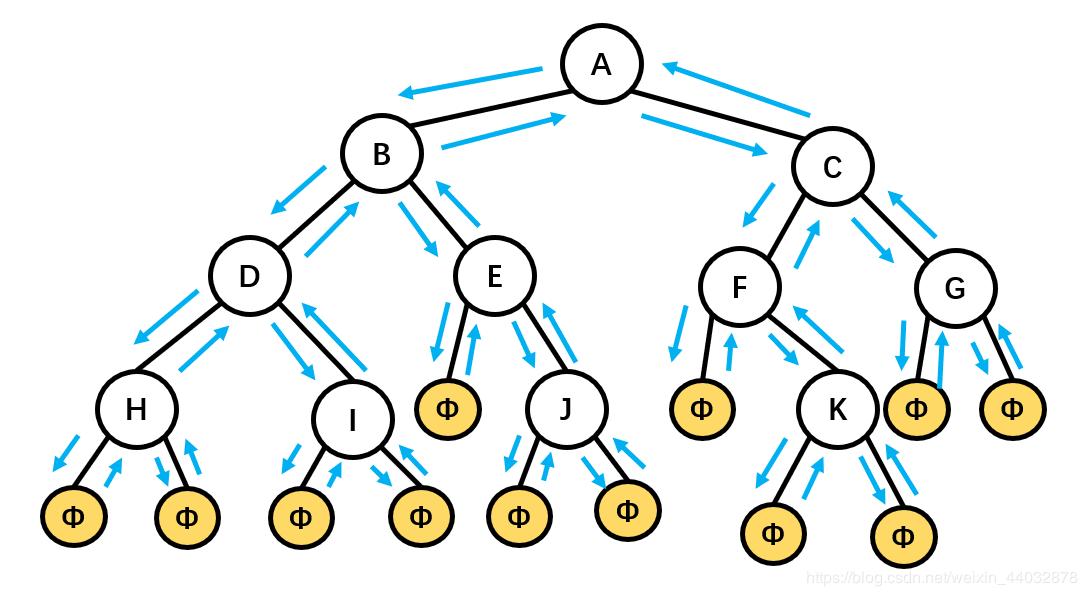
二叉树-先序与后续遍历流程图

观察一下，你有什么发现？

有没有发现，除了根结点和空结点，其他所有结点都有三个箭头指向它。

一个是从它的父节点指向它，
一个是从它的左孩子指向它
一个是从它的右孩子指向它。

一个结点有三个箭头指向它，说明每个结点都被经过了三遍。

一遍是从它的父节点来的时候，
一遍是从它的左孩子返回时，
一遍是从它的右孩子返回时。

其实我们在用递归算法实现二叉树的遍历的时候，不管是先序中序还是后序，程序都是按照上面那个顺序跑遍所有结点的。

先序中序和后序唯一的不同就是，在经过结点的三次中，哪次访问（输出或者打印或者做其他操作）了这个结点。有点像大禹治水三过家门，他会选择一次进去。

先序遍历顾名思义，就是在第一次经过这个结点的时候访问了它。就是从父节点来的这个箭头的时候，访问了它。
中序遍历也和名字一样，就是在第二次经过这个结点的时候访问了它。就是从左孩子返回的这个箭头的时候，访问了它。
后序遍历，就是在第三次经过这个结点的时候访问了它。就是从右孩子返回的这个箭头的时候，访问了它。

怎么样，这样有没有很好的理解？

其实不管是前序中序还是后序，在程序里跑的时候都是按照同样的顺序跑的，每个结点经过三遍，第几遍访问这个结点了，就叫什么序遍历。

当我们脑子里有这个概念的时候，再去看实现代码就很好理解了，下一篇博文我会贴出和讲解具体的实现代码。

如果递归分治来理解前、中、后遍历与根左右、左根右、左右根的关系，就是按照那个跑路图，对每个最底层的子结点[前、中、后]对应[根左右、左根右、左右根]顺序来处理。

二叉树前序、中序、后序遍历相互求法

已知二叉树的广度优先遍历-层序遍历数组，是可以完全还原二叉树结构，但是

已知二叉树前序、中序、后序中的一种排序数组，是无法求出二叉树结构的。但是知道前序、中序、后序中的中序和前序或后序数组两种也可以还原二叉树，为何可以推出二叉树的数据结构。

前序根结点在最前，后续根结点在最后，如果已知前序或者后续，则中序中根结点两边的元素分布为根结点的左边结点和右边结点元素。具体操作如下：

已知前序、中序遍历，求后序遍历

前序遍历=ABGDECFH
中序遍历=GBEDAFCH

构建二叉树步骤：

根据前序遍历的特点，我们知道根结点root为A；
观察中序遍历GBEDAFCH。其中root节点A的左侧GBED必然是root的左子树，右侧FCH必然是root的右子树。同时，这个也分别是左子树和右子树的中序遍历的序列；
在前序遍历遍历完根节点后，接着执行前序遍历左子树，注意，是前序遍历，什么意思？就是把左子树当成一棵独立的树，执行前序遍历，同样先访问左子树的根，第2步我们已经知道左子树是BGDE（前序遍历序列）了，由此可以得到，左子树的根是B，那么在这一步得到左子树的根是B；
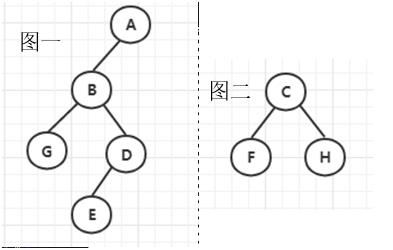
从第2步得到的中序遍历的节点序列中，找到B，发现B左边只有一个G，说明B的左子树只有一个叶子节点，B的右边呢？我们可以得到B的右子树有ED，再看前序遍历的序列，发现D在前，也就是说，D是先前序遍历访问的，则得到E是D的左子树，只有一个叶子节点。到这里，我们可以得到这棵树的根结点和左子树的结构了，如下图一
接着看右子树，在第2步的时候已经知道右子树是FCH这三个节点，那么先看前序遍历的序列，先出现的是C，那么C就是右子树的根结点，看右子树的中序遍历为FCH，所以F和H就分别是它的左子树和右子树，因此，右子树的结构就出来了，如下图二

二叉树线序与中序，还原二叉树