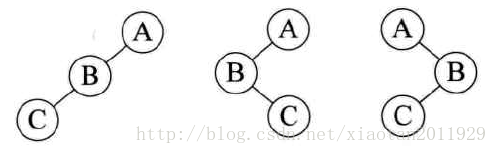
遍历一棵二叉树有很多种方法。假如用D、L、R分别代表二叉树的根结点、左子树、右子树,那么要遍历这棵二叉树,方法就有6种:DLR、DRL、LDR、LRD、RDL、RLD。一般在遍历时遵循先左后右的原则,因此常用的遍历方法有三种:DLR,称为先(根)序遍历;LDR,称为中(根)序遍历;LRD,称为后(根)序遍历。
先序遍历
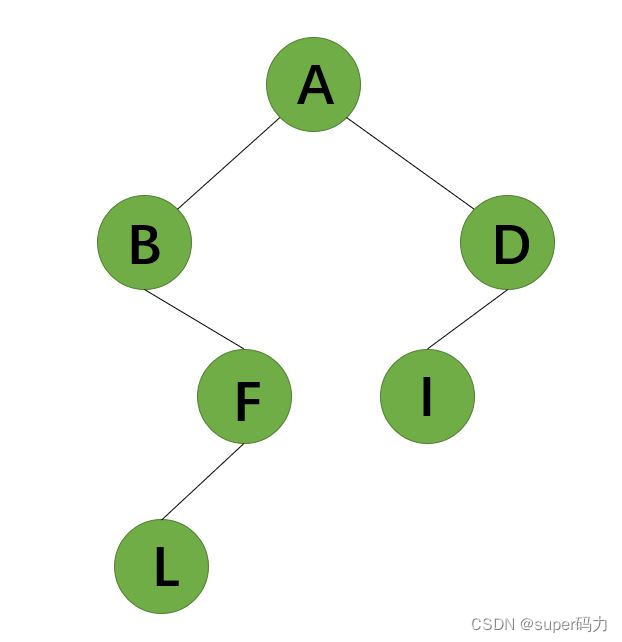
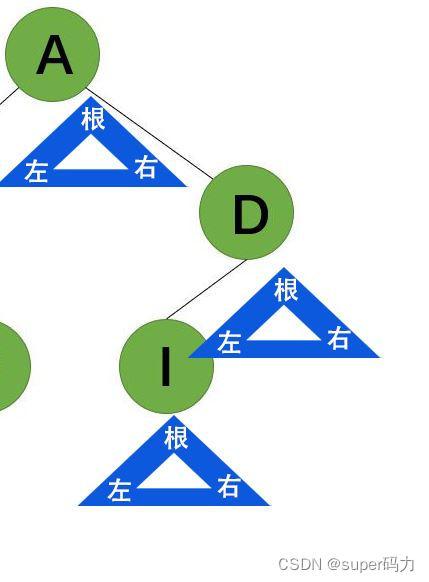
先序遍历是指在遍历二叉树时先访问根结点,然后访问左子树,最后访问右子树。例如下图的二叉树,使用先序遍历访问的结果是ABFLDI。
tips:可以想象有一个标记着“根左右”的三角形每到一个结点时让三角形的根与之对应来看。
先序遍历过程是这样的(根左右):
第一步:访问根结点,输出A。
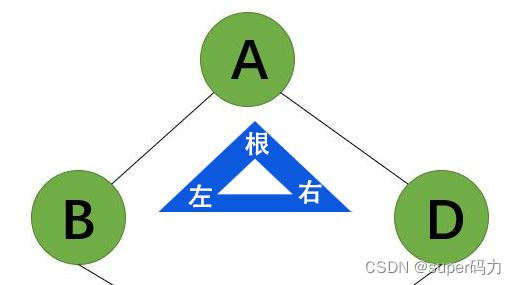
第二步:访问左子树,左子树是以B为根结点的二叉树。所以输出B。
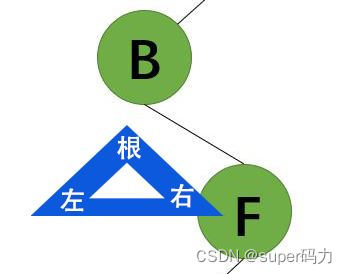
第三步:访问B的左子树,发现没有左子树,则访问右子树,右子树是以F为根结点的二叉树。所以输出F。
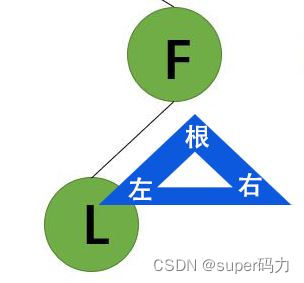
第四步:访问F的左子树,左子树是以L为根结点的左子树。所以输出L。
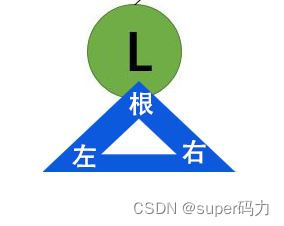
第五步:访问L的左子树,发现L没有左子树,则访问右子树,L没有右子树,表示以L为根结点的二叉树访问完毕,同时也代表着F的左子树访问完毕。
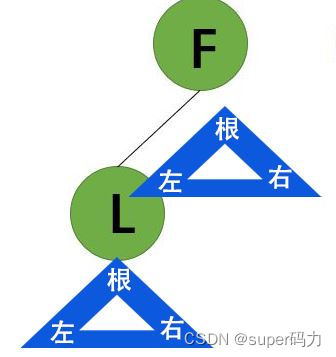
第六步:访问F的右子树,发现没有右子树,表示以F为根结点的二叉树访问完毕,同时也代表着B的右子树访问完毕,也代表着A的左子树访问完毕。
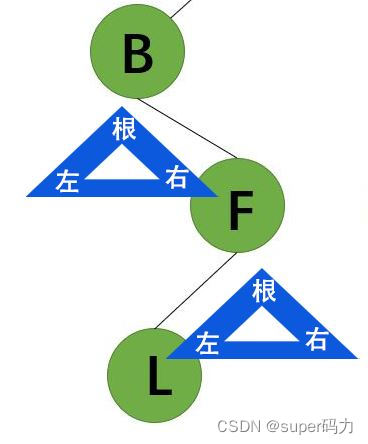
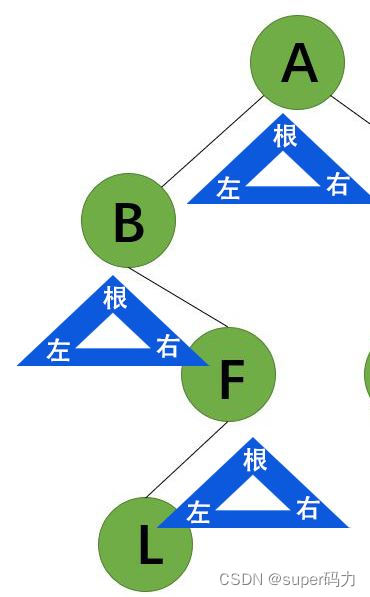
第七步:访问A的右子树,右子树是以D为根结点的二叉树。所以输出D。
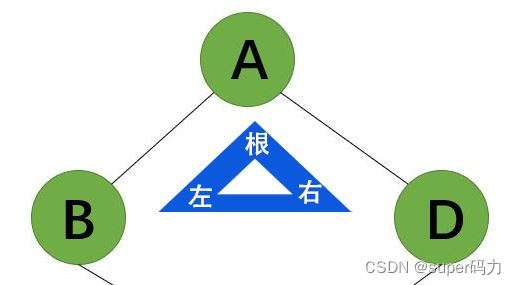
第八步:访问D的左子树,左子树是以I为根结点的二叉树。所以输出I。
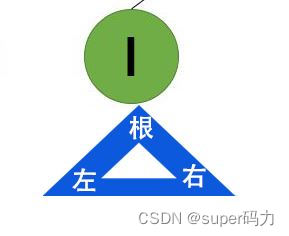
第九步:访问I的的左子树,发现没有左子树,则访问I右子树,发现也没有右子树,则表示已I为根结点的二叉树访问结束,同时也代表D的左子树访问结束。
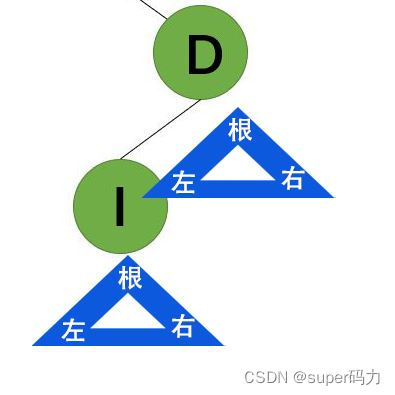
第十步:访问D的右子树,发现没有右子树,则表示以D为根结点的二叉树访问结束,同时也代表A的右子树访问结束,整棵树遍历完成。
中序遍历
中序遍历是指在遍历二叉树时先访问左子树,然后访问根结点,最后访问右子树。例如下面的二叉树,使用中序遍历访问的结果是BLFAID。
tips:遍历的第一个值查找,一开始就目标明确的找最底层的左子树并输出,再开始按照左根右的方式去依依输出,一层一层往上。
根据先序遍历同理可得,中序遍历过程是(左根右):
- 先访问根结点A的左子树,左子树是B为根结点的二叉树,再访问B的左子树,B没有左子树,则访问根结点B,输出B;
- 接着访问B的右子树,右子树是以F为根结点的二叉树;
- 继续访问F的左子树,F的左子树是以L为根结点的二叉树;
- 再继续访问L的左子树,左子树不存在,则访问根结点L,输出L;
- 然后访问L的右子树,右子树不存在,则表示以L为根结点的二叉树访问结束,同时也代表着F的左子树访问结束,访问根结点F,输出F;
- 访问F的右子树,不存在,则F为根结点的二叉树访问完毕,同时也表示以B为根结点的右子树访问完毕;
- 访问根结点A,并输出A;
- 访问A的右子树,A的右子树是以D为根结点的二叉树,继续访问D的左子树,左子树是以I为根结点的二叉树,再继续访问I的左子树,不存在,则访问根结点I,并输出I;
- 接着访问I的右子树,没有,则表示以I为根结点的二叉树访问完毕,同时也表示D的左子树访问完毕,然后访问根结点D,并输出D;
- 访问D的右子树,不存在,表示以D为根结点的二叉树访问结束,同时也代表着A的右子树访问完毕,整个遍历结束。
后序遍历
后序遍历是指在遍历二叉树时先访问树的左子树,然后访问右子树,最后访问根结点。有了先序遍历和中序遍历的经验,后序遍历对大家来说已经不在话下了,可以尝试一下去遍历下图的二叉树。答案在最后面。
树是递归定义的,在遍历二叉树时也用到了递归,首先将整棵二叉树当作有三个单元的结构:根节点、左子树、右子树。遍历完根结点,开始遍历左子树,把左子树当成一棵独立的二叉树来遍历;同样,当遍历右子树时,也将右子树当成一棵独立的二叉树来遍历,这就是递归思想。

答案:后序遍历访问的结果是LFBIDA。