二叉树的遍历方式是最基本，也是最重要的一类题目，我们将从「前序」、「中序」、「后序」、「层序」四种遍历方式出发，总结他们的递归和迭代解法。

一、二叉树定义
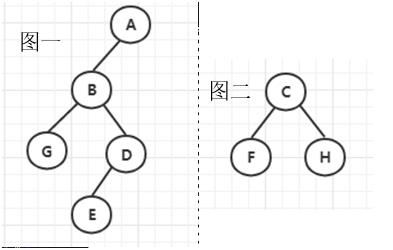
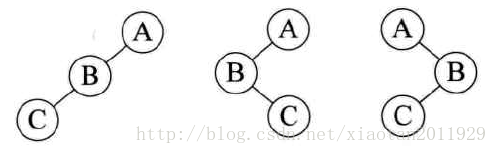
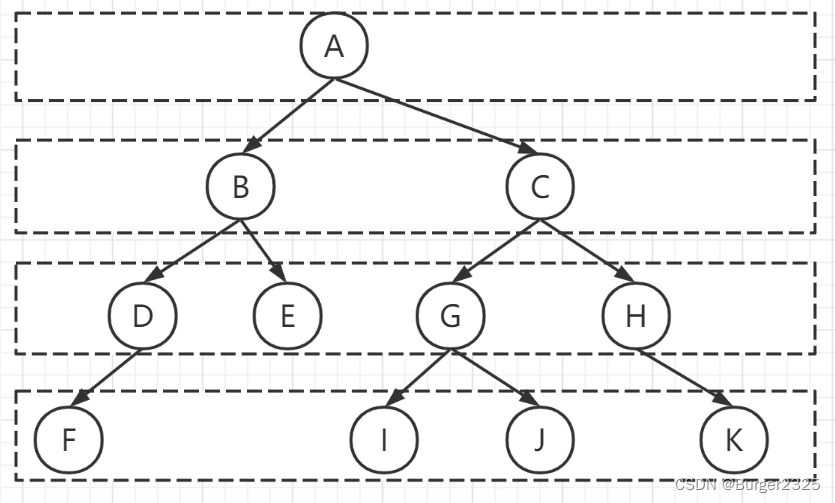
      二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个结点最多只能有两棵子树，且有左右之分。简单来说，就是一个包含节点，以及它的左右孩子的一种数据结构

假设二叉树的节点定义如下

public class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode() {}public TreeNode(int val) {this.val = val;}public TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}

二、层序遍历

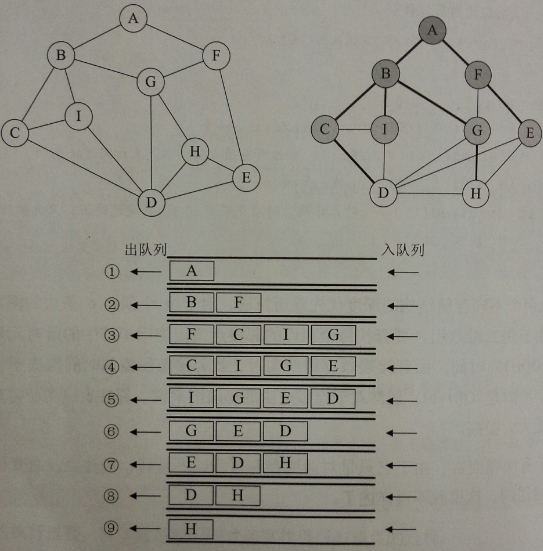
层序遍历比较简单，按照从上到下，从左到右的顺序逐次遍历。此处借用队列的先入先出特性来实现，具体代码如下

public static void levelTraverse(TreeNode root) {if (root == null) {return;}Queue<TreeNode> queue = new LinkedList<>();//初始化时把root放入队列queue.offer(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();//打印节点的值System.out.print(node.val + " ");//队列是先入先出，所以此处先遍历左节点if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}}

三、前序遍历（根节点，左子树，右子树）

1、递归实现：二叉树遍历的递归形式比较容易实现，直接按照根节点，左子树，右子树的顺序 逐次遍历即可

private static void preOrderTraversal0(TreeNode root) {if (root == null) {return;}//打印根节点System.out.print(root.val + " ");//打印左节点preOrderTraversal0(root.left);//打印右节点preOrderTraversal0(root.right);}

2、迭代实现

2.1 迭代解法一

过程如下：

• 初始化栈，并将根节点入栈；

• 当栈不为空时：
  弹出栈顶元素 node，并将值添加到结果中；
  如果 node 的右子树非空，将右子树入栈；
  如果 node 的左子树非空，将左子树入栈；
  由于栈是“先进后出”的顺序，所以入栈时先将右子树入栈，这样使得前序遍历结果为 “根->左->右”的顺序。

经过上面图的讲解，代码就比较简单，代码如下：

private static void preOrderTraversal1(TreeNode root) {if (null == root) {return;}//定义一个栈方便后续遍历Stack<TreeNode> stack = new Stack<>();//初始化stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();//每一次出栈都打印节点的值System.out.print(node.val + " ");//栈是先进后出的，所以先处理右子树入栈，再左子树入栈if (node.right != null) {stack.push(node.right);}if (node.left != null) {stack.push(node.left);}}}

2.2 迭代解法二

（1）思路稍有不同，先定义一个节点cur指向root节点，先将cur节点和所有的左孩子入栈同时打印出cur节点的值，直至 cur 为空，用一个 while 循环实现。

（2）随后出栈一个节点，定义为node，执行 cur = node.right，随后继续执行 操作（1）

经过上面分析，代码中的（1）和（2）分别对应上述的描述，代码如下：

private static void preOrderTraversal2(TreeNode root) {if (root == null) {return;}Stack<TreeNode> stack = new Stack<>();//定义一个cur指向rootTreeNode cur = root;while (!stack.isEmpty() || cur != null) {//（1）只要cur！=null，则打印值，同时cur入栈，同时设置cur = cur.leftwhile (cur != null) {System.out.print(cur.val + " ");stack.push(cur);cur = cur.left;}//（2）如果cur == null,则出栈一个节点，同时设置cur = node.right,同时继续执行（1）TreeNode node = stack.pop();cur = node.right;}}

四、中序遍历（左子树，根节点，右子树）

1、递归实现：二叉树遍历的递归形式比较容易实现，直接按照（左子树，根节点，右子树）的顺序 逐次遍历即可

//中序遍历private static void inOrderTraversal0(TreeNode root) {if (root == null) {return;}//打印左节点inOrderTraversal0(root.left);//打印根节点System.out.print(root.val + " ");//打印右节点inOrderTraversal0(root.right);}

2、迭代解法：（左子树，根节点，右子树）

（1）与前序遍历的逻辑差不多，前序遍历是入栈的时候打印值，但是中序遍历是先处理左节点，再处理根节点，最后遍历右节点，所以遍历时不打印值，出栈时打印值，先定义一个节点cur指向root节点，先将cur节点和所有的左孩子入栈 直至 cur 为空，用一个 while 循环实现。

（2）随后出栈一个节点，定义为node，打印节点的值，执行 cur = node.right，随后继续执行 操作（1）

经过上面处理后 root 节点的左子树处理完毕，接下来继续处理右子树，也是重复的过程，经过上面分析，代码如下：

private static void inOrderTraversal1(TreeNode root) {if (root == null) {return;}TreeNode cur = root;Stack<TreeNode> stack = new Stack<>();while (!stack.isEmpty() || cur != null) {//（1）如果cur不等于空，一直入栈，同时执行cur = cur.left,目的是找到最左节点while (cur != null) {stack.push(cur);cur = cur.left;}//(2)如果cur为空，则出栈一个元素，同时打印值，接下来处理右子树，右子树也是调用（1）同步处理TreeNode node = stack.pop();System.out.print(node.val + " ");cur = node.right;}}

五、后续遍历（左子树，右子树，根节点）

1、递归实现：二叉树遍历的递归形式比较容易实现，直接按照（左子树，右子树，根节点）的顺序 逐次遍历即可

private static void postOrderTraversal0(TreeNode root) {if (root == null) {return;}//打印左节点postOrderTraversal0(root.left);//打印右节点postOrderTraversal0(root.right);//打印根节点System.out.print(root.val + " ");}

2、迭代实现：（二叉树的后续遍历，先左子树，右子树，最后根结点），可以定义两个辅助栈，一个栈用于辅助遍历，一个栈用于存放结果，从root开始遍历时先遍历到跟结点，但是根节点又需要最后输出，所以可以借助栈的（先进后出的）特性实现先进入的节点最后输出

经过上面的图解代码如下：

public static void postOrderTraversal(TreeNode root) {if (root == null) {return;}Stack<TreeNode> stack1 = new Stack<TreeNode>();//起始时root入栈stack1.push(root);//定义一个result栈Stack<TreeNode> result = new Stack<TreeNode>();while (!stack1.isEmpty()) {TreeNode node = stack1.pop();result.push(node);//先左节点入栈if (node.left != null) {stack1.push(node.left);}//再右节点入栈if (node.right != null) {stack1.push(node.right);}}//最后result栈中依次出栈即为结果while (!result.isEmpty()) {System.out.print(result.pop().val + " ");}}

上面仅记录个人的理解。有错误麻烦指正，感谢。