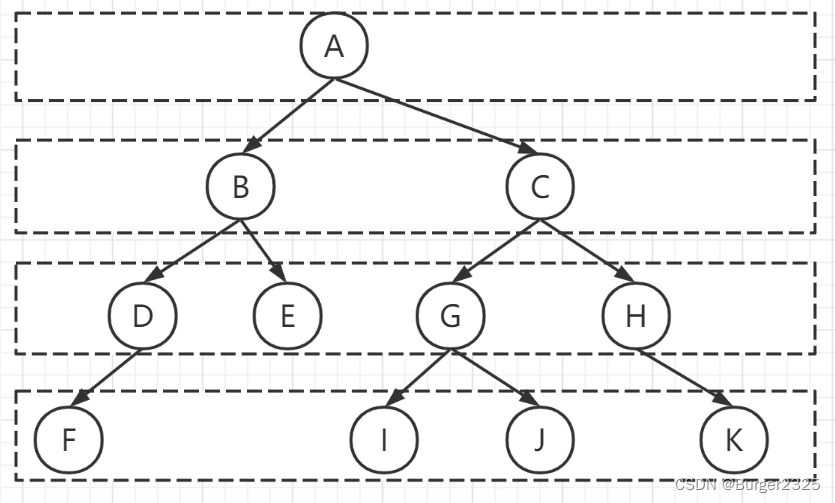
二叉树的遍历方法

一.二叉树分类：

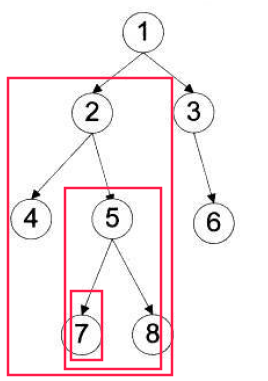
完全二叉树
满二叉树
扩充二叉树
平衡二叉树

二.二叉树的四种遍历方式：

前序遍历（先根，再左，最后右）
中序遍历（先左，再根，最后右）
后序遍历（先左，再右，最后根）
层次遍历（说不清）

1.递归遍历

（1）前序遍历

遍历方法：先根节点，再左节点，最后右节点。

在这里图片描述
实现代码：

/*声明结点TreeNode类*/
public static void preOrderTraveral(TreeNode node){if(node == null){return;}System.out.print(node.data+" ");preOrderTraveral(node.leftChild);preOrderTraveral(node.rightChild);
}/*再来创建一颗二叉树：*/
public static TreeNode createBinaryTree(LinkedList<Integer> list){TreeNode node = null;if(list == null || list.isEmpty()){return null;}Integer data = list.removeFirst();if(data!=null){node = new TreeNode(data);node.leftChild = createBinaryTree(list);node.rightChild = createBinaryTree(list);}return node;
}

（2）中序遍历

先左节点，再根节点，最后右节点
在这里插入图片描述
实现代码：

public static void inOrderTraveral(TreeNode node){if(node == null){return;}inOrderTraveral(node.leftChild);System.out.print(node.data+" ");inOrderTraveral(node.rightChild);
}

（3）后序遍历

先左节点，再右节点，最后根节点
在这里插入图片描述
实现代码：

public static void postOrderTraveral(TreeNode node){if(node == null){return;}postOrderTraveral(node.leftChild);postOrderTraveral(node.rightChild);System.out.print(node.data+" ");
}

答案：

前序遍历结果为：ABDFECGHI；
中序遍历结果为：DBEFAGHCI；
后序遍历结果为：DEFBHGICA

2.非递归遍历：

（1）前序遍历

public static void preOrderTraveralWithStack(TreeNode node){Stack<TreeNode> stack = new Stack<TreeNode>();TreeNode treeNode = node;while(treeNode!=null || !stack.isEmpty()){//迭代访问节点的左孩子，并入栈while(treeNode != null){System.out.print(treeNode.data+" ");stack.push(treeNode);treeNode = treeNode.leftChild;}//如果节点没有左孩子，则弹出栈顶节点，访问节点右孩子if(!stack.isEmpty()){treeNode = stack.pop();treeNode = treeNode.rightChild;}}
}

（2）中序遍历

public static void inOrderTraveralWithStack(TreeNode node){Stack<TreeNode> stack = new Stack<TreeNode>();TreeNode treeNode = node;while(treeNode!=null || !stack.isEmpty()){while(treeNode != null){stack.push(treeNode);treeNode = treeNode.leftChild;}if(!stack.isEmpty()){treeNode = stack.pop();System.out.print(treeNode.data+" ");treeNode = treeNode.rightChild;}}
}

（3）后序遍历

public static void postOrderTraveralWithStack(TreeNode node){Stack<TreeNode> stack = new Stack<TreeNode>();TreeNode treeNode = node;TreeNode lastVisit = null;   //标记每次遍历最后一次访问的节点//节点不为空，结点入栈，并且指向下一个左孩子while(treeNode!=null || !stack.isEmpty()){while(treeNode!=null){stack.push(treeNode);treeNode = treeNode.leftChild;}//栈不为空if(!stack.isEmpty()){//出栈treeNode = stack.pop();/*** 这块就是判断treeNode是否有右孩子，* 如果没有输出treeNode.data，让lastVisit指向treeNode，并让treeNode为空* 如果有右孩子，将当前节点继续入栈，treeNode指向它的右孩子,继续重复循环*/if(treeNode.rightChild == null || treeNode.rightChild == lastVisit) {System.out.print(treeNode.data + " ");lastVisit = treeNode;treeNode  = null;}else{stack.push(treeNode);treeNode = treeNode.rightChild;}}}
}

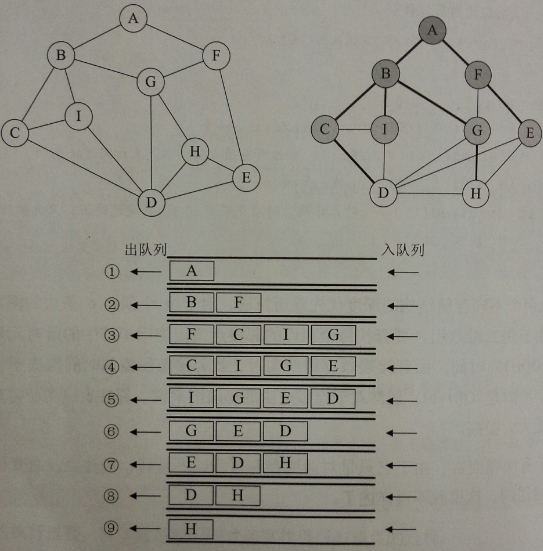
3.层次遍历

public static void levelOrder(TreeNode root){LinkedList<TreeNode> queue = new LinkedList<>();queue.add(root);while(!queue.isEmpty()){root = queue.pop();System.out.print(root.data+" ");if(root.leftChild!=null) queue.add(root.leftChild);if(root.rightChild!=null) queue.add(root.rightChild);}
}