二叉树的各种遍历算法以及实例

article/2025/9/22 6:47:50

一、二叉树

在计算机科学中，树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构。二叉树是每个节点最多有两个子树的有序树。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。值得注意的是，二叉树不是树的特殊情形。在图论中，二叉树是一个连通的无环图，并且每一个顶点的度不大于3。有根二叉树还要满足根结点的度不大于2。有了根结点后，每个顶点定义了唯一的根结点，和最多2个子结点。然而，没有足够的信息来区分左结点和右结点。二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2的 i -1次方个结点；深度为k的二叉树至多有2^(k) -1个结点；对任何一棵二叉树T，如果其终端结点数(即叶子结点数)为n0，度为2的结点数为n2，则n0 = n2 + 1。 

二、二叉树的遍历

前序遍历（DLR）

前序遍历也叫做先根遍历，可记做根左右。
前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树。
若二叉树为空则结束返回，否则：
  （ 1 ）访问根结点
  （ 2 ）前序遍历左子树
  （ 3 ）前序遍历右子树
注意的是：遍历左右子树时仍然采用前序遍历方法。

中序遍历（LDR）

中序遍历也叫做中根遍历，可记做左根右。
中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。在遍历左、右子树时，仍然先遍历左子树，再访问根结点，最后遍历右子树。即：
若二叉树为空则结束返回，否则：

（1）中序遍历左子树
（2）访问根结点
（3）中序遍历右子树。
注意的是：遍历左右子树时仍然采用中序遍历方法。

后序遍历（LRD）

后序遍历也叫做后根遍历，可记做左右根。
后序遍历首先遍历左子树，然后遍历右子树，最后访问根结点。在遍历左、右子树时，仍然先遍历左子树，再遍历右子树，最后访问根结点。即：
若二叉树为空则结束返回，否则：
（ 1 ）后序遍历左子树。
（ 2 ）后序遍历右子树。
（ 3 ）访问根结点。
注意的是：遍历左右子树时仍然采用后序遍历方法。 

层次遍历

按照从上至下，从左至右的顺序遍历二叉树。

 

图1-1 二叉树遍历用例图
如上图所示二叉树

前序遍历，也叫先根遍历，遍历的顺序是，根，左子树，右子树
遍历结果：A,B,E,F,C,G
中序遍历，也叫中根遍历，顺序是 左子树，根，右子树
遍历结果：E,B,F,A,G,C
后序遍历，也叫后根遍历，遍历顺序，左子树，右子树，根
遍历结果：E,F,B,G,C,A

层次遍历结果：A,B,C,E,F,G 

二叉树的链式存储结构是一类重要的数据结构，其形式定义如下： 

//二叉树结点
typedef struct BiTNode{
//数据
char data;
//左右孩子指针
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree; 

二叉树的创建：

通过读入一个字符串，建立二叉树的算法如下： 

//按先序序列创建二叉树
int CreateBiTree(BiTree &T){
char data;
//按先序次序输入二叉树中结点的值（一个字符），‘#’表示空树
scanf("%c",&data);
if(data == '#'){
T = NULL;
}
else{
T = (BiTree)malloc(sizeof(BiTNode));
//生成根结点
T->data = data;
//构造左子树
CreateBiTree(T->lchild);
//构造右子树
CreateBiTree(T->rchild);
}
return 0;
}

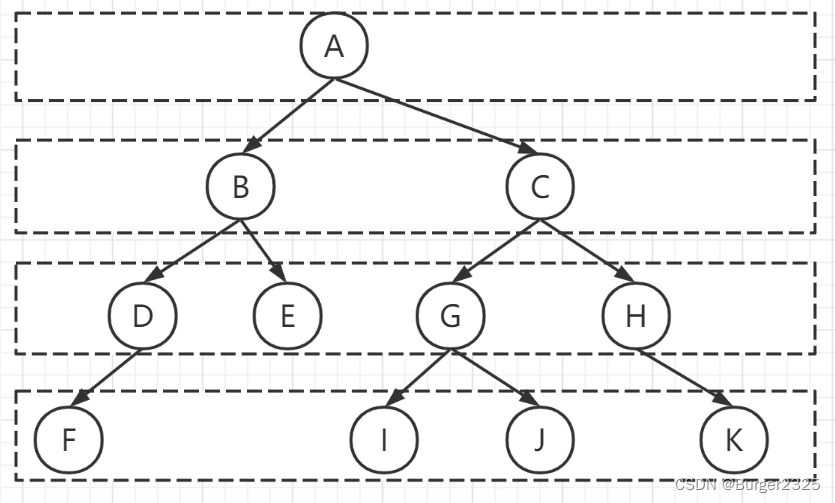
注意：创建二叉树的算法中，字符串的输入必须是按先序次序输入，先序遍历二叉树时空树以#代替，以图1-1为例，应该输入的字符串顺序为：ABE##F##CG###（最后一个#是结束符），“#”表示空树，如下图所示：

 

二叉树的遍历：

遍历是对树的一种最基本的运算，所谓遍历二叉树，就是按一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次。由于二叉树是非线性结构，因此，树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。

递归算法：

输出二叉树的字符序列，以 '#' 结束。先访问根节点，然后访问左节点，再访问右节点。

//输出
void Visit(BiTree T){
if(T->data != '#'){
printf("%c ",T->data);
}
} 
//先序遍历
void PreOrder(BiTree T){
if(T != NULL){
//访问根节点
Visit(T);
//访问左子结点
PreOrder(T->lchild);
//访问右子结点
PreOrder(T->rchild);
}
}

中序遍历，先访问左节点，然后访问根节点，再访问右节点。

void InOrder(BiTree T){
if(T != NULL){
//访问左子结点
InOrder(T->lchild);
//访问根节点
Visit(T);
//访问右子结点
InOrder(T->rchild);
}
}

后序遍历，先访问左节点，然后访问右节点，再访问根节点。

 

void PostOrder(BiTree T){
if(T != NULL){
//访问左子结点
PostOrder(T->lchild);
//访问右子结点
PostOrder(T->rchild);
//访问根节点
Visit(T);
}
}

非递归算法：

<1>先序遍历：

【思路】：访问T->data后，将T入栈，遍历左子树；遍历完左子树返回时，栈顶元素应为T，出栈，再先序遍历T的右子树。其实每次都是走树的左分支(left)，直到左子树为空，然后开始从递归的最深处返回，然后开始恢复递归现场，访问右子树。 

/* 先序遍历(非递归)思路：访问T->data后，将T入栈，遍历左子树；遍历完左子树返回时，栈顶元素应为T，出栈，再先序遍历T的右子树。
*/
void PreOrder2(BiTree T){
stack<BiTree> stack;
//p是遍历指针
BiTree p = T;
//栈不空或者p不空时循环
while(p || !stack.empty()){
if(p != NULL){
//存入栈中
stack.push(p);
//访问根节点
printf("%c ",p->data);
//遍历左子树
p = p->lchild;
}
else{
//退栈
p = stack.top();
stack.pop();
//访问右子树
p = p->rchild;
}
}//while
} 

<2>中序遍历

【思路】：T是要遍历树的根指针，中序遍历要求在遍历完左子树后，访问根，再遍历右子树。
         先将T入栈，遍历左子树；遍历完左子树返回时，栈顶元素应为T，出栈，访问T->data，再中序遍历T的右子树。 

void InOrder2(BiTree T){
stack<BiTree> stack;
//p是遍历指针
BiTree p = T;
//栈不空或者p不空时循环
while(p || !stack.empty()){
if(p != NULL){
//存入栈中
stack.push(p);
//遍历左子树
p = p->lchild;
}
else{
//退栈，访问根节点
p = stack.top();
printf("%c ",p->data);
stack.pop();
//访问右子树
p = p->rchild;
}
}//while
} 

<3>后序遍历

【思路】：T是要遍历树的根指针，后序遍历要求在遍历完左右子树后，再访问根。需要判断根结点的左右子树是否均遍历过。 

//后序遍历(非递归)
typedef struct BiTNodePost{
BiTree biTree;
char tag;
}BiTNodePost,*BiTreePost; 
void PostOrder2(BiTree T){
stack<BiTreePost> stack;
//p是遍历指针
BiTree p = T;
BiTreePost BT;
//栈不空或者p不空时循环
while(p != NULL || !stack.empty()){
//遍历左子树
while(p != NULL){
BT = (BiTreePost)malloc(sizeof(BiTNodePost));
BT->biTree = p;
//访问过左子树
BT->tag = 'L';
stack.push(BT);
p = p->lchild;
}
//左右子树访问完毕访问根节点
while(!stack.empty() && (stack.top())->tag == 'R'){
BT = stack.top();
//退栈
stack.pop();
BT->biTree;
printf("%c ",BT->biTree->data);
}
//遍历右子树
if(!stack.empty()){
BT = stack.top();
//访问过右子树
BT->tag = 'R';
p = BT->biTree;
p = p->rchild;
}
}//while
}

<4>层次遍历

【思路】：按从顶向下，从左至右的顺序来逐层访问每个节点，层次遍历的过程中需要用队列。

//层次遍历
void LevelOrder(BiTree T){
BiTree p = T;
//队列
queue<BiTree> queue;
//根节点入队
queue.push(p);
//队列不空循环
while(!queue.empty()){
//对头元素出队
p = queue.front();
//访问p指向的结点
printf("%c ",p->data);
//退出队列
queue.pop();
//左子树不空，将左子树入队
if(p->lchild != NULL){
queue.push(p->lchild);
}
//右子树不空，将右子树入队
if(p->rchild != NULL){
queue.push(p->rchild);
}
}
}

以图1-1为测试用例

输入：ABE##F##CG### 

输出结果：

 

 完整代码：

// BinaryTree.cpp : 定义控制台应用程序的入口点
#include "stdafx.h"
#include<iostream>
#include<stack>
#include<queue>
using namespace std;//二叉树结点
typedef struct BiTNode{//数据char data;//左右孩子指针struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;//按先序序列创建二叉树
int CreateBiTree(BiTree &T){char data;//按先序次序输入二叉树中结点的值（一个字符），‘#’表示空树scanf("%c",&data);if(data == '#'){T = NULL;}else{T = (BiTree)malloc(sizeof(BiTNode));//生成根结点T->data = data;//构造左子树CreateBiTree(T->lchild);//构造右子树CreateBiTree(T->rchild);}return 0;
}
//输出
void Visit(BiTree T){if(T->data != '#'){printf("%c ",T->data);}
}
//先序遍历
void PreOrder(BiTree T){if(T != NULL){//访问根节点Visit(T);//访问左子结点PreOrder(T->lchild);//访问右子结点PreOrder(T->rchild);}
}
//中序遍历  
void InOrder(BiTree T){  if(T != NULL){  //访问左子结点  InOrder(T->lchild);  //访问根节点  Visit(T);  //访问右子结点  InOrder(T->rchild);  }  
}  
//后序遍历
void PostOrder(BiTree T){if(T != NULL){//访问左子结点PostOrder(T->lchild);//访问右子结点PostOrder(T->rchild);//访问根节点Visit(T);}
}
/* 先序遍历(非递归)
思路：访问T->data后，将T入栈，遍历左子树；遍历完左子树返回时，栈顶元素应为T，出栈，再先序遍历T的右子树。
*/
void PreOrder2(BiTree T){stack<BiTree> stack;//p是遍历指针BiTree p = T;//栈不空或者p不空时循环while(p || !stack.empty()){if(p != NULL){//存入栈中stack.push(p);//访问根节点printf("%c ",p->data);//遍历左子树p = p->lchild;}else{//退栈p = stack.top();stack.pop();//访问右子树p = p->rchild;}}//while
}
/* 中序遍历(非递归)
思路：T是要遍历树的根指针，中序遍历要求在遍历完左子树后，访问根，再遍历右子树。
先将T入栈，遍历左子树；遍历完左子树返回时，栈顶元素应为T，出栈，访问T->data，再中序遍历T的右子树。
*/
void InOrder2(BiTree T){stack<BiTree> stack;//p是遍历指针BiTree p = T;//栈不空或者p不空时循环while(p || !stack.empty()){if(p != NULL){//存入栈中stack.push(p);//遍历左子树p = p->lchild;}else{//退栈，访问根节点p = stack.top();printf("%c ",p->data);stack.pop();//访问右子树p = p->rchild;}}//while
}//后序遍历(非递归)
typedef struct BiTNodePost{BiTree biTree;char tag;
}BiTNodePost,*BiTreePost;void PostOrder2(BiTree T){stack<BiTreePost> stack;//p是遍历指针BiTree p = T;BiTreePost BT;//栈不空或者p不空时循环while(p != NULL || !stack.empty()){//遍历左子树while(p != NULL){BT = (BiTreePost)malloc(sizeof(BiTNodePost));BT->biTree = p;//访问过左子树BT->tag = 'L';stack.push(BT);p = p->lchild;}//左右子树访问完毕访问根节点while(!stack.empty() && (stack.top())->tag == 'R'){BT = stack.top();//退栈stack.pop();BT->biTree;printf("%c ",BT->biTree->data);}//遍历右子树if(!stack.empty()){BT = stack.top();//访问过右子树BT->tag = 'R';p = BT->biTree;p = p->rchild;}}//while
}
//层次遍历
void LevelOrder(BiTree T){BiTree p = T;//队列queue<BiTree> queue;//根节点入队queue.push(p);//队列不空循环while(!queue.empty()){//对头元素出队p = queue.front();//访问p指向的结点printf("%c ",p->data);//退出队列queue.pop();//左子树不空，将左子树入队if(p->lchild != NULL){queue.push(p->lchild);}//右子树不空，将右子树入队if(p->rchild != NULL){queue.push(p->rchild);}}
}
int main()
{BiTree T;CreateBiTree(T);printf("先序遍历：\n");PreOrder(T);printf("\n");printf("先序遍历(非递归)：\n");PreOrder2(T);printf("\n");printf("中序遍历：\n");InOrder(T);printf("\n");printf("中序遍历(非递归)：\n");InOrder2(T);printf("\n");printf("后序遍历：\n");PostOrder(T);printf("\n");printf("后序遍历(非递归)：\n");PostOrder2(T);printf("\n");printf("层次遍历：\n");LevelOrder(T);printf("\n");system("pause");return 0;
}

以上实例在VS2008上编译通过。

参考：http://blog.csdn.net/sjf0115/article/details/8645991


http://chatgpt.dhexx.cn/article/k0GAGEBV.shtml

相关文章

二叉树的四种遍历方法(前序遍历、中序遍历、后序遍历、层序遍历)有图有真相！！！

二叉树的四种遍历方法(前序遍历、中序遍历、后序遍历、层序遍历)有图有真相！！！

文章目录 二叉树的四种遍历方式前序遍历&#xff08;Preorder Traversal&#xff09;中序遍历&#xff08;Inorder Traversal&#xff09;后序遍历&#xff08;Postorder Traversal&#xff09;层序遍历&#xff08;Level Order Traversal&#xff09; 二叉树的四种遍历方式 相…
阅读更多...
二叉树的层次遍历算法

二叉树的层次遍历算法

前面学的二叉树的遍历是把二叉树看作3个部分&#xff1a;根&#xff0c;左子树&#xff0c;右子树&#xff0c;然后我们以此来访问3个部分 而层次遍历是把树看成从上到下的若干层&#xff1a;根结点在第一层&#xff0c;根结点的孩子在第二层&#xff0c;根结点的孩子的孩子在第…
阅读更多...
二叉树各种遍历算法

二叉树各种遍历算法

二叉树是许多算法题的常用结构&#xff0c;其遍历算法的各种变种就是各种题目。具体的顺序如下&#xff1a; 先序遍历&#xff1a;先根、后左、再右中序遍历&#xff1a;先左、后根、再右后序遍历&#xff1a;先左、后右、再根 递归版先序、中序、后序遍历 最简单、最直接的…
阅读更多...
带你图解二叉树的多种递归遍历（建议收藏！！）

带你图解二叉树的多种递归遍历（建议收藏！！）

文章目录 二叉树的构建结点类型的定义构建二叉树之间的关系 深度优先遍历前序遍历代码实现图解递归&#xff08;由于图片大小问题&#xff0c;建议用手机客户端查看&#xff0c;以下图解也是&#xff09; 中序遍历代码实现图解递归 后序遍历代码实现图解递归 广度优先遍历层序遍…
阅读更多...
二叉树遍历之图解Mirror算法(莫里斯算法)

二叉树遍历之图解Mirror算法(莫里斯算法)

144. 二叉树的前序遍历 我们写二叉树的遍历时&#xff0c;一般有两种方式&#xff0c;迭代和递归。然而还有一种神奇的算法&#xff0c;也可以作我们的二叉树递归&#xff0c;且空间复杂度为O(1)&#xff0c;要知道&#xff0c;我们迭代和递归都是需要额外栈空间的 递归和迭代网…
阅读更多...
二叉树遍历方法——前、中、后序遍历（图解）

二叉树遍历方法——前、中、后序遍历（图解）

目录 一、前序遍历 &#xff08;1&#xff09;递归版本 &#xff08;2&#xff09;非递归版本 二、中序遍历 &#xff08;1&#xff09;递归版本 &#xff08;2&#xff09;非递归版本 三、后序遍历 &#xff08;1&#xff09;递归版本 &#xff08;2&#xff09;非递归版…
阅读更多...
详细图解二叉树四种遍历(前序中序后序层次遍历)

详细图解二叉树四种遍历(前序中序后序层次遍历)

文章目录 一.前序遍历常规操作简单方法 二.中序遍历常规操作简单方法 三.后序遍历常规操作 四.层次遍历常规操作 本文中以此二叉树为例 一.前序遍历 常规操作 先根&#xff0c;再左&#xff0c;再右 确定了遍历整体结构&#xff1a; 确定了左子树中的整体结构 继续操作&…
阅读更多...
FPN细节剖析以及pytorch代码实现

FPN细节剖析以及pytorch代码实现

目录 FPN&#xff08;feature pyramid network&#xff09; 网络结构 bottleneck pytorch代码实现 公式&#xff1a;卷积层输入输出大小的计算公式 细节一&#xff1a;代码中blocks参数的含义 细节二&#xff1a;c1 c2 c3 c4 c5层尺寸分别为原图的1/2 1/4 1/8 1/16 1/32…
阅读更多...
目标检测之FPN、AugFPN、NAS-FPN

目标检测之FPN、AugFPN、NAS-FPN

针对小目标的检测有提升的文章。 未完待续~ Feature Pyramid Networks for Object Detection FPN是一种多尺度的目标检测算法。大多数目标检测算法都是采用顶层特征来做预测的&#xff0c;但是我们知道&#xff1a;低层的特征语义信息较少&#xff0c;但是位置信息丰富&#x…
阅读更多...
FPN网络和RPN网络介绍

FPN网络和RPN网络介绍

原文链接 神经网络特征提取过程中&#xff0c;一般底层特征具有良好的空间信息&#xff0c;高层的具有良好的语义信息。原来多数的object detection算法都是只采用顶层特征做预测&#xff0c;但我们知道低层的特征语义信息比较少&#xff0c;但是目标位置准确&#xff1b;高层…
阅读更多...
Neck网络 FPN + PAN 改进解读

Neck网络 FPN + PAN 改进解读

呃 这篇文章的目的在于补充一些知识以便于理解Neck部分的网络 特征提取网络 与 目标检测之间的关系 一个特征提取网络&#xff0c;假设有1000层&#xff0c;开始的特征图包含的细节信息就很多&#xff0c;而随着网络的加深&#xff0c;特征提取网络经过多次被卷积和池化操作&…
阅读更多...
FPN论文笔记

FPN论文笔记

FPN论文笔记 现在看FPN和Inception并行结构融合有点像&#xff0c;FPN上采样同时横向连接相加&#xff0c;Inception是堆叠几个感受野不同的feature&#xff0c;融合的思想有点相似。 FPN是什么&#xff1f; Feature Pyramid Networks,用于特征抽取&#xff08;feature extr…
阅读更多...
FPN算法一览

FPN算法一览

FPN应该是2017年CV顶会的优秀论文&#xff0c;基于目标检测做的研究&#xff0c;在小物体检测方面较为具有吸引力。 1.FPN 源论文&#xff1a;feature pyramid networks for object detection 参考代码&#xff1a;FPN 同时利用低层特征高分辨率和高层特征的高语义信息&…
阅读更多...
目标检测中的各种FPN

目标检测中的各种FPN

早期的目标检测算法&#xff0c;无论是一步式的&#xff0c;还是两步式的&#xff0c;通常都是在Backbone的最后一个stage&#xff08;特征图分辨率相同的所有卷积层归类为一个stage&#xff09;最后一层的特征图&#xff0c;直接外接检测头做目标检测。此种目标检测算法&#…
阅读更多...
FPN（在FasterRCNN里面是如何运用的）

FPN（在FasterRCNN里面是如何运用的）

FPN(Feature Pyramid Networks) FPN解决了什么问题&#xff1f; 答&#xff1a;FPN的提出是为了实现更好的feature maps融合&#xff0c;一般的网络都是直接使用最后一层的feature maps&#xff0c;虽然最后一层的feature maps 语义强&#xff0c;但是位置和分辨率都比较低&…
阅读更多...
深度学习之FPN+PAN

深度学习之FPN+PAN

一、FPN 检测不同尺度的物体具有挑战性&#xff0c;尤其是对于小物体&#xff0c;我们可以使用不同尺度的同一图像的金字塔来检测物体&#xff08;下左图&#xff09;但是&#xff0c;处理多尺度图像非常耗时并且内存需求太高而无法同时进行端到端训练&#xff0c;因此创建了一…
阅读更多...
FPN全解-最全最详细

FPN全解-最全最详细

这篇论文是CVPR2017年的文章&#xff0c;采用特征金字塔做目标检测&#xff0c;有许多亮点&#xff0c;特来分享。 论文&#xff1a;feature pyramid networks for object detection 论文链接&#xff1a;https://arxiv.org/abs/1612.03144 论文概述&#xff1a; 作者提出的…
阅读更多...
FPN和PAN的内容及区别

FPN和PAN的内容及区别

FPN和PAN都是用于解决在目标检测中特征金字塔网络(FPN)在多尺度检测任务上的不足的方法。下面分别详细介绍一下它们的原理和区别。 FPN FPN全称Feature Pyramid Network&#xff0c;是由FAIR在2017年提出的一种处理多尺度问题的方法。FPN的主要思路是通过构建金字塔式的特征图…
阅读更多...
深度学习之FPN和PAN

深度学习之FPN和PAN

注&#xff1a;借鉴整理&#xff0c;仅供自学&#xff0c;侵删 FPN是自顶向下&#xff0c;将高层的强语义特征传递下来&#xff0c;对整个金字塔进行增强&#xff0c;不过只增强了语义信息&#xff0c;对定位信息没有传递。PAN就是针对这一点&#xff0c;在FPN的后面添加一个自…
阅读更多...
FPN网络介绍

FPN网络介绍

目录 前言一.FPN网络二.网络创新点 前言 上一篇博文我们介绍了FCN结构&#xff0c;这篇博文我们来简答的介绍下FPN网络&#xff0c;FPN (Feature Pyramid Network) 是一种用于图像语义分割、物体检测等任务的神经网络结构。是针对目标检测提出的结构。 一.FPN网络 先来看下FP…
阅读更多...
推荐文章

Copyright @ 2022~2023