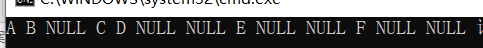目录
1、二叉树的定义及特点
2、满二叉树和完全二叉树的概念
3、二叉树的存储结构
4、创建二叉树
5、树的四种遍历方法
6、结果及其分析
1、二叉树的定义及特点
二叉树是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左孩子树和右孩子树组成的非空树;左子树和右孩子树又同样都是二叉树 。
二叉树是由m(m>=0)个节点组成的有限集合,二叉树一个节点的子节点应该为n(n<=2),并且二叉树严格区分左孩子和右孩子。
二叉树的特点:
在k层中的最大节点个数为 2^(k-1);
层数为k的树的最大节点个数为 2^k -1;
叶节点的个数比度数为2的节点的个数要多1个: n0 = n2+1总节点数为各类节点之和:n=no+n1+n2
总节点数为所有子节点数加一: n= n + 2*n2+ 1 故得: no=n2+1
2、满二叉树和完全二叉树的概念
要实现二叉树的遍历,我们还需要了解什么是满二叉树和完全二叉树:
满二叉树:深度为k (k≥1)时有2k-1个节点的二叉树。
完全二叉树:只有最下面两层有度数小于2的节点,且最下面一层的叶节点集中在最左边的若干位置上。具有n个节点的完全二叉树的深度为
(log2n)+1 或 log2(n+1)
3、二叉树的存储结构
二叉树的存储方式即可以选择顺序存储,也可以选择链式存储,但考虑到内存占用的问题,大多数情况下我们都采用链式存储,此处我们也采用链式存储进行树的遍历。
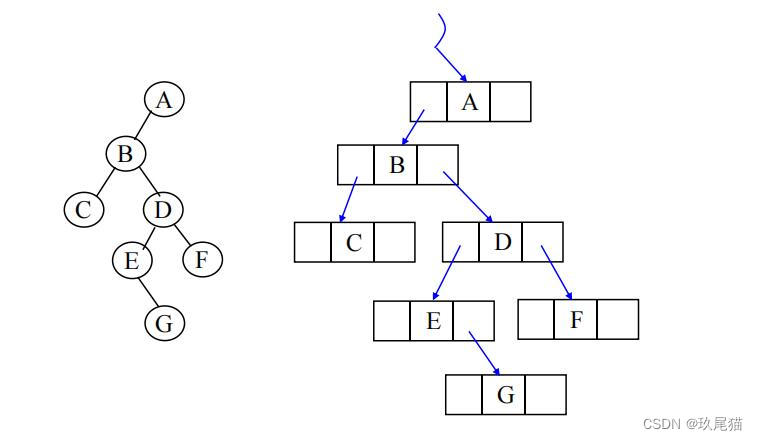
如图所示,要实现二叉树的链式存储,我们需要在结构体定义环节对每个节点的左孩子节点和右孩子节点的地址进行保存;因此结构体定义应该如下所示:
typedef char data_t;typedef struct tree
{data_t data;//存放本节点数据struct tree *l_child;//存放左孩子节点地址struct tree *r_child;//存放右孩子节点地址
}Tree;4、创建二叉树
结构体定义完成,接下来我们创建二叉树:
Tree *Create_Tree()
{Tree *root;char ch;scanf("%c", &ch);//通过输入的ch是否为特殊符号来判断该节点是否有孩子节点if(ch == '#'){ //不存在孩子节点return NULL;}else{root = (Tree *)malloc(sizeof(Tree));if(NULL == root){printf("创建失败\n");return NULL;}root->data = ch;root->l_child = Create_Tree();//存在左孩子节点,递归调用本函数,使得左孩子节点先被赋值root->r_child = Create_Tree();return root;}
}在这段代码中我们需要来看一下二叉树创建的原理:
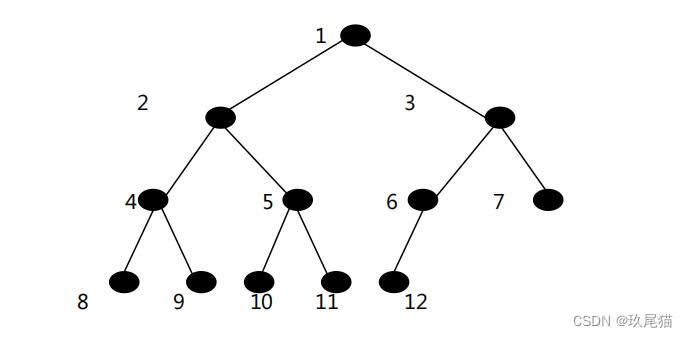
按照一般的存储逻辑,我们一般存储都是按照如下编号逐个存储,但是这样的存储方式不太适用于我们的链式存储,因此,这里我们需要使用到递归存储。
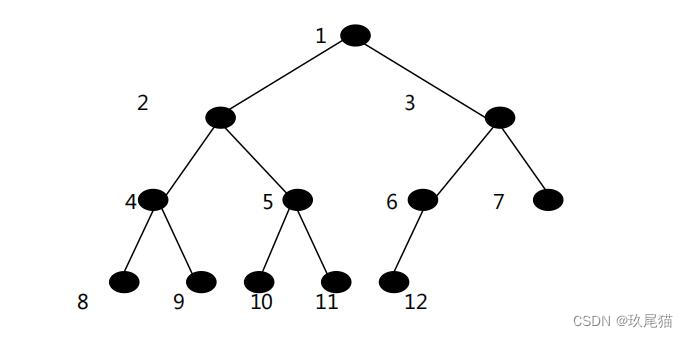
接下来,我们构思一下递归思路:
要实现递归,首先我们需要思考哪些步骤是重复多次进行的?在这里我们发现,我们每次存储时,基本上都是按照从上到下,从左到右的方式进行存储的,所以,我们此处存储数据时,可以先把根节点下面的左子树先存放完成,再存放右子树即可实现数据存储,并且,我们存放玩上一个数据之后的每一个节点都可以看做是一个根节点。这样,我们的递归思路大致就为:
1、判断一个根节点是否有孩子,如果有执行下一步,没有返回NULL
2、创建一个新的节点保存数据
3、存在左孩子节点,将左孩子节点作为下一个根节点进行操作(递归调用本函数)
4、左孩子数据存放玩,存在右孩子,将左孩子节点作为下一个根节点进行操作(递归调用本函数)
通过以上步骤之后,我们的树就建起来啦!!!
5、树的四种遍历方法
接下来,我们通过三种递归遍历输出我们的结果检查一下:
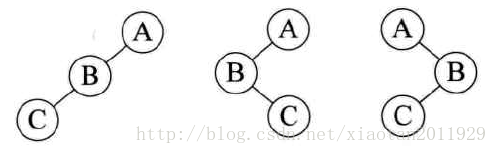
1、先序遍历(即按照根节点,左孩子树,右孩子树的顺序遍历)
void Preorder_Tree(Tree *root)
{if(NULL == root){return;}printf("%c ", root->data);//输出当前节点的数据Preorder_Tree(root->l_child);//将子节点作为下一个根节点遍历左孩子数Preorder_Tree(root->r_child);//将子节点作为下一个根节点遍历左孩子数
}2、中序遍历(即按照左孩子树,根节点,右孩子树的顺序遍历)
void Mediate_Tree(Tree *root)
{if(NULL == root){return;}Mediate_Tree(root->l_child);printf("%c ", root->data);Mediate_Tree(root->r_child);
}3、后续遍历(即按照左孩子树,右孩子树,根节点的顺序遍历)
void Post_Tree(Tree *root)
{if(NULL == root){return;}Post_Tree(root->l_child);Post_Tree(root->r_child);printf("%c ", root->data);
}4、层次遍历
void Level_Tree(Tree *tree)
{if(tree == NULL){return;}Tree *pos[N];int front, rear;//对头指针和对尾指针,用于出队和入队操作rear = N;while(rear--){pos[rear] = NULL;//全部置为空,方便后续判断}front = rear = 1;//此时为空队列,都指向第一个元素pos[front] = tree;rear++;//对尾指针偏移一位,用于存放新数据while(pos[front] != NULL){printf("%c ", pos[front]->data);if(pos[front]->l_child != NULL){pos[rear] = pos[front]->l_child;//左孩子节点入队rear++;}if(pos[front]->r_child != NULL){pos[rear] = pos[front]->r_child;//右孩子节点入队rear++;//尾指针偏移}front++;//头指针偏移一位判断下一个元素 }
}由于层次遍历涉及队列,逻辑上比较复杂,所以本期暂时不详细解释这段代码,后期会专门出一期层次遍历二叉树的教程,有兴趣的同学可以关注以下。
6、结果及其分析
接下来运行结果:

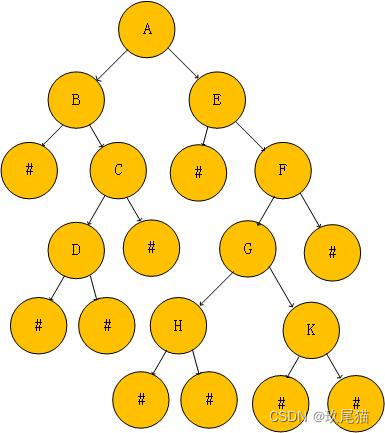
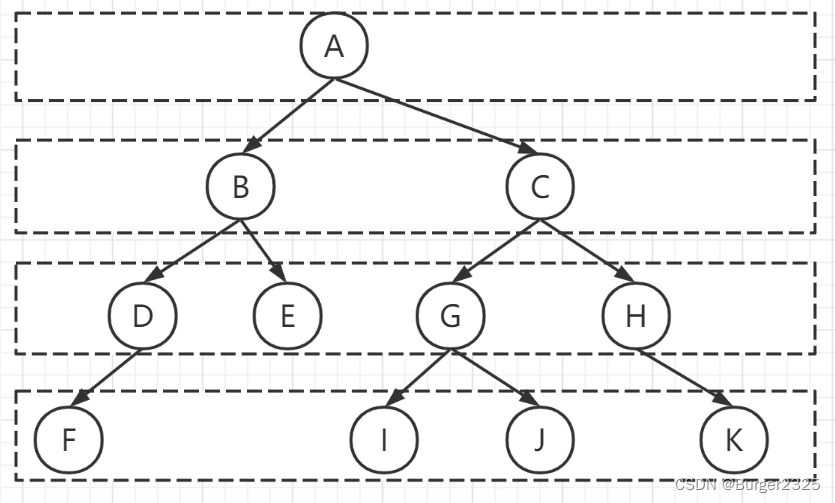
我们在输入树的内部数据时,需要使用特殊符号先将树补充为完全二叉树,即所有节点都必须有两个子节点,单个节点也需要补,如上图所示。
输入数据时从上到下,从左到右,所以依次输入AB#CD###E#FGH##K###

以上为前三种遍历方法的输出,层次输出的结果则是从最上面一层一直输出到最下面一层,输出结果正确。
以上就是本期内容,欢迎参考指正,如有不懂,评论出下期!!!