一.二叉树的遍历

1.二叉树的遍历的解释：

2.二叉树的遍历有三种递归结构

(1) 实现先序遍历：

(2) 实现中序遍历：

(3) 实现后序遍历：

(4) 二叉树的层序遍历

层序遍历代码：

二.二叉树的递归实现相关函数讲解

1.求二叉树节点个数

①错误示例1：局部变量count可以吗？—不可以

②错误示例2：局部静态变量可以吗？—不可以

③错误示例3 能过但是不安全的做法：

④正确做法：遍历思路里面的正确方法

⑤最佳做法：不用遍历的做法，思路是：子问题，

分治定义：

2.求二叉树叶子节点个数

思路1:遍历+计数

思路2:分治

3.求二叉树的第K层节点个数

4.求二叉树的深度

三.补充剩下的二叉树实现相关函数

1.二叉树查找值为x的节点

2.二叉树的销毁

3.判断二叉树是否是完全二叉树

四.完整实现：

五.层序遍历完整实现队列+二叉树

Queue.h

Queue.c

Test.c

运行结果：

一.二叉树的遍历

1.二叉树的遍历的解释：

二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉 树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

2.二叉树的遍历有三种递归结构

1. 前序遍历(Preorder Traversal 也叫先根遍历)——访问根结点的操作发生在遍历其左右子树之前。

即访问顺序为：根 -> 左子树 -> 右子树

2. 中序遍历(Inorder Traversal 也叫先根遍历)——访问根结点的操作发生在遍历其左右子树之中（间）。

即访问顺序为：左子树 -> 根 -> 右子树

3. 后序遍历(Postorder Traversal 也叫先根遍历)——访问根结点的操作发生在遍历其左右子树之后。

即访问顺序为：左子树 -> 右子树 -> 根

4.层序遍历

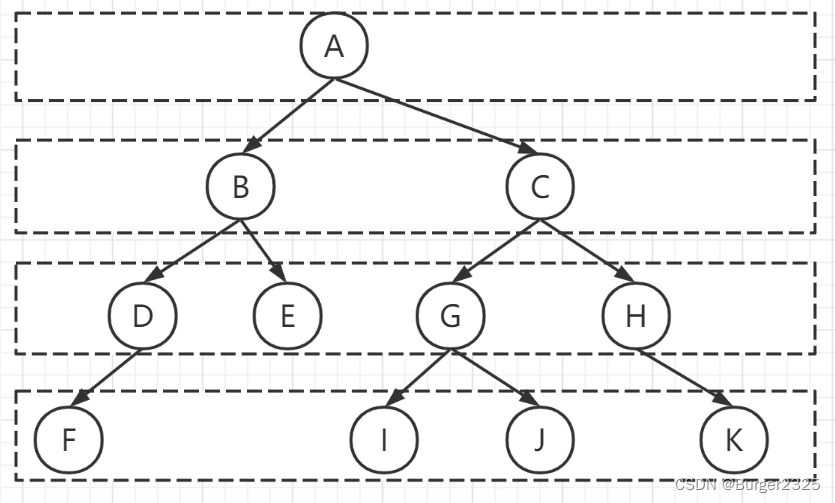
下面是3种遍历的顺序示意图：注：NULL（属于谁）

接下来我们依旧围绕此二叉树实现三种遍历：

(1) 实现先序遍历：

我们详细走一遍先序遍历，后面的中序遍历，后序遍历用图解释

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>typedef int BTDataType;typedef struct BinaryTreeNode    //定义二叉树结构体
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType data;
}BTNode;BTNode* BuyBTNode(BTDataType x)    //创建二叉树节点函数
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){printf("malloc fail\n");exit(-1);}node->data = x;node->left = node->right = NULL;return node;
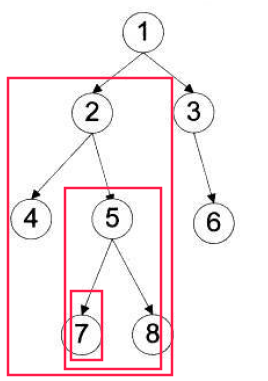
}BTNode* CreatBinaryTree()    //手动创建一个如上图所示的二叉树
{BTNode* node1 = BuyBTNode(1);BTNode* node2 = BuyBTNode(2);BTNode* node3 = BuyBTNode(3);BTNode* node4 = BuyBTNode(4);BTNode* node5 = BuyBTNode(5);BTNode* node6 = BuyBTNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}void PrevOrder(BTNode* root) {    //先序遍历函数if (root == NULL) {printf("NULL ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}

先序遍历函数解析：下图调用时有13个函数栈帧，标识即表示栈帧又表示打印顺序

栈帧1：首先传入二叉树的根root 节点1，打印1后 分为节点1左子树的先序遍历和节点1右子树的先序遍历，先沿着节点1左子树的先序遍历走到栈帧2

栈帧2：打印2后 分为节点2左子树的先序遍历和节点2右子树的先序遍历，继续沿着节点2左子树的先序遍历走到栈帧3

栈帧3：打印3后 分为节点3左子树的先序遍历和节点3右子树的先序遍历，继续沿着节点3左子树的先序遍历走到栈帧4

栈帧4：栈帧4发现节点3的左子树是NULL，则打印NULL并返回，栈帧4结束同时结束栈帧3中的PrevOrder(root->left); ，继续沿着节点3右子树的先序遍历走(即执行栈帧3中的PrevOrder(root->right);

栈帧5：栈帧5发现节点3的右子树是NULL，则打印NULL并返回，栈帧5结束同时结束栈帧3中的PrevOrder(root->right); ，此时栈帧3结束同时结束栈帧2中的PrevOrder(root->left);，继续沿着节点2右子树的先序遍历走(即执行栈帧2中的PrevOrder(root->right);）

栈帧6：栈帧6发现节点2的右子树是NULL，则打印NULL并返回，栈帧6结束同时结束栈帧2中的PrevOrder(root->right); ，此时栈帧2结束同时结束栈帧1中的PrevOrder(root->left);，继续沿着节点1右子树的先序遍历走(即执行栈帧1中的PrevOrder(root->right);）把图放中间方便观察

栈帧7：先打印4后 分为节点4左子树的先序遍历和节点4右子树的先序遍历，继续沿着节点4左子树的先序遍历走到栈帧8

栈帧8：先打印5后 分为节点5左子树的先序遍历和节点5右子树的先序遍历，继续沿着节点5左子树的先序遍历走到栈帧9

栈帧9：栈帧9发现节点5的左子树是NULL，则打印NULL并返回，栈帧9结束同时结束栈帧8中的PrevOrder(root->left); ，继续沿着节点5右子树的先序遍历走(即执行栈帧8中的PrevOrder(root->right);

栈帧10：栈帧10发现节点5的右子树是NULL，则打印NULL并返回，栈帧10结束同时结束栈帧8中的PrevOrder(root->right); ，此时栈帧8结束同时结束栈帧7中的PrevOrder(root->left);，继续沿着节点4右子树的先序遍历走(即执行栈帧7中的PrevOrder(root->right);）

栈帧11：先打印6后 分为节点6左子树的先序遍历和节点6右子树的先序遍历，继续沿着节点6左子树的先序遍历走到栈帧12

栈帧12：栈帧9发现节点6的左子树是NULL，则打印NULL并返回，栈帧12结束同时结束栈帧11中的PrevOrder(root->left); ，继续沿着节点6右子树的先序遍历走(即执行栈帧11中的PrevOrder(root->right);

栈帧13：栈帧13发现节点6的右子树是NULL，则打印NULL并返回，栈帧13结束同时结束栈帧11中的PrevOrder(root->right); ，此时栈帧11结束同时结束栈帧7中的PrevOrder(root->right);，栈帧7结束同时结束栈帧1中的PrevOrder(root->right); ，此时栈帧1结束同时结束整个递归循环

(2) 实现中序遍历：

void InOrder(BTNode* root) {if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}

看图即可，过程跟先序一样，红色的数字是传入的节点数，蓝色数字表示打印顺序：

(3) 实现后序遍历：

void PostOrder(BTNode* root) {if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}

看图即可，过程跟先序一样，仍然是红色数字是传入的节点数，蓝色数字表示打印顺序：

(4) 二叉树的层序遍历

层序遍历是一层一层遍历二叉树，例如上面的这个树，打印后就是：1 2 4 3 5 6

思路：创建一个队列（先进先出的单链表）借助队列先进先出的性质。上一层的节点出的时候，带下一层的节点进去。

特别注意的是：如果你只是把节点的值放进队列，那么打印并pop完这个值后将无法找到他的孩子，所以我们必须把整个节点都入进队列，

因此需要把Queue.h中的 typedef int QDataType; 修改为 typedef struct BinaryTreeNode* QDataType; 但是struct BinaryTreeNode 这个结构体是在Test.c中定义的，那么Queue.h中的 typedef struct BinaryTreeNode* QDataType; 将无法找到此结构体，那我们想：可以把Test.c中的 #include"Queue.h" ，放到定义 struct BinaryTreeNode 结构体的后面，当预处理时 #include"Queue.h" 被代码替换，

#include"Queue.h" 中的 typedef struct BinaryTreeNode* QDataType; 通过向上找就可以找到定义的结构体，这样总没错了吧？ ——还是有错，因为不仅Test.c使用 QDataType，Queue.c也要使用QDataType，上面的操作仅仅只是让Test.c可以正常使用了，所以我们不如直接在Queue.h中的typedef struct BinaryTreeNode* QDataType; 前添上结构体声明 struct BinaryTreeNode; ，这样两个.c文件就都可以找到此结构体了。（在Test.c中我们定义结构体：

typedef struct BinaryTreeNode
{
   struct BinaryTreeNode* left;
   struct BinaryTreeNode* right;
   BTDataType data;
}BTNode; 但是结构体声明中我们并不能直接声明 BTNode; ，还是要声明完整结构体名称，即;

）

整个过程：下面的二叉树，先把节点1放入队列（队列状态：1），打印并pop 节点1，随后把它的孩子放入队列，他的孩子正好就是下一层的前两个节点节点2 和节点4（队列状态：2 4）；

打印并pop 节点2（队列状态：4），随后把它的孩子节点3放入队列，他的孩子正好就是下一层的前一个节点节点3 右树为空就不用做事情；（队列状态：4 3）

该节点4了，打印并pop 节点4（队列状态：3），随后把它的孩子节点5，6放入队列，他的孩子正好就是下一层的第二个和第三个节点；（队列状态：3 5 6）

该节点3了，打印并pop 节点3（队列状态：5 6），发现它的孩子都是NULL，NULL节点不用放，不用做任何事情；（队列状态：5 6）

该节点5了，打印并pop 节点5（队列状态：6），发现它的孩子都是NULL，NULL节点不用放，不用做任何事情；（队列状态：6）

该节点6了，打印并pop 节点6（队列状态：NULL），发现它的孩子都是NULL，NULL节点不用放，不用做任何事情；（队列状态：NULL）

队列空，则结束！（可以看下面的动态图演示层序过程）

层序遍历代码：

#include"Queue.h"
//创建二叉树等工程请在本文章 序号五 完整代码看......void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root)                //根节点若不是NULL，将根节点入队列-开始{QueuePush(&q, root);}while (!QueueEmpty(&q))    //队列不为空时{BTNode* front = QueueFront(&q);  //获得队列第一个元素QueuePop(&q);                   //获得此元素后就可以直接pop扔掉了printf("%d ", front->data);    //打印队列第一个元素if (front->left)               //左孩子若不是NULL，将左孩子入队列{QueuePush(&q, front->left);}if (front->right)              //右孩子若不是NULL，将右孩子入队列{QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}int main()
{BTNode* tree = CreatBinaryTree();LevelOrder(tree);	//层序遍历return 0;
}

二.二叉树的递归实现相关函数讲解

1.求二叉树节点个数

我们先手动创建一个上图所示的二叉树：

typedef int BTDataType;
typedef struct BTNode
{struct BTNode* left;struct BTNode* right;BTDataType data;
}BTNode;BTNode* BuyBTNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){printf("malloc fail\n");exit(-1);}node->data = x;node->left = node->right = NULL;return node;
}BTNode* CreatBinaryTree()
{BTNode* node1 = BuyBTNode(1);BTNode* node2 = BuyBTNode(2);BTNode* node3 = BuyBTNode(3);BTNode* node4 = BuyBTNode(4);BTNode* node5 = BuyBTNode(5);BTNode* node6 = BuyBTNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}

下面代码都是在此基础上进行的

受前面的二叉树遍历的引导，我们不禁思考：若求二叉树节点个数，只要把每个非空节点的打印改成计数不就可以了吗？思想：遍历+计数，那直接上手写代码是非常容易考虑不全的，我们需要一步一步探索正确答案并纠正~

①错误示例1：局部变量count可以吗？—不可以

int BTreeSize(BTNode* root)
{int count = 0;if (root == NULL)return count;++count;BTreeSize(root->left);BTreeSize(root->right);return count;
}

我们直接把打印改成计数后，写出这样的代码。这样是有问题的：count作为局部变量，在每一次递归调用自己时都会刷新为0，然后再计数就没有意义了。

②错误示例2：局部静态变量可以吗？—不可以

 //多次调用会有问题，没办法每次初始化为0
int BTreeSize(BTNode* root)
{static int count = 0;if (root == NULL)return count;++count;BTreeSize(root->left);BTreeSize(root->right);return count;
}int main()
{BTNode* tree = CreatBinaryTree();printf("size:%d\n", BTreeSize(tree));printf("size:%d\n", BTreeSize(tree));    //调用多次就会叠加，就错了printf("size:%d\n", BTreeSize(tree));return 0;
}

我们可能会想到用static修饰的静态变量就可以计数了，但是这样也是有问题的，当你多次调用BTreeSize 这个求二叉树节点个数的函数时，第一次静态变量count已经加到6，再调用 BTreeSize(tree) 时count的初始值就是6，第二次打印节点个数就是12，第三次就是18，会叠加，所以不行。

③错误示例3 能过但是不安全的做法：

那我用个全局变量count计数，每次count置0行吗？此时函数也没有返回值了

//线程安全的问题，这个以后linux学了大家就知道了
int count = 0;
void BTreeSize(BTNode* root)
{if (root == NULL)return;++count;BTreeSize(root->left);BTreeSize(root->right);
}int main()
{BTNode* tree = CreatBinaryTree();count = 0;BTreeSize(tree);printf("size:%d\n", count);count = 0;BTreeSize(tree);printf("size:%d\n", count);count = 0;BTreeSize(tree);printf("size:%d\n", count);return 0;
}

答案是不行~全局变量同时被调用，同时count++，会有线程安全的问题，会使count错乱，这里作为了解，反正尽量不用全局变量。

④正确做法：遍历思路里面的正确方法

思想：遍历+计数用这种思路，这里要用传址调用并且每次使用次函数时也要手动把count给成0。

void BTreeSize(BTNode* root, int* pcount)
{if (root == NULL){return 0;}(*pcount)++;BTreeSize(root->left, pcount);BTreeSize(root->right, pcount);
}int main()
{BTNode* tree = CreatBinaryTree();int count1 = 0;BTreeSize(tree, &count1);printf("size:%d\n", count1);int count2 = 0;BTreeSize(tree, &count2);printf("size:%d\n", count2);return 0;
}

⑤最佳做法：不用遍历的做法，思路是：子问题，

1、空树，最小规模子问题，节点个数返回0
2、非空，左子树节点个数+右子树节点个数+1 (自己)

传入根节点root，如果根节点root是NULL就无节点，返回0；如果根节点root不是NULL就化为两个子问题计算左树节点数和右树节点数相加，并加上1(自己)。

int BTreeSize (BTNode* root)
{return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1;
}
int main()
{BTNode* tree = CreatBinaryTree();printf("%d ", BTreeSize (tree));return 0;
}

其实这种子问题的思想也叫作分治思想：

分治定义：

把复杂的问题，分成更小规模的子问题，子问题再分成更小规模的子问题。直到子问题不可再分割，直接能出结果。

2.求二叉树叶子节点个数

思路1:遍历+计数

遍历整个二叉树，遇到叶子就++，当root为空时就返回。

void BTreeLeafSize1(BTNode* root,int* pcount)
{if (root == NULL)return;if (root->left == NULL && root->right == NULL){(*pcount)++;}BTreeLeafSize1(root->left, pcount);BTreeLeafSize1(root->right, pcount);
}
int main()
{BTNode* tree = CreatBinaryTree();int count = 0;BTreeLeafSize1(tree,&count);printf("BTreeLeafSize1:%d\n ", count);return 0;
}

思路2:分治

把二叉树叶子个数分为左子树叶子个数+右子树叶子个数，如果root是叶子就返回1，是空就返回0

int BTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}
int main()
{BTNode* tree = CreatBinaryTree();printf("BTreeLeafSize:%d\n", BTreeLeafSize(tree));return 0;
}

3.求二叉树的第K层节点个数

思想:
1、空树，返回0
2、非空，且k== 1,返回1
3、非空，且k> 1,转换成左子树k-1层节点个数+右子树k-1层节点个数

int BTreeKLevelSize(BTNode* root,int k)
{assert(k>=1);if (root == NULL)return 0;if (k == 1)return 1;return BTreeKLevelSize(root->left, k - 1) + BTreeKLevelSize(root->right, k - 1);
}int main()
{BTNode* tree = CreatBinaryTree();printf("BTreeKLevelSize:%d\n ", BTreeKLevelSize(tree, 2));return 0;
}

4.求二叉树的深度

分治思想:比较左子树高度和右子树高度，返回大的那个子树的深度+1，当节点是NULL时返回0，当左右子树都为NULL时，0和0比较后+1，即返回1（因为就自己一层）

int BTreeDepth(BTNode* root)
{if (root == NULL)return 0;int leftDepth = BTreeDepth(root->left);int rightDepth = BTreeDepth(root->right);return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}int main()
{BTNode* tree = CreatBinaryTree();printf("BTreeDepth:%d\n", BTreeDepth(tree));return 0;
}

不懂的请看完整递归图：

三.补充剩下的二叉树实现相关函数

1.二叉树查找值为x的节点

查找函数思路很简单：从根节点开始，如果节点为NULL就返回NULL，如果节点值=x就返回这个节点地址，继续向下判断孩子，如果这个节点的左孩子不为空，说明找到了，找到就返回左孩子；如果右孩子不为空，就返回右孩子；当都为空，走到最后，说明没找到，没找到就返回NULL。

// 二叉树查找值为x的节点
BTNode* BTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)    //如果节点为空就返回NULLreturn NULL;if (root->data == x)    //如果节点值=x就返回这个节点return root;BTNode* ret1 = BTreeFind(root->left, x);    if (ret1)    如果节点的左孩子不为空，说明找到了，找到就返回左孩子{return ret1;}BTNode* ret2 = BTreeFind(root->right, x);if (ret2)    //如果节点的右孩子不为空，说明找到了，找到就返回右孩子{return ret2;}return NULL;    //当走到这里的时候，说明没找到，没找到就返回NULL
}int main()
{BTNode* tree = CreatBinaryTree();for (int i = 1; i <= 7; ++i){printf("Find:%d,%p\n", i, BTreeFind(tree, i));}BTNode* ret = BTreeFind(tree, 5);if (ret){ret->data = 50;}return 0;
}

运行结果：

2.二叉树的销毁

void BTreeDestory(BTNode* root)
{if (root == NULL){return;}BTreeDestory(root->left);BTreeDestory(root->right);free(root);
}

销毁要一个节点一个节点销毁，如果你上来就free了根节点，那下面的节点都找不到了，所以应该先free左右孩子节点，最后free根节点，因此应该用后序遍历的方式free每一个节点，左孩子->右孩子->根依次free。如果是空节点就不用free，直接返回即可。

3.判断二叉树是否是完全二叉树

void BTreeDestroy(BTNode* root)
{if (root == NULL)return ;BTreeDestroy( root->left );BTreeDestroy( root->right );free(root);
}//2.判断二叉树是否是完全二叉树
bool BTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)        // 3.如果二叉树不为空，先放根节点QueuePush(&q, root);while (!QueueEmpty(&q))   //4.当队列不空就层序遍历{BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)    //5.看队头数据是否是空，是空就break进入下面检查后面是否有非空break;QueuePush(&q, front->left);    //6.走到这说明没遇到空节点，继续层序遍历QueuePush(&q, front->right);}while (!QueueEmpty(&q))    //7.走到这说明已经遇到空节点，开始检查后面是否有非空，继续层序遍历找非空节点{BTNode* front = QueueFront(&q);QueuePop(&q);if (front)    // 8.空节点后面出到非空节点，那么说明不是完全二叉树{QueueDestory(&q);  //9.不是完全二叉树就返回false，返回前记的销毁队列，否则内存泄漏return false;}}//10.走到这说明第一次遇到空节点后，后面都是空节点，说明是完全二叉树，是就返回true，返回前要销毁队列QueueDestory(&q); return true;
}int main()
{BTNode* tree = CreatBinaryTree();    // 1.创建上图所示的二叉树printf("%d ",BTreeComplete(tree));    // 11.打印返回的布尔值BTreeDestroy(tree);       // 12.对二叉树销毁tree = NULL;return 0;
}

整体思路：

1、层序遍历，空节点也进队列
2、出到空节点以后，出队列中所有数据，如果全是空，就是完全二叉树，如果有非空，就不是
(详情请见上面代码注释过程)

运行结果就是0

四.完整实现：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<time.h>
#include<stdlib.h>
#include<assert.h>typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;BTNode* BuyBTNode(BTDataType x)//————————————————————————————————————————————————————
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){printf("malloc fail\n");exit(-1);}node->data = x;node->left = node->right = NULL;return node;
}//创建一个二叉树—————————————————————————————————————————————————————————
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyBTNode(1);BTNode* node2 = BuyBTNode(2);BTNode* node3 = BuyBTNode(3);BTNode* node4 = BuyBTNode(4);BTNode* node5 = BuyBTNode(5);BTNode* node6 = BuyBTNode(6);//BTNode* node7 = BuyBTNode(7);node1->left = node2;node1->right = node4;node2->left = node3;//node2->right = node7;node4->left = node5;node4->right = node6;return node1;
}// 二叉树销毁————————————————————————————————————————————————————————————
void BTreeDestory(BTNode* root)
{if (root == NULL){return;}BTreeDestory(root->left);BTreeDestory(root->right);free(root);
}// 二叉树节点个数(2种)————————————————————————————————————————————————————
void BTreeSize1(BTNode* root, int* pcount)
{if (root == NULL){return 0;}(*pcount)++;BTreeSize(root->left, pcount);BTreeSize(root->right, pcount);
}int BTreeSize(BTNode* root)
{return root == NULL ? 0 : BTreeSize(root->left) + BTreeSize(root->right) + 1;
}// 二叉树叶子节点个数(2种)————————————————————————————————————————————————————
int BTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;return BTreeLeafSize(root->left) + BTreeLeafSize(root->right);
}void BTreeLeafSize1(BTNode* root, int* pcount)
{if (root == NULL)return;if (root->left == NULL && root->right == NULL){(*pcount)++;}BTreeLeafSize1(root->left, pcount);BTreeLeafSize1(root->right, pcount);
}// 二叉树第k层节点个数————————————————————————————————————————————————————————————
int BTreeKLevelSize(BTNode* root, int k)
{assert(k >= 1);if (root == NULL)return 0;if (k == 1)return 1;return BTreeKLevelSize(root->left, k - 1) + BTreeKLevelSize(root->right, k - 1);
}
// 二叉树的深度
int BTreeDepth(BTNode* root)
{if (root == NULL)return 0;int leftDepth = BTreeDepth(root->left);int rightDepth = BTreeDepth(root->right);return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}// 二叉树查找值为x的节点——————————————————————————————————————————————————————————
BTNode* BTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* ret1 = BTreeFind(root->left, x);if (ret1){return ret1;}BTNode* ret2 = BTreeFind(root->right, x);if (ret2){return ret2;}return NULL;
}// 二叉树前序遍历 ———————————————————————————————————————————————————————————————
void PrevOrder(BTNode* tree)	//前序遍历	根-左子树-右子树
{if (tree == NULL){printf("NULL ");return;}printf("%d ", tree->data);PrevOrder(tree->left);PrevOrder(tree->right);
}// 二叉树中序遍历———————————————————————————————————————————————————————————————
void InOrder(BTNode* root) {if (root == NULL) {printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}// 二叉树后序遍历———————————————————————————————————————————————————————————————
void PostOrder(BTNode* root) {if (root == NULL) {printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}// 层序遍历—————————————————————————————————————————————————————————————————————
void BinaryTreeLevelOrder(BTNode* root); //因为要用到队列，在最后单独列出
// 判断二叉树是否是完全二叉树—————————————————————————————————————————————————————
bool BTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)break;QueuePush(&q, front->left);QueuePush(&q, front->right);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);// 空后面出到非空，那么说明不是完全二叉树if (front){QueueDestory(&q);return false;}}QueueDestory(&q);return true;
}int main()
{BTNode* tree = CreatBinaryTree();//int count = 0;//BTreeSize1(tree ,&count);//printf("%d ", count);printf("BTreeSize:%d\n", BTreeSize(tree));printf("BTreeLeafSize:%d\n", BTreeLeafSize(tree));int count = 0;BTreeLeafSize1(tree, &count);printf("BTreeLeafSize1:%d\n", count);printf("BTreeKLevelSize:%d\n", BTreeKLevelSize(tree, 2));BTreeDepth(tree);printf("BTreeDepth:%d\n", BTreeDepth(tree));BTreeFind(tree, 6);printf("BTreeFind:%d", BTreeFind(tree, 6)->data);printf("%d ",BTreeComplete(tree));   BTreeDestroy(tree);       //对二叉树销毁tree = NULL;return 0;
}

五.层序遍历完整实现队列+二叉树

Queue.h

#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>struct BinaryTreeNode;
typedef struct BinaryTreeNode* QDataType;typedef struct QueueNode
{QDataType data;struct QueueNode* next;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;
}Queue;void QueueInit(Queue* pq);void QueueDestory(Queue* pq);void QueuePush(Queue* pq, QDataType x);void QueuePop(Queue* pq);bool QueueEmpty(Queue* pq);size_t QueueSize(Queue* pq);QDataType QueueFront(Queue* pq);QDataType QueueBack(Queue* pq);

Queue.c

#define _CRT_SECURE_NO_WARNINGS
#include"Queue.h"void QueueInit(Queue* pq)
{assert(pq);pq->head = NULL;pq->tail = NULL;
}void QueueDestroy(Queue* pq)			//复盘！！！
{assert(pq);QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head =pq->tail = NULL;}void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));assert(newnode);newnode->next = NULL;newnode->data = x;if (pq->tail == NULL){assert(pq->head==NULL);pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;			//写的时候漏了！！！}
}void QueuePop(Queue* pq)
{assert(pq);assert(pq->head && pq->tail);if (pq->head == pq->tail){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* next = pq->head->next;free(pq->head);pq->head = next;}
}bool QueueEmpty(Queue* pq)
{assert(pq);//return pq->head == NULL && pq->tail == NULL;return pq->head == NULL;
}size_t QueueSize(Queue* pq)
{assert(pq);size_t size = 0;QNode* cur = pq->head;while (cur){size++;cur = cur->next;}return size;
}QDataType QueueFront(Queue* pq)
{assert(pq);assert(pq->head);return pq->head->data;
}QDataType QueueBack(Queue* pq)
{assert(pq);assert(pq->tail);return pq->tail->data;}

Test.c

#define _CRT_SECURE_NO_WARNINGS
#include"Queue.h"typedef int BTDataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BTDataType data;
}BTNode;BTNode* BuyBTNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){printf("malloc fail");exit(-1);}node->data = x;node->left = node->right = NULL;return node;
}
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyBTNode(1);BTNode* node2 = BuyBTNode(2);BTNode* node3 = BuyBTNode(3);BTNode* node4 = BuyBTNode(4);BTNode* node5 = BuyBTNode(5);BTNode* node6 = BuyBTNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}//思路:
//1、先把跟入队列，借助队列，先进先出的性质。
//2、上 - -层的节点出的时候,带下一层的节点进去。void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}
int main()
{BTNode* tree = CreatBinaryTree();LevelOrder(tree);	//层序遍历return 0;
}