二叉树遍历（图解）

article/2025/9/22 6:16:01

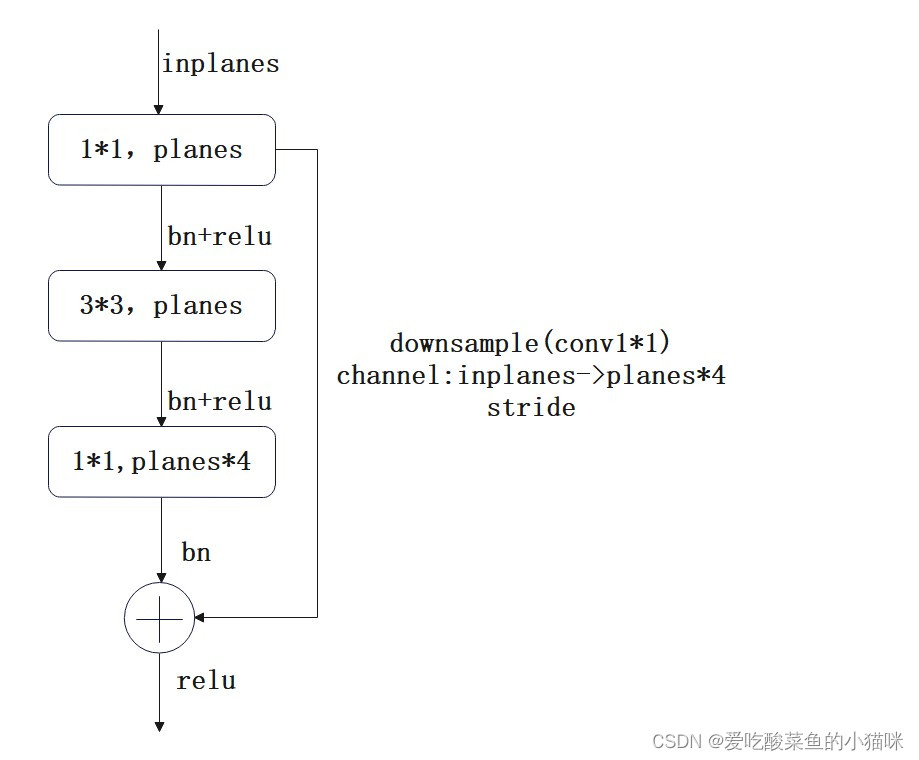
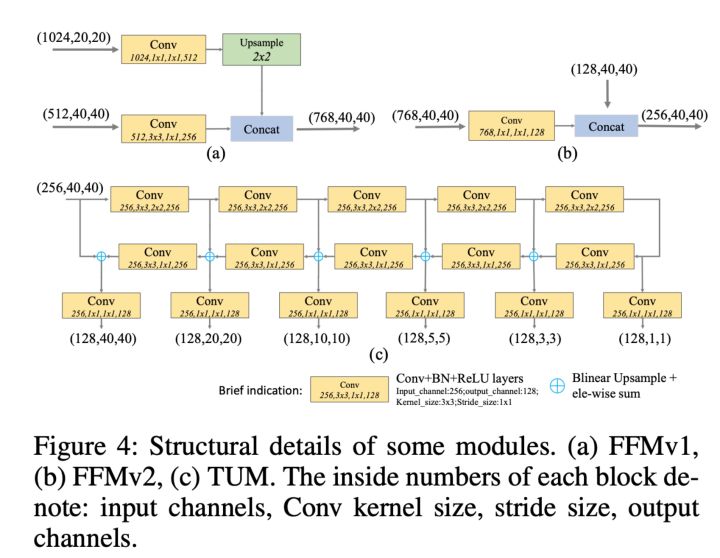
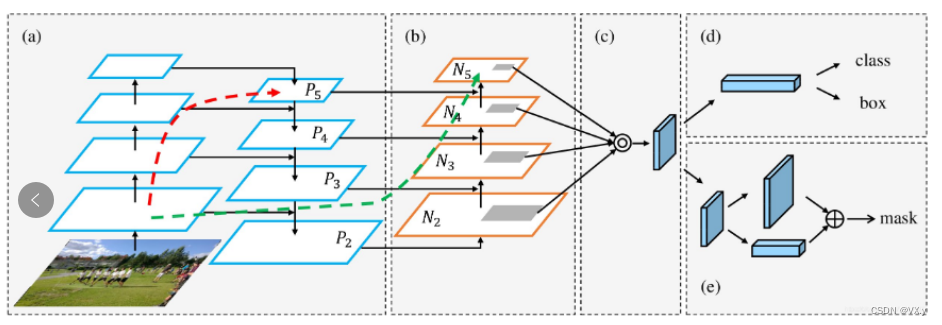
二叉树的顺序存储结构就是用一维数组存储二叉树中的节点，并且节点的存储位置，也就是数组的下标要能体现节点之间的逻辑关系。—–>一般只用于完全二叉树
链式存储—–>二叉链表
定义： lchild | data | rchild（两个指针域，一个数据域）

typedef struct Node {ElemType data;struct Node *lchild, *rchild;
}BiTnode,* BiTree;

注意点：
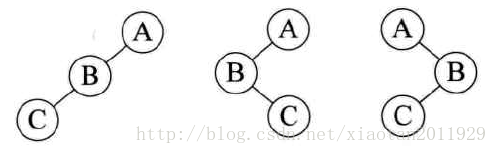
1）已知 前序遍历序列 和 中序遍历序列，可以唯一确定一颗二叉树
2）已知 中序遍历序列和 后序遍历序列，可以唯一确定一颗二叉树
而已知前序和后序是不能确定一颗二叉树的

二叉树的遍历：是指从根节点出发，按照某种次序依次访问二叉树中的所有节点，使得每个节点被访问一次且仅被访问一次。

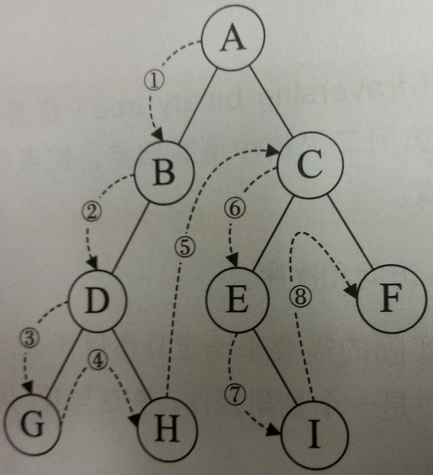
1、前序遍历：根-左-右
这里写图片描述

代码：

void PreOrder(BiTree T) /*先序遍历: 根-左-右*/
{if(T != NULL){Visit(T);   /*访问根节点*/PreOrder(T->lchild);  /*访问左子节点*/PreOrder(T->rchild);  /*访问右子节点*/}
}

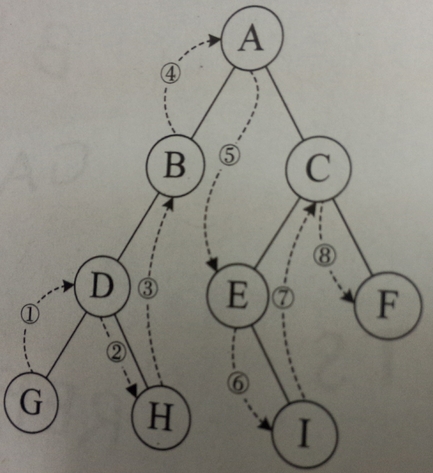
2、中序遍历：左-根-右
这里写图片描述

代码：

void InOrder(BiTree T)/*中序遍历：左-根-右*/
{if(T != NULL){InOrder(T->lchild);  //左Visit(T);            //根InOrder(T->rchild);  //右}
}

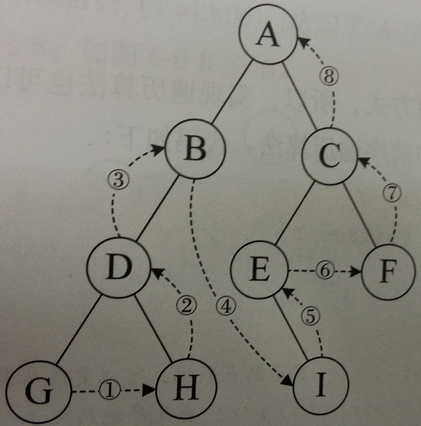
3、后序遍历：左-右-根
这里写图片描述

代码：

void PostOrder(BiTree T)/*后序遍历：左-右-根*/
{if(T != NULL){PostOrder(T->lchild);  //左PostOrder(T->rchild);  //右Visit(T);              //根}
}

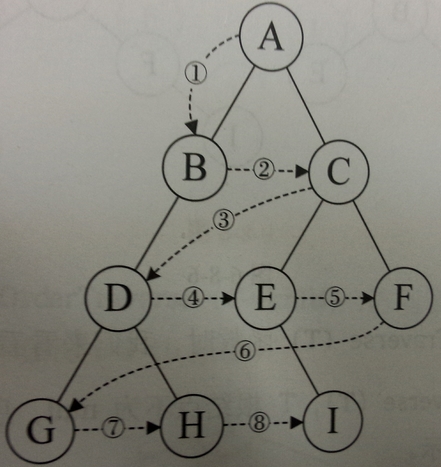
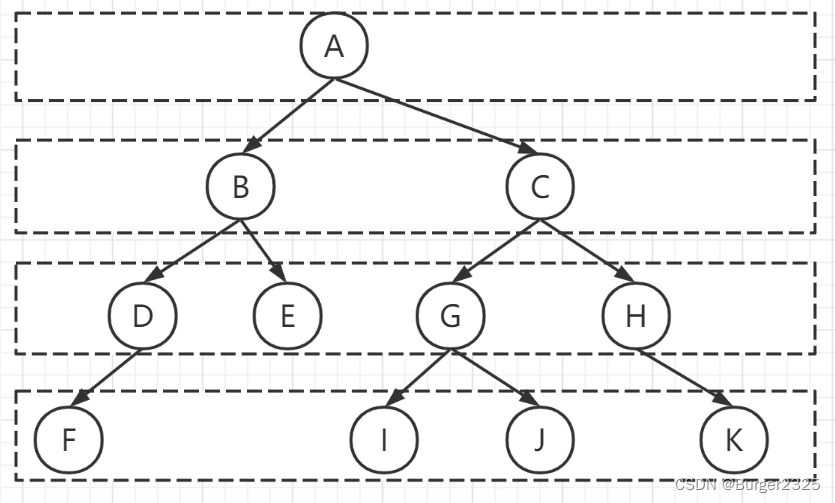
4、层序遍历：从根节点出发，依次访问左右孩子结点，再从左右孩子出发，依次它们的孩子结点，直到节点访问完毕
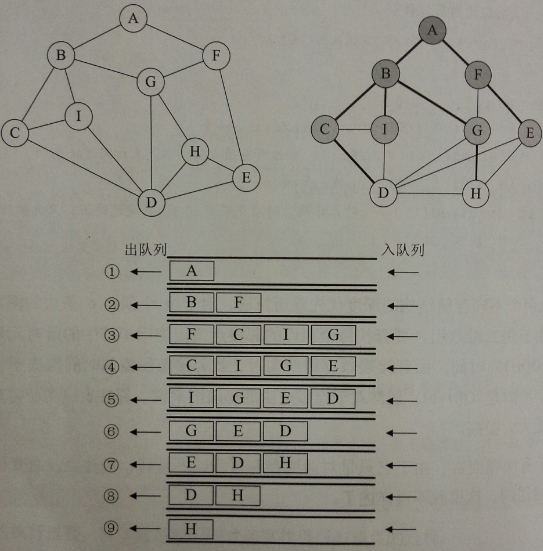
这里写图片描述

代码：该程序用到了队列的思想，可以参考下图理解
（该图为展示的是 图的广度优先遍历示意图，应用的就是层序遍历的思想）

/*层序遍历 思路：按从左至右的顺序来逐层访问每个节点，层序遍历的过程需要队列*/
void LevelOrder(BiTree T)
{BiTree p = T;queue<BiTree> queue;         /*队列*/queue.push(p);               /*根节点入队*/while(!queue.empty())        /*队列不空循环 */{p = queue.front();       /*对头元素出队*///printf("%c ",p->data); /*访问p指向的结点*/cout << p->data << " ";queue.pop();             /*退出队列*/if(p->lchild != NULL){   /*左子树不空，将左子树入队*/queue.push(p->lchild);}if(p->rchild != NULL){   /*右子树不空，将右子树入队*/queue.push(p->rchild);}}
}