一、多线程实现方式

1.1 Thread实现

继承Thread类并重写它的run方法。之后创建这个子类的对象并调用start()方法。下面直接上代码:

/**
*描述
* @author cy
* @date 2021-06-09
* @return
**/
public class TreadTest  extends  Thread{public static void main(String[] args) {//创建两个线程TreadTest thread1 = new TreadTest();TreadTest thread2 = new TreadTest();thread1.start();thread2.start();}@Overridepublic void run() {for (int i = 0;i < 100;i++){//分别打印线程名称和iSystem.out.println("threadName:"+Thread.currentThread()+"；i="+i);}}
}

输出结果可以看到两个线程交替打印。线程启动成功。

1.2 Runnable实现

Runnable的实现方式是实现其接口,下面请看具体的实现代码

/*** @author  cy* @date  2021-06-09*@deprecated  Runnable实现多线程*/
public class RunnableDemoTest {public static void main(String[] args) {//新建两个线程RunnableDemoTest1 r =  new RunnableDemoTest1();new Thread(r).start();new  Thread(r).start();}/*** 通过runnable 方式实现多线程*/
static class  RunnableDemoTest1  implements  Runnable{@Overridepublic void run() {for (int i = 0 ;i < 5 ;i++)System.out.println("threadName:"+Thread.currentThread()+"；i="+i);}
}
}

从输出结果中我们可以看到两个线程交替打印。线程启动成功。

二、多线程的使用场景

1.多线程使用场景

1.1 多线程应该最多的场景：

web服务器本身； 各种专用服务器（如游戏服务器）；

1.2多线程的常见应用场景：

1、后台任务，例如：定时向大量（100w以上）的用户发送邮件； 2、异步处理，例如：发微博、记录日志等； 3、分布式计算

2.多线程小案列

2.1 多线程计算

计算一亿个数字之和，在没有学习多线程之前，也是可以实现的，我们可以通过循环一亿次进行累加，最后得出结果。
代码如下：

package trhead;import java.util.Random;/*** 计算一亿个数之和*/
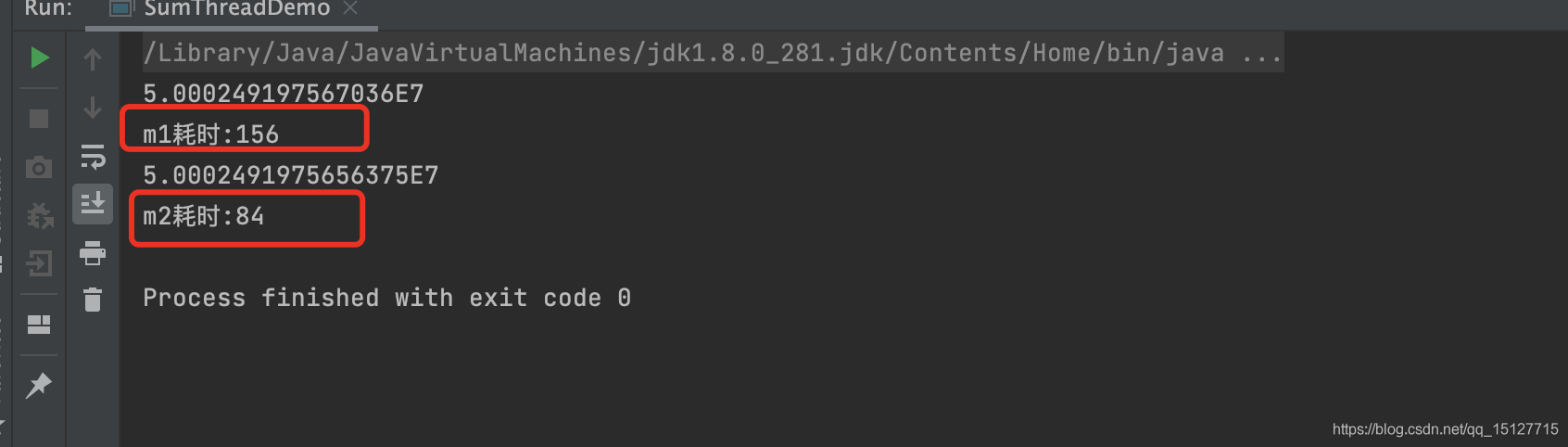
public class SumThreadDemo {private static double [] nums = new double[1_0000_0000];private static Random r  =  new Random();private static  double  result = 0.0,result1 = 0.0,result2 = 0.0;static {for (int i =0;i < nums.length ; i++){nums[i] = r.nextDouble();}}public static void main(String[] args) throws InterruptedException {SumThreadDemo.m1();SumThreadDemo.m2();}/*** 使用单线程计算*/private  static  void m1(){long startTime = System.currentTimeMillis();for (int i = 0;i < nums.length;i++){result += nums[i];}System.out.println(result);long endTime = System.currentTimeMillis();long countTime = endTime - startTime;System.out.println("m1耗时:"+countTime);}/*** 使用多线程计算*/private  static  void m2() throws InterruptedException {Thread thread1 =   new Thread(()->{for (int i = 0;i < nums.length/2;i++){result1 += nums[i];}});Thread thread2 =   new Thread(()->{for (int i = nums.length/2;i < nums.length;i++){result2 += nums[i];}});long startTime = System.currentTimeMillis();thread1.start();thread2.start();thread1.join();thread2.join();System.out.println(result1+ result2);long endTime = System.currentTimeMillis();long countTime = endTime - startTime;System.out.println("m2耗时:"+countTime);}}

从输出结果中可以观察出，两个线程计算结果比单个线程快了将近两倍。如果实际应用中有这种场景，大家可以使用多线程实现。

2.2 多线程实现卖票小程序

某电影院正在上映某大片，共5张票，而他又有3个售票窗口售票，请设计一个程序模拟该电影院售票。

多线程实现方式1:

package trhead;/**
*描述*  某电影院正在上映某大片，共5张票，* 而他又有3个售票窗口售票，请设计一个程序模拟该电影院售票。
* @author cy
* @date 2021-06-09
* @return
**/
public class TicketTreadTest extends  Thread{//设置票数private  int ticket = 5;public static void main(String[] args) {//创建两个线程TicketTreadTest thread1 = new TicketTreadTest();TicketTreadTest thread2 = new TicketTreadTest();TicketTreadTest thread3 = new TicketTreadTest();thread1.start();thread2.start();thread3.start();}@Overridepublic void run() {while(true){//分别打印线程名称 和 ticket 数System.out.println("threadName:"+Thread.currentThread()+"；ticket="+ticket--);if(ticket < 0){break;}}}
}

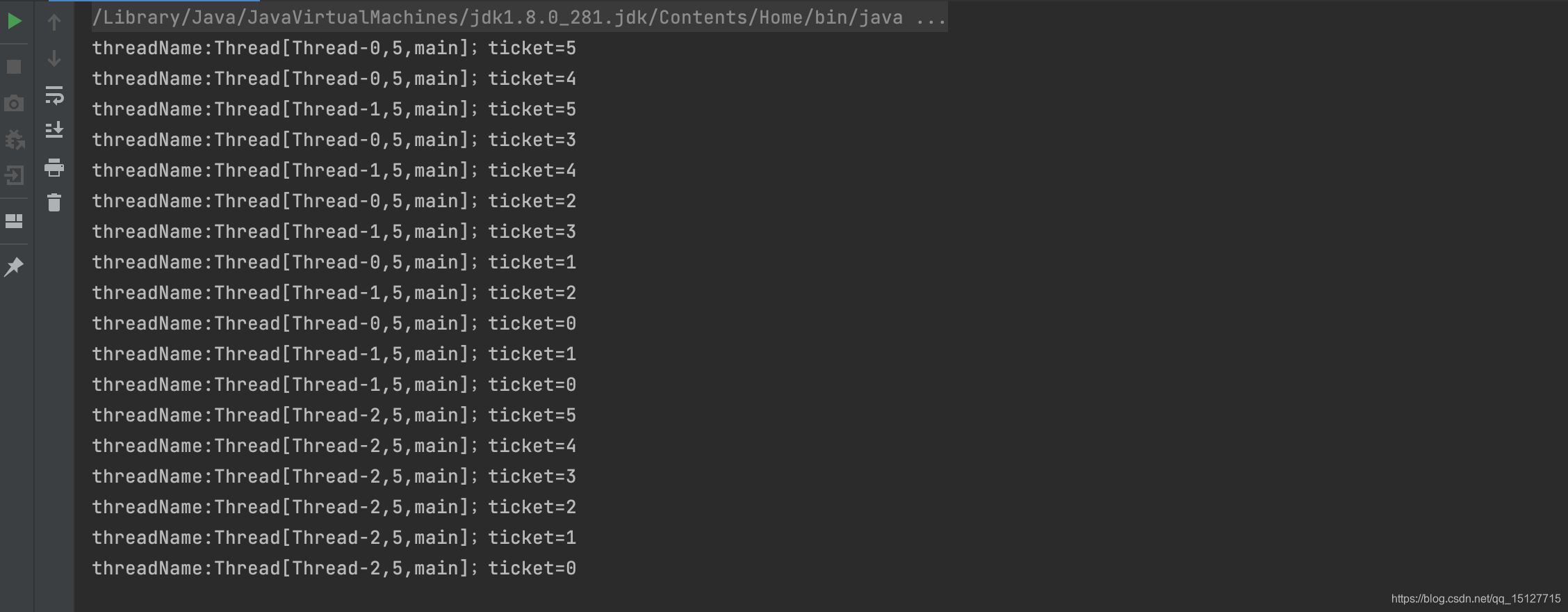
结果分析:从下图输出结果中可以分析，使用继承Thread类实现卖票，导致每个窗口都卖了五张票，而这个电影院总共才五张票，多线程出现了超卖现象。原因是继承Thread方式,是多线程多实例，无法实现资源的共享。

2.3多线程卖票小程序优化

在2.2的小程序案列中，我们发现了在多线程的环境下, 由于公共资源可能会被多个线程共享, 也就是多个线程可能会操作同一资源. 当多个线程操作同一块资源时, 很容易导致数据错乱或发生数据安全问题,
即: 数据有可能丢失, 有可能增加, 有可能错乱.

我们如何避免这种现象呢？具体看代码:

package trhead;/*** @author  cy* @date  2021-06-09*@deprecated  Runnable实现多线程卖票*/
public class TicketRunnableDemoTest {//设置票数private  static int ticket = 5;public static void main(String[] args) {//新建两个线程RunnableDemoTest1 r =  new RunnableDemoTest1();new Thread(r).start();new  Thread(r).start();}/*** 通过runnable 方式实现多线程*/
static class  RunnableDemoTest1  implements  Runnable{@Overridepublic void run() {while (ticket > 0){saleTicket();}}/*** 实现卖票方法*/public  void  saleTicket(){if(ticket>0){System.out.println("threadName:"+Thread.currentThread()+ "正在出票，余票剩余:"+ticket-- +"张");}}
}
}

结果分析:从下图输出结果中可以分析，实现Runnable接口进行卖票，电影院总共才五张票，多线程卖票正常。原因是实现Runnable方式，是多线程单实例，可实现资源的共享。

2.4多线程卖票小程序优化升级

细心的小伙伴可能会发现，怎么在2.3输出打印的票数不是从大到小排序的，这跟现实中的卖票场景不一样呐。如果想解决这样的问题,就必须使用同步,所谓的同步就是指多个操作在同一个时间段内只有一个线程进行,其他线程要等待此线程完成之后才可以继续执行。
下面我们通过对2.3代码进行继续优化，实现真实卖票场景。

 /**
* 通过synchronized实现线程同步* 实现卖票方法*/ public synchronized   void   saleTicket1(){if(ticket>0){System.out.println("threadName:"+Thread.currentThread()+ "正在出票，余票剩余:"+ +ticket-- +"张");}}

结果分析:从下图输出结果中可以分析，通过同步代码的方法进行代码的加锁操作，实现了卖票场景。

---

总结

这节主要给大家介绍了多线程的实现以及相应的一些使用场景，并且引入了同步的知识点，下一节主要介绍synchronized关键字的使用。
另外，码字不容易，如果发现小编描述有误，麻烦指摘。