文章目录
- 状态方程和输出方程
- 基本的状态空间方程
- 线性非线性时变时不变
- 系统的能控能观
- 状态方程的解
- 无输入线性时不变
- 转移矩阵
- 拉普拉斯求转移矩阵
- 有输入线性时不变
控制什么?
输入u1,u2,u3,…输出y1,y2,y3…的系统。u是控制量,y是响应结果,也可以被反馈测量到。
状态方程和输出方程
基本的状态空间方程
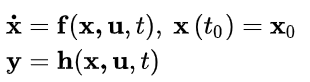
第一行是状态方程,第二行是输出方程。
首先x是状态变量。一个x就是系统的一个状态。但也不能随便找系统中一个变量就都当作状态,找来做状态变量的状态,它的初值一定要与输出量y密切相关。看起来,状态变量像是系统的中间量。但实际上它的初值能够决定输出。简单来说,系统的输出与输入以及状态变量初值有关。
比如一个LRC电路,R的电压可以测量,想把它作为输出,输入当然就是电源电压u。至于状态变量,我们都知道,该电路的状态与电源电压u,电容电压初值uc,电感电流初值il有关,那便把uc,iL作为状态变量,这些东西已经足够描述这个电路了。至于电感电压,电容电流这些东西就不重要了。
系统由状态变量描述。状态变量由输入以及状态变量自己的初值决定。输出可以根据需求随便选。
线性非线性时变时不变
方程能写成下面这样就是线性系统:当然下面这些A,B,C,D矩阵都是可以随时间变化的。
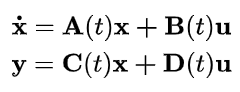
假设有两个状态变量,拿一个状态变量来举例子,比如x1,当系统线性时,x1的微分可以拿x1,x2,u1,u2的线性组合来表示,而不是 x 1 2 , e x 1 x^2_1, e^{x_1} x12,ex1,这种怪东西的组合来表示。
线性时不变就是上面的A,B,C,D不随时间变化。
非线性时变系统:
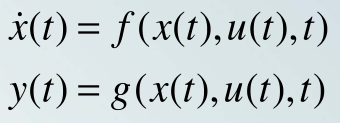
系统的能控能观
能控:输入量能控状态变量
能观:通过看输出量可以知道状态变量
由此可见,系统的核心是状态变量。
状态方程的解
要求解这个:
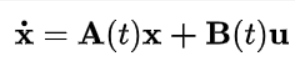
无输入线性时不变
转移矩阵
无输入线性时不变的状态方程为:
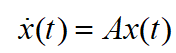
如果只有一个状态变量,便很容易求解:
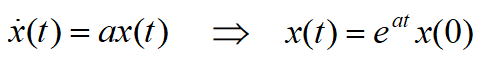
e a t e^{at} eat泰勒展开:
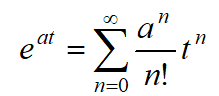
把里面的a改成矩阵A,并假设改之后的展开式为 e A t e^{At} eAt
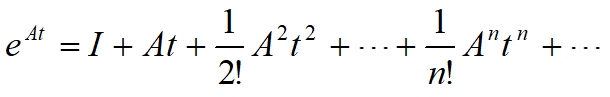
把右边的展开式乘以x(0)后代入原状态方程中,发现是符合的,那就说明所谓的“ e A t x ( 0 ) e^{At}x(0) eAtx(0)”就是状态方程的解。
用一个转移矩阵和状态变量初值来表示状态方程的解:尤其注意所谓的 e A t e^{At} eAt是个临时定义的东西。
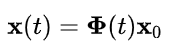
而且:
Φ ( t ) = e A t \Phi (t)=e^{At} Φ(t)=eAt
拉普拉斯求转移矩阵
上面的 e A t e^{At} eAt是个一长串的东西,根本写不出来,要求转移矩阵的话要还是得用拉普拉斯表示。
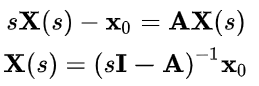
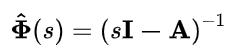
求出来转移矩阵的拉普拉斯形式后,再反变换即可。
有输入线性时不变
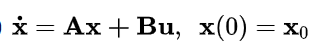
首先直接拉式变换:
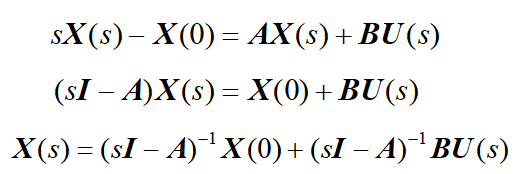
反变换:
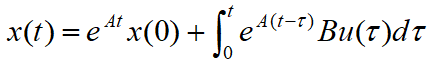
第一项就是转移矩阵,齐次解;第二项是转移矩阵的拉普拉斯变换与输入量拉普拉斯相乘,在时域上就是卷积,特解。
求解的时候,首先应该知道转移矩阵的时域形式(用上一节的方法),然后按照上面的式子卷积。
输出方程的解:
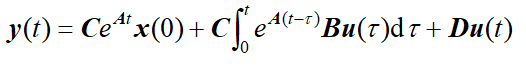
第一项是零输入响应,后面两个是零状态响应。
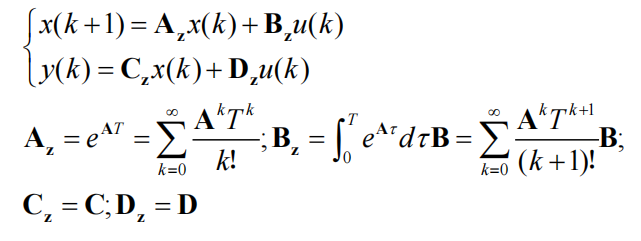

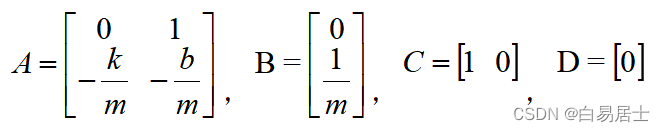
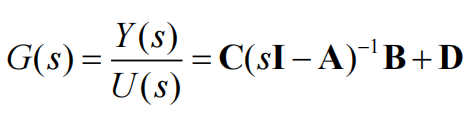






![[译]理解PG如何执行一个查询-1](https://img-blog.csdnimg.cn/img_convert/10d0b27d31ad7923560b0962e18f6392.png)