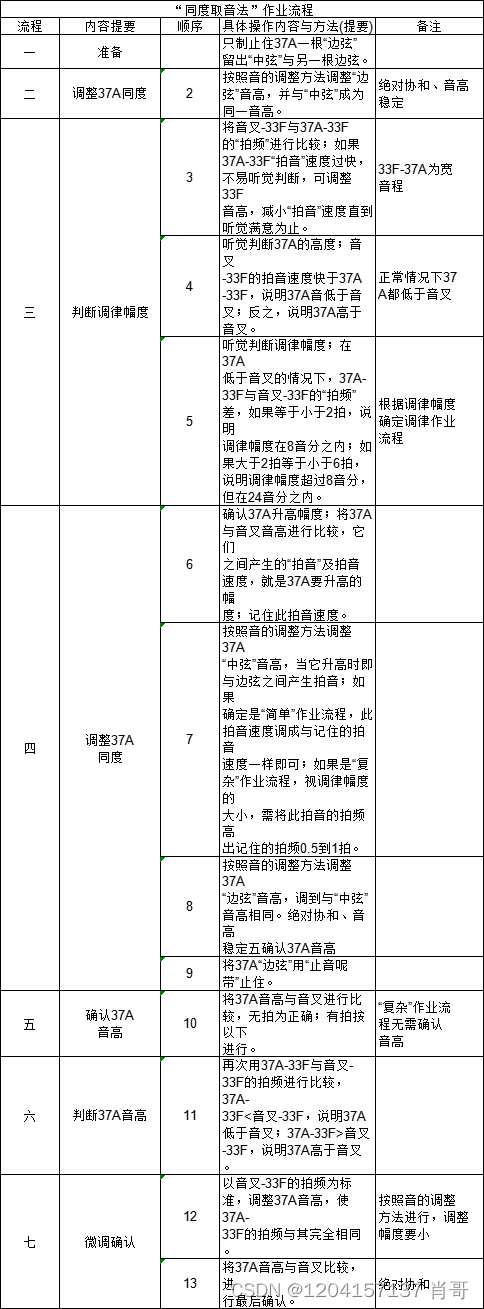
数据融合 协方差 状态空间方程 观测器
- 一、数据融合
- 假设举例
- 公式推导过程
- 再次理解
- 二、状态空间方程
- 阻尼滑块模型
- 1、连续表达式
- 2、离散表达形式
- 3、符号含义
- 参考文献
一、数据融合
假设举例
假设测量一物体的质量,现在有两个测量设备但是都存在误差且误差服从正态分布,分别用两个设备进行测量第一设备测量的测量值为 z 1 z_1 z1 ,标准差为 σ 1 \sigma_1 σ1;第二设备测量的测量值为 z 2 z_2 z2 ,标准差为 σ 2 \sigma_2 σ2 。现在有两个测量值那么应该更愿意去相信那个设备测出的值呢?或者把两次数据进行处理导出一个更接近真实值的值呢?
如果已知: z 1 = 30 g ; σ 1 = 2 g z_1=30g;\sigma_1=2g z1=30g;σ1=2g
z 2 = 32 g ; σ 2 = 4 g z_2=32g;\sigma_2=4g z2=32g;σ2=4g
现在让估算真实值,该如何计算呢?
分析:显而易见最终所估算的真实值也是服从正态分布的,且其结果在 z 1 z_1 z1 z 2 z_2 z2之间,由于标准差 σ 1 比 σ 2 \sigma_1比\sigma_2 σ1比σ2小则更靠近 z 1 z_1 z1。
公式推导过程
通过上一博客可知:当前的估计值 = 上一次的估计值 + 系数 (当前测量值 - 上一次的估计值)Kalman Filtering通过调整观测值和估计值的权重,使修正后的值更趋向于相信观测值还是相信估计值的一个过程。当我们使用同一设备进行测量时估计值通常是进行数学建模计算得出,由于有的误差无法建模所以得出的值只能是估计值,如第一篇博客所举的例子中当前估计值与上一次估计值分别是第 K K K次取平均值和第 K − 1 K-1 K−1次取平均值,而当前测量值为第 K K K次测量结果。从这我们也可以看出数据融合的思想,数学建模值与测量值之间融合得到最接近真实值的结果。但是本博客举得例子是两个设备测量结果没有进行建模,应该如何使用Kalman Filtering?其实同理只需要将一个值作为数学建模的结果即估计值,另一个作为测量结果即可。所以Kalman Filtering的数据融合是两个值之间的融合,不论值是建模得来还是传感器测得都行。
现在要得出一个最优估计值 z ^ \hat{z} z^,由以上面推导的公式可知:(将 z 1 z_1 z1当作估计值; z 2 z_2 z2当作测量值)
z ^ = z 1 + K ( z 2 − z 1 ) (1) \hat{z}=z_{1}+K\left(z_{2}-z_{1}\right)\tag1 z^=z1+K(z2−z1)(1)
式中 : K ⟶ : K \longrightarrow :K⟶ 卡尔曼增益/因数, 且 K ∈ [ 0 , 1 ] K \in[0,1] K∈[0,1] 。
K = 0 K=0 K=0 ⇒ \Rightarrow ⇒ z ^ = z 1 \hat{z}=z_{1} z^=z1
K = 1 K=1 K=1 ⇒ \Rightarrow ⇒ z ^ = z 2 \hat{z}=z_{2} z^=z2
现在目标是求 K K K 使得 σ z ^ \sigma_{\hat{z}} σz^ 最小 ⇒ \Rightarrow ⇒ 求 K K K 使得方差 Var ( z ^ ) \operatorname{Var}(\hat{z}) Var(z^) 最小 ⇒ \Rightarrow ⇒ 求 K K K使误差最小。
则:
σ z ^ 2 = V ar ( z 1 + K ( z 2 − z 1 ) ) = V ar ( z 1 − K z 1 + K z 2 ) = V ar ( ( 1 − K ) z 1 + K z 2 ) ⟶ 两 个 设 备 测 量 结 果 与 误 差 , 相 互 独 立 , 互 不 影 响 = Var ( ( 1 − K ) z 1 ) + Var ( K z 2 ) ⟶ K 为 常 数 , 从 方 差 中 提 出 得 带 平 方 = ( 1 − K ) 2 Var ( z 1 ) + K 2 Var ( z 2 ) = ( 1 − K ) 2 σ 1 2 + K 2 σ 2 2 \begin{aligned} \sigma_{\hat{z}}^{2} &=\boldsymbol{V} \operatorname{ar}\left(z_{1}+K\left(z_{2}-z_{1}\right)\right) \\ &=\boldsymbol{V} \operatorname{ar}\left(z_{1}-K z_{1}+K z_{2}\right) \\ &=\boldsymbol{V} \operatorname{ar}\left((1-K) z_{1}+K z_{2}\right) \longrightarrow两个设备测量结果与误差,相互独立,互不影响\\ &=\operatorname{Var}\left((1-K) z_{1}\right)+\operatorname{Var}\left(K z_{2}\right) \longrightarrow K为常数,从方差中提出得带平方\\ &=(1-K)^{2} \operatorname{Var}\left(z_{1}\right)+K^{2} \operatorname{Var}\left(z_{2}\right) \\ &=(1-K)^{2} \sigma_{1}^{2}+K^{2} \sigma_{2}^{2} \end{aligned} σz^2=Var(z1+K(z2−z1))=Var(z1−Kz1+Kz2)=Var((1−K)z1+Kz2)⟶两个设备测量结果与误差,相互独立,互不影响=Var((1−K)z1)+Var(Kz2)⟶K为常数,从方差中提出得带平方=(1−K)2Var(z1)+K2Var(z2)=(1−K)2σ12+K2σ22
求方差最小值时,则方差 σ ı ^ 2 \sigma_{\hat{\imath}}^{2} σı^2 对 K K K 的导数为零,即:
∂ σ z ^ 2 ∂ K = 0 ⇒ − 2 ( 1 − K ) σ 1 2 + 2 K σ 2 2 = 0 ⇒ − σ 1 2 + K σ 1 2 + K σ 2 2 = 0 ⇒ K ( σ 1 2 + σ 2 2 ) = σ 1 2 ⇒ K = σ 1 2 σ 1 2 + σ 2 2 \begin{aligned} \frac{\partial \sigma_{\hat{z}}^{2}}{\partial K}=0 & \Rightarrow-2(1-K) \sigma_{1}^{2}+2 K \sigma_{2}^{2}=0 \\ & \Rightarrow-\sigma_{1}^2+K \sigma_{1}^{2}+K \sigma_{2}^{2}=0 \\ & \Rightarrow K\left(\sigma_{1}^{2}+\sigma_{2}^{2}\right)=\sigma_{1}^{2} \\ & \Rightarrow K=\frac{\sigma_{1}^{2}}{\sigma_{1}^{2}+\sigma_{2}^{2}} \end{aligned} ∂K∂σz^2=0⇒−2(1−K)σ12+2Kσ22=0⇒−σ12+Kσ12+Kσ22=0⇒K(σ12+σ22)=σ12⇒K=σ12+σ22σ12
可以看出K的取值与进行数据融合的两个值的误差大小有关:
当 σ 2 > > σ 1 \sigma_{2}>>\sigma_{1} σ2>>σ1时 K = 0 K=0 K=0 ⇒ \Rightarrow ⇒ z ^ = z 1 \hat{z}=z_{1} z^=z1
当 σ 2 < < σ 1 \sigma_{2}<<\sigma_{1} σ2<<σ1时 K = 1 K=1 K=1 ⇒ \Rightarrow ⇒ z ^ = z 2 \hat{z}=z_{2} z^=z2
σ 1 = 2 g ; σ 2 = 4 g \sigma_1=2g;\sigma_2=4g σ1=2g;σ2=4g带入数据得: K = 0.2 K=0.2 K=0.2带入(1)式中得 z ^ = 30.4 g \hat{z}=30.4g z^=30.4g
σ z ^ 2 = 3.2 ⇒ σ z ^ = 1.79 < m i n [ σ 1 2 , σ 2 2 ] \sigma_{\hat{z}}^{2}=3.2 \Rightarrow \sigma_{\hat{z}}=1.79<min{[\sigma_1^2,\sigma_2^2]} σz^2=3.2⇒σz^=1.79<min[σ12,σ22]
上面所进行的过程就是数据融合的过程,由此可见将两个设备所测得的数据进行融合所得到的误差更小更加接近真实值。卡尔曼滤波利用信息融合减少误差从而使估计值更加接近真实值也就是寻找最优估计得过程。
再次理解
现在可以看出卡尔曼滤波信息融合的关键就是要求卡尔曼增益 K K K,这个就是一个权值使当前估计值趋近于误差小的估计值。上面通过严谨的数学公式推导得出了估计值 z ^ = 30.4 g \hat{z}=30.4g z^=30.4g,下面用小学二年级的知识在来理解理解:
已知: z 1 = 30 g ; σ 1 = 2 g z_1=30g;\sigma_1=2g z1=30g;σ1=2g
z 2 = 32 g ; σ 2 = 4 g z_2=32g;\sigma_2=4g z2=32g;σ2=4g
解:
加权平均值
z ^ = z 1 σ 2 2 σ 1 2 + σ 2 2 + z 2 σ 1 2 σ 1 2 + σ 2 2 = 30 × 4 2 2 2 + 4 2 + 32 × 2 2 2 2 + 4 2 = 30.4 \begin{aligned} \hat{z}&=z_1\frac{\sigma _2^2}{\sigma _1^2+\sigma _2^2} +z_2\frac{\sigma _1^2}{\sigma _1^2+\sigma _2^2}\\ &=30\times\frac{4^2}{2^2+4^2} + 32\times\frac{2^2}{2^2+4^2} \\ &=30.4 \end{aligned} z^=z1σ12+σ22σ22+z2σ12+σ22σ12=30×22+4242+32×22+4222=30.4
两个设备测量的结果不相关,相互独立,则两个的加权平均值就为 z ^ \hat{z} z^。其中误差小的测量结果乘以权重大的;反之误差大的测量结果乘以权重小的;很好理解因为我们是比较相信误差小的结果的。
由于两个测量误差不相关则:(可以理解为并联电阻)
1 σ z ^ 2 = 1 σ 1 2 + 1 σ 2 2 = 1 2 2 + 1 4 2 = 0.3125 ⇒ σ z ^ 2 = 3.2 ⇒ σ z ^ = 1.79 \begin{aligned} \frac{1}{\sigma _{\hat{z} }^2} &=\frac{1}{\sigma _{1 }^2}+\frac{1}{\sigma _{2 }^2}\\ &=\frac{1}{2^2}+\frac{1}{4^2}\\ &=0.3125\\ \Rightarrow \sigma _{\hat{z} }^2&=3.2\Rightarrow\sigma _{\hat{z} }=1.79 \end{aligned} σz^21⇒σz^2=σ121+σ221=221+421=0.3125=3.2⇒σz^=1.79
如果误差相关误差相关则为: σ z ^ 2 = σ 1 2 + σ 2 2 \sigma _{\hat{z}}^2 = \sigma _{{1}}^2 + \sigma _{{2} }^2 σz^2=σ12+σ22(串联电阻)
一般情况下:串联误差为误差相关;
并联误差为误差不相关。
二、状态空间方程
系统会有一系列的状态,这个状态你可以任意的去选择,只要你觉得能够充分表达你所需要的信息。系统状态会发生变化,那么这个变化应当和什么有关呢?
- 系统当前的状态;
- 系统的输入。
阻尼滑块模型
一个弹簧滑块系统,滑块的加速度(受到的外力)和系统当前的位置有关(弹簧弹力),也和外力输入有关(人手或电机给与滑块一个外力)。将输入记为u。系统状态的变化,对于连续系统而言,是系统的导数,对于离散系统而言,是系统状态的变化量,一般取为系统下一时刻的状态( x k + 1 \boldsymbol{x}_{k+1} xk+1= A x k + B u k \boldsymbol{A} \boldsymbol{x}_{k}+B u_{k} Axk+Buk),二者包含的信息一致。

系统的输出和什么有关呢?当然是和系统当前状态和输入有关。
1、连续表达式
该系统动态方程表达式为:
m x ¨ + c x ˙ + k x = F m \ddot{x}+c \dot{x}+k x=F mx¨+cx˙+kx=F
令 x 1 = x , x 2 = x ˙ , u = F x_{1}=x, x_{2}=\dot{x}, u=F x1=x,x2=x˙,u=F, 有
x ˙ 1 = x 2 x ˙ 2 = x ¨ = 1 m u − c m x ˙ − k m x = 1 m u − c m x 2 − k m x 1 \begin{gathered} \dot{x}_{1}=x_{2} \\ \dot{x}_{2}=\ddot{x}=\frac{1}{m} u-\frac{c}{m} \dot{x}-\frac{k}{m} x \\ =\frac{1}{m} u-\frac{c}{m} x_{2}-\frac{k}{m} x_{1} \end{gathered} x˙1=x2x˙2=x¨=m1u−mcx˙−mkx=m1u−mcx2−mkx1
假设位置测量量为 z 1 = x = x 1 z_{1}=x=x_{1} z1=x=x1, 速度测量量为 z 2 = x ˙ = x 2 z_{2}=\dot{x}=x_{2} z2=x˙=x2,将上式用矩阵形式表达则有:
[ x ˙ 1 x ˙ 2 ] = [ 0 1 − k m − c m ] [ x 1 x 2 ] + [ 0 1 m ] u \begin{aligned} \left[\begin{array}{c} \dot{x}_{1} \\ \dot{x}_{2} \end{array}\right]=\left[\begin{array}{cc} 0 & 1 \\ -\frac{k}{m} & -\frac{c}{m} \end{array}\right]\left[\begin{array}{l} x_{1} \\ x_{2} \end{array}\right]+\left[\begin{array}{c} 0 \\ \frac{1}{m} \end{array}\right] u \end{aligned} [x˙1x˙2]=[0−mk1−mc][x1x2]+[0m1]u
[ z 1 z 2 ] = [ 1 0 0 1 ] [ x 1 x 2 ] \begin{aligned} \left[\begin{array}{l} z_{1} \\ z_{2} \end{array}\right]=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x_{1} \\ x_{2} \end{array}\right] \end{aligned} [z1z2]=[1001][x1x2]
上述表达形式即状态空间表达形式,上述表达式可分别归纳为随时间变化表达式:
x ˙ ( t ) = A x ( t ) + B u ( t ) z ( t ) = H x ( t ) \begin{gathered} \dot{\boldsymbol{x}}(t)=A \boldsymbol{x}(t)+B u(t) \\ \boldsymbol{z}(t)=H \boldsymbol{x}(t) \end{gathered} x˙(t)=Ax(t)+Bu(t)z(t)=Hx(t)
2、离散表达形式
x k = A x k − 1 + B u k − 1 z k = H x k \begin{gathered} \boldsymbol{x}_{k}=\boldsymbol{A} \boldsymbol{x}_{k-1}+B u_{k-1} \\ \boldsymbol{z}_{k}=H \boldsymbol{x}_{k} \end{gathered} xk=Axk−1+Buk−1zk=Hxk
其中,下标 k 、 k − 1 、 k + 1 k、 k-1、k+1 k、k−1、k+1 表示采样时间。即系统当前状态与系统上一时刻状态和上一时刻输入有关。
由于所有的系统数学模型往往是理想模型,存在许多假设,与实际模型存在差距。比如上述阻尼滑块模型表达式中就忽略了阻力的存在即系统存在噪声且噪声的表达式未知,所以应当加入未知噪声时表达式为:
x k = A x k − 1 + B u k − 1 + w k − 1 z k = H x k + v k \begin{gathered} \boldsymbol{x}_{k}=\boldsymbol{A} \boldsymbol{x}_{k-1}+B u_{k-1}+\boldsymbol{w}_{k-1} \\ \boldsymbol{z}_{k}=H \boldsymbol{x}_{k}+\boldsymbol{v}_{k} \end{gathered} xk=Axk−1+Buk−1+wk−1zk=Hxk+vk
其中: w ⟶ w \longrightarrow w⟶ 过程噪音
v ⟶ v \longrightarrow v⟶ 测量噪音
卡尔曼滤波器的目的即从存在噪声的数据中求出误差最小的结果。
3、符号含义
| 符号 | 意义 | 备注 |
|---|---|---|
| x k x_{k} xk | 系统状态矩阵(真实值) | 计算得到 |
| z k z_{k} zk | 状态阵的观测量 | 实际测量 |
| A A A | 状态转移矩阵 | – |
| B B B | 控制输入矩阵 | – |
| H H H | 状态观测矩阵 | – |
| w k − 1 w_{k-1} wk−1 | 过程噪声 | 服从正态分布 |
| v k v_{k} vk | 测量噪声 | 服从正态分布 |
参考文献
DR_CAN
【官方教程】卡尔曼滤波器教程与MATLAB仿真(全)(中英字幕)
![[现代控制理论]2_state-space状态空间方程](https://img-blog.csdnimg.cn/06f8faa0b32a4ae88802d588d3e85463.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA6LWw5bGx5YGc5rC0,size_20,color_FFFFFF,t_70,g_se,x_16)
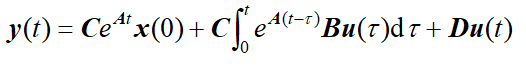
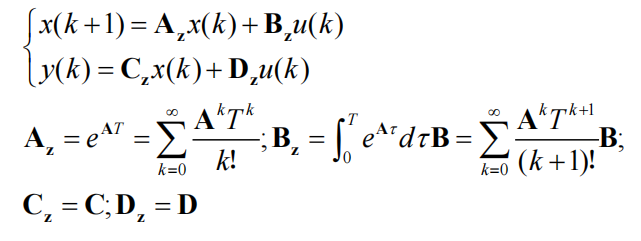

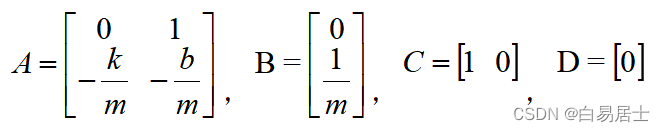






![[译]理解PG如何执行一个查询-1](https://img-blog.csdnimg.cn/img_convert/10d0b27d31ad7923560b0962e18f6392.png)

