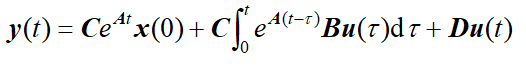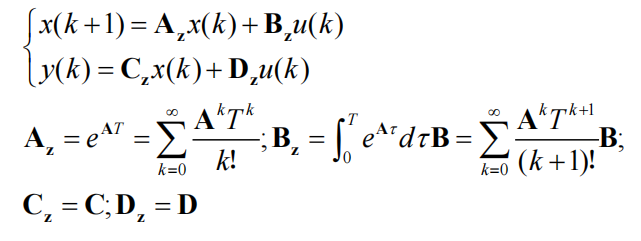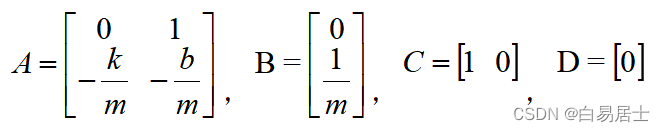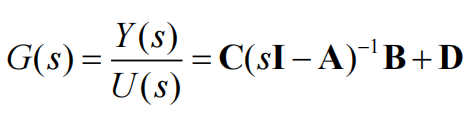1、传递函数
1.1 构造传递函数
(1)
Matlab可以这样构造上式
num=[10 30 20];
den=[1 12 47 60];
sysc=tf(num,den)(2)
根据零极点构造表达式:
z=[-1 -2];
p=[-3 -4 -5];
k=10;
sysc=zpk(z,p,k)(3)多项式表达式和零极点表达式之间的转化
已有
num=[10 30 20];den=[1 12 47 60];sysc_tf=tf(num,den);
z=[-1;-2];p=[-3;-4;-5];k=10;sysc_zpk=zpk(z,p,k);i 多项式转化为零极点形式:
sysc_tf1=tf(sysc_zpk)或者
[z1,p1,k1]=tf2zp(num,den);
sysc_zpk=zpk(z1,p1,k1)结果都是
ii零极点转化为多项式形式:
sysc_tf=tf(sysc_zpk)或者
[num1,den1]=zp2tf(z,p,k);
sysc_tf=tf(num1,den1)结果都是
(4)
构造下式所示的传递函数
可以:
num=[5];
den=[1 10 0];
g=tf(num,den,'ioDelay',3)也可以
z=[];
p=[0 -10];
k=1;
g2=zpk(z,p,k,'ioDelay',3)1.2 传递函数串联、并联、反馈
num1=[1 2];den1=[3 4];G1=tf(num1,den1);
num2=[1 2];den2=[3 4];G2=tf(num2,den2);1.2.1串联
G3=series(G1,G2)或者
[num3,den3]=series(num1,den1,num2,den2);
G3=tf(num3,den3)1.2.2并联
G3=parallel(G1,G2)或者
[num3,den3]=parallel(num1,den1,num2,den2);
G3=tf(num3,den3)G3=feedback(G1,G2)或者
[num3,den3]=feedback(num1,den1,num2,den2);
G3=tf(num3,den3)feedback(G,H)。其中G是传递函数,H为反馈函数,表示一个控制系统G,对其进行负反馈H(要求正反馈用-H)。
2、z传递函数
2.1 z传递函数的构造
num=[1 2];
den=[1 2 3];
G=tf(num,den,1)%采样时间为1s结果:
或者可以这样
z=tf('z',1);
G=(z+2)/(z^2+2*z+3)结果也是
2.2 z传递函数和传递函数的转化
z函数转化为s函数
num=[1 2];den=[1 2 3];G=tf(num,den,1);%采样时间为1s
csysc=d2c(G)
[num, den] = tfdata( csys, 'v' )%获取s函数分子、分母结果
s函数转化为z函数
紧接上式
Hd=c2d(csysc,1,'zoh')得到结果
3、状态空间函数
3.1构造状态空间函数
A=[0 1 -2;3 4 0; 5 0 0];
B=[0;1;0];
C=[0 0 1];
D=0;
sys=ss(A,B,C,D,1)3.2构造函数和传递函数的转化
A=[0 1 -2;3 4 0; 5 0 0];B=[0;1;0];C=[0 0 1];D=0;
%状态空间到传递函数
[num,den]=ss2tf(A,B,C,D)
%传递函数到状态空间
[A,B,C,D]=tf2ss(num,den)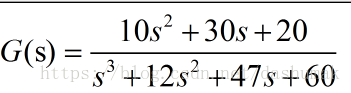

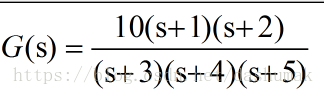
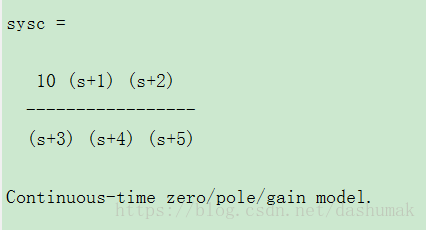












![[现代控制理论]2_state-space状态空间方程](https://img-blog.csdnimg.cn/06f8faa0b32a4ae88802d588d3e85463.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA6LWw5bGx5YGc5rC0,size_20,color_FFFFFF,t_70,g_se,x_16)