本文如有错误,恳请指正。
目录
离散系统
采样控制系统
数字控制系统
信号采样
采样定理(香农定理)
信号保持—零阶保持器
Z变换
Z 变换方法
级数求和法
部分分式法
基本定理
Z反变换
Z反变换方法
长除法
部分分式法(推荐)
差分方程
传递函数离散化
状态空间方程离散化
欧拉法
零阶保持法(推荐)
离散系统
离散系统:有一处或几处信号是脉冲序列或数码序列的控制系统。离散控制系统由连续的控制对象、离散的控制器、采样器和保持器等环节组成。
线性系统分为线性连续系统和线性离散系统,线性离散系统又分为采样控制系统和数字控制系统。
离散控制系统的优点:
- 校正装置效果比连续式校正装置好,软件实现控制规律控制灵活性高。
- 采样信号能有效地抑制噪声,系统抗干扰能力强。
- 可分时控制若干个系统,设备利用率高。
- 可实现复杂控制规律并且在运行中实时改变响应参数。
采样控制系统
采样控制系统:离散信号是脉冲序列(时间上离散、幅值上连续)形式的离散系统。
采样控制系统有两个特殊环节是采样器和保持器。
采样器(采样开关):把连续信号转变为脉冲序列的装置;
保持器:把脉冲序列转变为连续信号的实现信号恢复的装置。
数字控制系统
数字控制系统:离散信号是数码序列(时间和幅值都离散)形式的离散系统。
数字控制系统有两个重要环节是A/D转换器和D/A转换器。
A/D(模数转换器):相当于采样器,将连续的模拟信号转换为离散的数字信号,包括采样与量化两过程。
D/A(数模转换器):相当于保持器,将离散的数字信号转换为连续的模拟信号,包括解码与复现两过程。
信号采样
采样过程:连续信号经过采样器的采样变换成离散信号的过程。
采样周期:采样器经一定时间T,重复闭合,每次闭合时间为t,t<T,T称为采样周期。f=1/T为采样频率。
采样脉冲序列:连续时间函数经采样器采样后变成重复周期T的时间序列
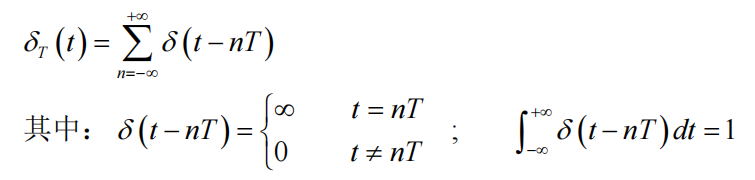
离散系统在开始采样后才有意义,所以当t<0时信号为0,离散信号表示为:
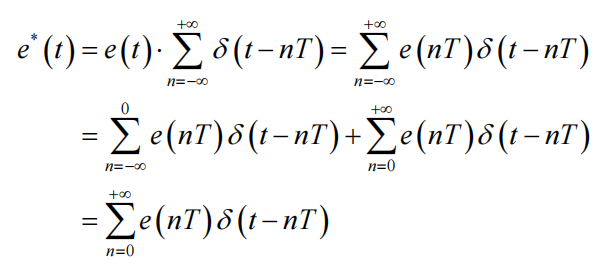
采样信号的拉氏变换为:
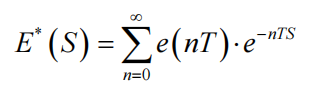
采样定理(香农定理)
连续信号的频谱是单一的连续频谱,其最大角频率为
![]()
采样信号的频谱则是以采样角频率为
![]()
周期的无穷多个频谱之和。
当
![]()
时,采样频谱中的补充分量相互交叠在一起,无法再恢复到原来的连续信号的频谱。
香农采样定理:当采样频率大于等于两倍的输入信号最高角频率才可能从采样信号中无失真地恢复出连续信号。
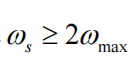
根据香农采样定理,采样周期T越小信息丢失内容越少,控制效果越好。采样周期不能过大,因为信息损失太多导致原信号不能准确恢复;采样周期T不能过小,因为会增加计算量和A/D及D/A转换器的字长,提高其运算与转换速度,增加系统实现成本。
在实际工程中,时域内,
![]()
频域内,
![]()
信号保持—零阶保持器
保持器具有低通滤波特性、相角滞后特性和时间滞后特性。使用保持器将数字信号转换复原成连续信号,保持器主要解决各采样时刻之间的插值问题,把具有恒值、线性和抛物线外推规律的保持器分别称为零阶、一阶和二阶保持器,其中最广泛应用零阶保持器。
零阶保持器的作用是将采样时刻t=kT的采样值f(kT)恒定不变的保持到下一个采样时刻(k+1)T,每个采样区间内的值为常数,导数为0,所以成为零阶保持器。零阶保持器的引入并不影响开环系统脉冲传递函数的极点。零阶保持器的数学表达式为
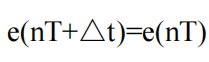
其脉冲响应为
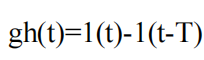
传递函数为:

Z变换
连续系统中,使用拉普拉斯变换把微分方程转换为代数方程。离散系统中,使用z变换把差分方程转换为代数方程。z变换本质上只能反映信号在采样时刻的值,而不能描述采样点间信号的状态,因此,不同的连续信号往往可能具有相同的z变换结果。
设连续信号f(t)的拉普拉斯变换为F(S),经过采样开关后的信号为f*(t),采样周期T,对其两边进行拉氏变换:
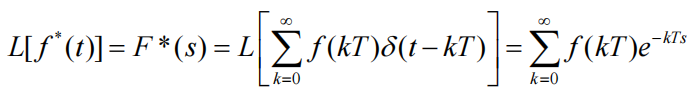
令
![]()
则 z 变换为

Z 变换方法
级数求和法
根据z变换定义求取,利用无穷级数求和公式计算。
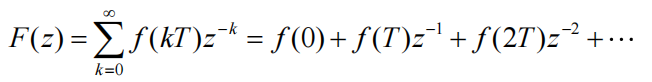
部分分式法
将连续函数f(t)的拉普拉斯变换F(s)极点展开成部分分式和的形式,其中p为F(s)的极点,A为系数,然后查z变换对照表求取。
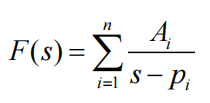
基本定理
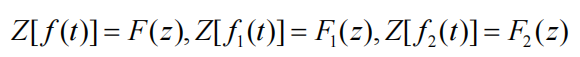
线性定理
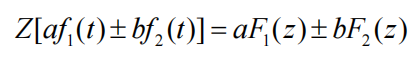
滞后定理(右偏移)
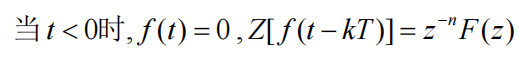
超前定理(左偏移)
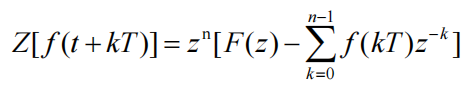
初值定理
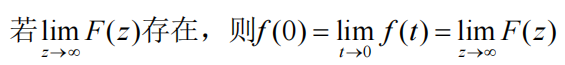
终值定理
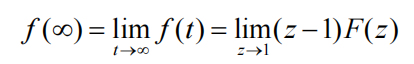
复平移定理
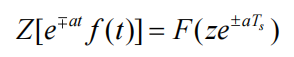
卷积定理
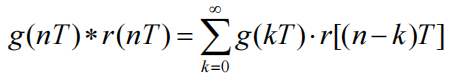
则卷积定理表示为
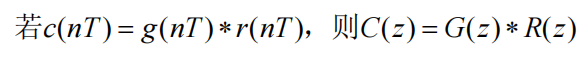
Z反变换
![]()
Z反变换方法
长除法
部分分式法(推荐)
差分方程
连续系统的动态过程采用拉普拉斯变换求解微分方程描述,离散系统的动态过程采用z变换求解差分方程描述。差分方程表示出系统离散输入与离散输出之间的函数关系。
一阶前向差分:
![]()
二阶前向差分:
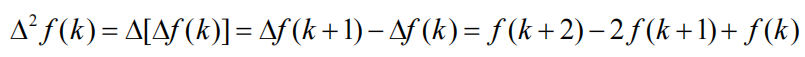
N 阶前向差分:
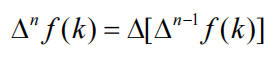
一阶后向差分:
![]()
二阶后向差分:

N 阶后向差分:
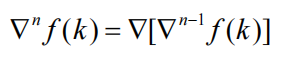
如果一个方程中除了含有函数本身外,还有函数的差分,称此方程为差分方程。差分方程的阶次为最高差分与最低差分之差。
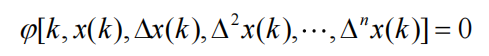
对于输入、输出均为离散信号的的线性定常离散系统,其线性定常差分方程为
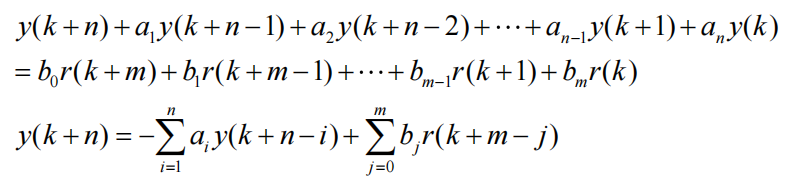
式中,r(k)为输入信号,y(k)为输出信号,an和bm 等均为常数。
传递函数离散化
将s域下的传递函数G(s)经过z变换将s变量全部替换为z得到G(z)。常用s域和z域的对应关系如下,T为采样时间
前向差分变换(嵌入式常用离散方法)
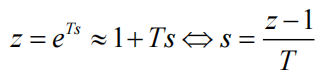
后向差分变换
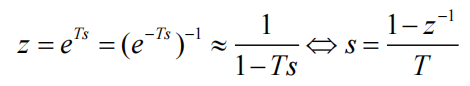
双线性变换(Tustin)
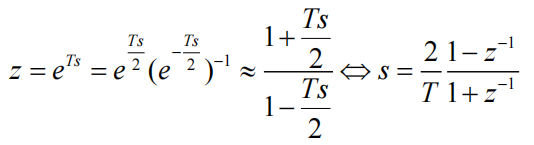
其他z变换方法可以使用Matlab进行计算,用 Matlab 对传递函数离散化的函数分为连续转为离散 c2d,离散转为连续d2c
Z变换转为差分方程
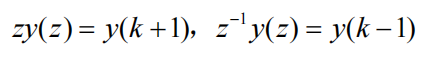
以连续系统的一阶传递函数为例,对其进行z变换离散化,然后写成差分方程的形式即可在嵌入式设备运行。
一阶传递函数,G(z)为连续系统输出与输入之比。
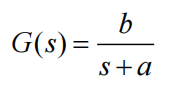
对一阶传递函数使用前向差分法离散化,G(z)为离散系统输出与输入之比。
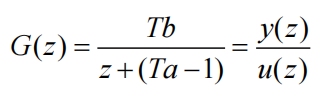
化简运算,将z变换写成差分方程形式,
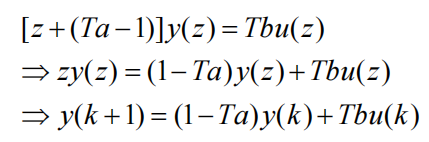
状态空间方程离散化
连续系统的状态空间方程表示为
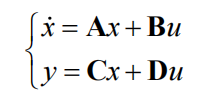
将状态空间方程离散化方法有欧拉法和零阶保持法等,本文介绍欧拉法和零阶保 持法,其中采样时间为 T。
欧拉法
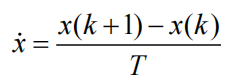
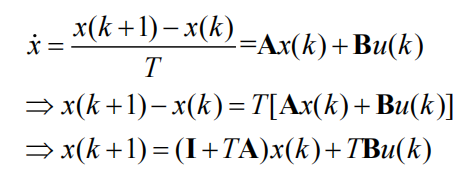
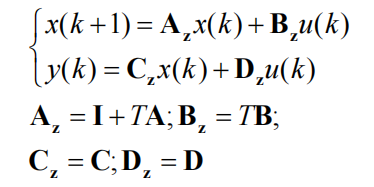
零阶保持法(推荐)
在连续系统的状态空间方程添加零阶保持器,然后一起Z变换离散化结合泰勒公式得到离散状态空间方程,其中离散状态空间方程的矩阵A和B的求解可以参照矩阵的一阶非齐次微分方程。
![]()
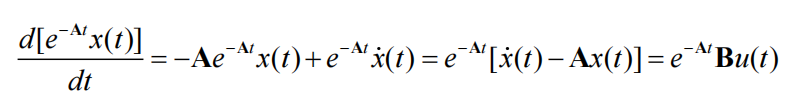
两边在[t0,t]上积分
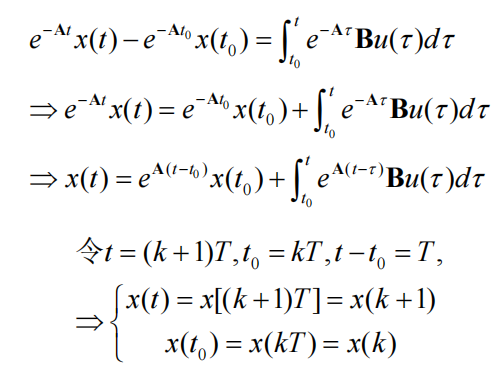
得到离散方程
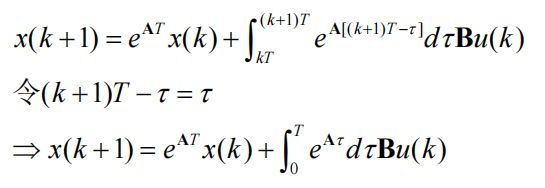
由泰勒公式得

最终得到离散状态空间方程
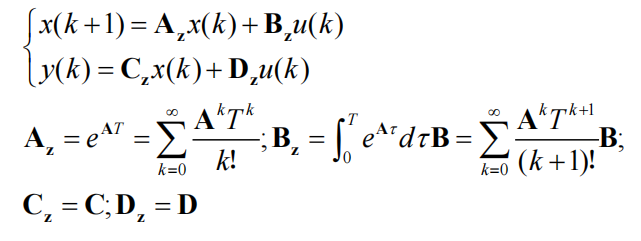

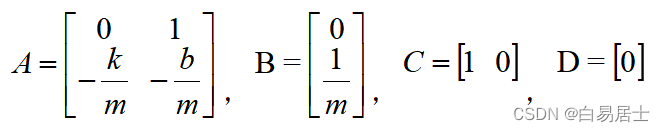
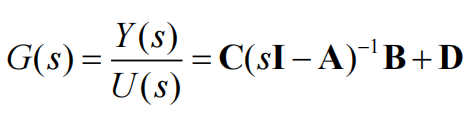






![[译]理解PG如何执行一个查询-1](https://img-blog.csdnimg.cn/img_convert/10d0b27d31ad7923560b0962e18f6392.png)